Jean-Marc Jicquel
EDF R&D TREE
New penalized criteria for smooth non-negative tensor factorization with missing entries
Mar 22, 2022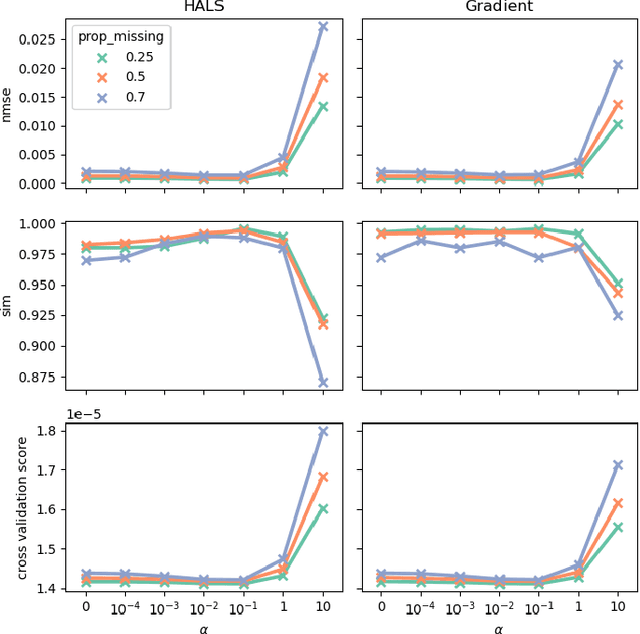
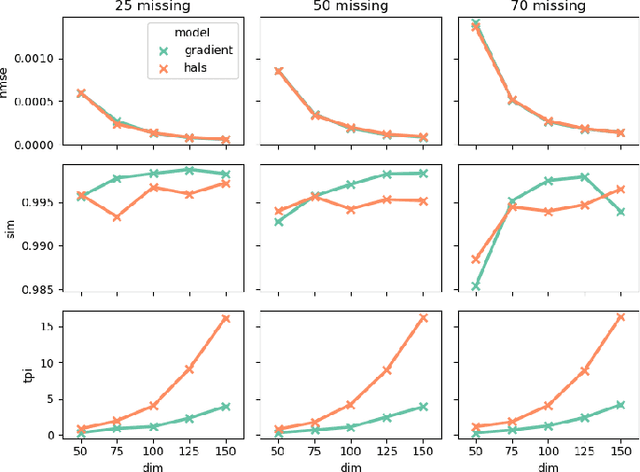
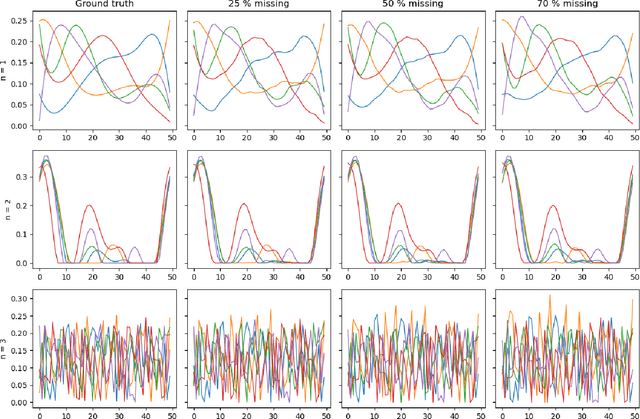
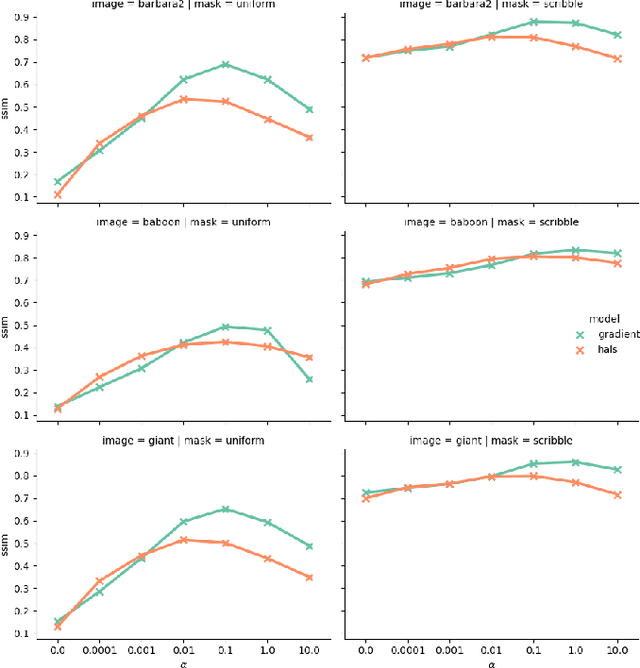
Abstract:Tensor factorization models are widely used in many applied fields such as chemometrics, psychometrics, computer vision or communication networks. Real life data collection is often subject to errors, resulting in missing data. Here we focus in understanding how this issue should be dealt with for nonnegative tensor factorization. We investigate several criteria used for non-negative tensor factorization in the case where some entries are missing. In particular we show how smoothness penalties can compensate the presence of missing values in order to ensure the existence of an optimum. This lead us to propose new criteria with efficient numerical optimization algorithms. Numerical experiments are conducted to support our claims.
Smooth nonnegative tensor factorization for multi-sites electrical load monitoring
Mar 12, 2021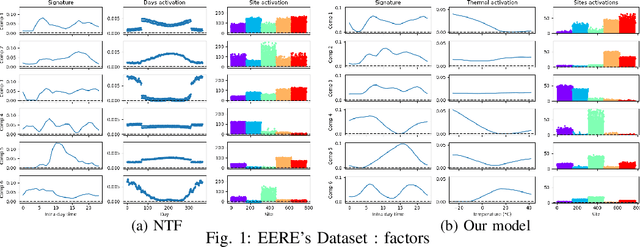
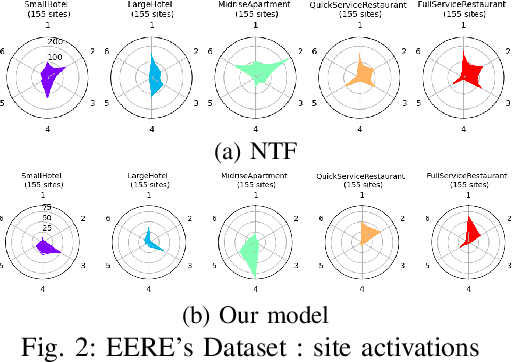
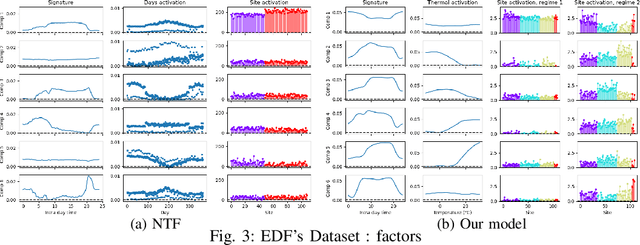
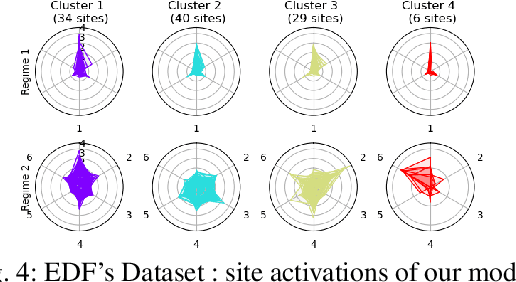
Abstract:The analysis of load curves collected from smart meters is a key step for many energy management tasks ranging from consumption forecasting to customers characterization and load monitoring. In this contribution, we propose a model based on a functional formulation of nonnegative tensor factorization and derive updates for the corresponding optimization problem. We show on the concrete example of multi-sites load curves disaggregation how this formulation is helpful for 1) exhibiting smooth intraday consumption patterns and 2) taking into account external variables such as the outside temperature. The benefits are demonstrated on simulated and real data by exhibiting a meaningful clustering of the observed sites based on the obtained decomposition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge