Variational Diffusion Posterior Sampling with Midpoint Guidance
Paper and Code
Oct 13, 2024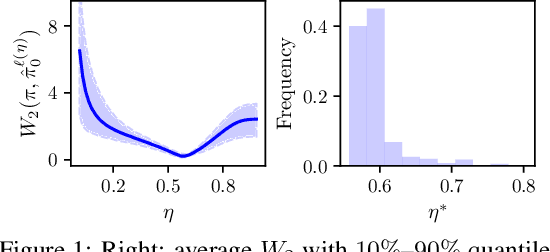
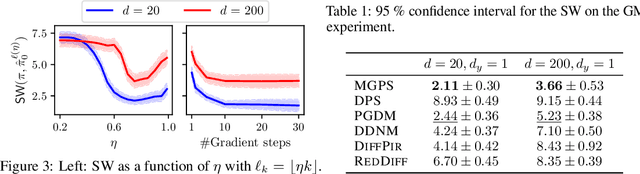

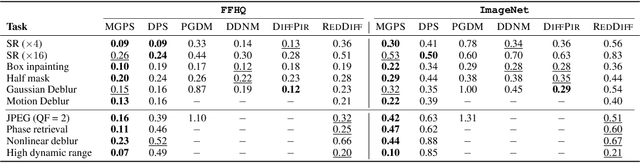
Diffusion models have recently shown considerable potential in solving Bayesian inverse problems when used as priors. However, sampling from the resulting denoising posterior distributions remains a challenge as it involves intractable terms. To tackle this issue, state-of-the-art approaches formulate the problem as that of sampling from a surrogate diffusion model targeting the posterior and decompose its scores into two terms: the prior score and an intractable guidance term. While the former is replaced by the pre-trained score of the considered diffusion model, the guidance term has to be estimated. In this paper, we propose a novel approach that utilises a decomposition of the transitions which, in contrast to previous methods, allows a trade-off between the complexity of the intractable guidance term and that of the prior transitions. We validate the proposed approach through extensive experiments on linear and nonlinear inverse problems, including challenging cases with latent diffusion models as priors, and demonstrate its effectiveness in reconstructing electrocardiogram (ECG) from partial measurements for accurate cardiac diagnosis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge