BR-SNIS: Bias Reduced Self-Normalized Importance Sampling

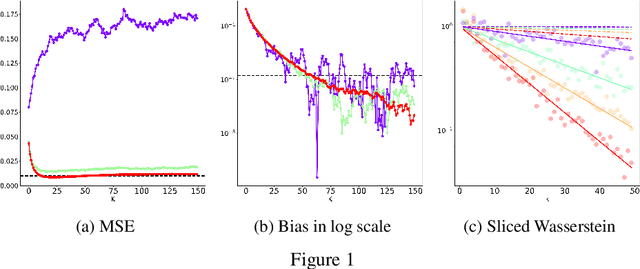
Importance Sampling (IS) is a method for approximating expectations under a target distribution using independent samples from a proposal distribution and the associated importance weights. In many applications, the target distribution is known only up to a normalization constant, in which case self-normalized IS (SNIS) can be used. While the use of self-normalization can have a positive effect on the dispersion of the estimator, it introduces bias. In this work, we propose a new method, BR-SNIS, whose complexity is essentially the same as that of SNIS and which significantly reduces bias without increasing the variance. This method is a wrapper in the sense that it uses the same proposal samples and importance weights as SNIS, but makes clever use of iterated sampling--importance resampling (ISIR) to form a bias-reduced version of the estimator. We furnish the proposed algorithm with rigorous theoretical results, including new bias, variance and high-probability bounds, and these are illustrated by numerical examples.

Ex$^2$MCMC: Sampling through Exploration Exploitation

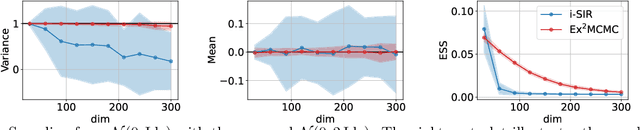
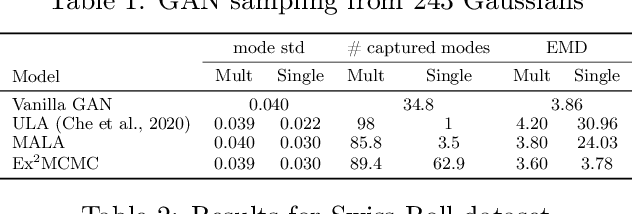
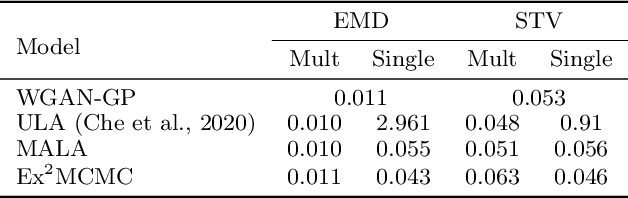
We develop an Explore-Exploit Markov chain Monte Carlo algorithm ($\operatorname{Ex^2MCMC}$) that combines multiple global proposals and local moves. The proposed method is massively parallelizable and extremely computationally efficient. We prove $V$-uniform geometric ergodicity of $\operatorname{Ex^2MCMC}$ under realistic conditions and compute explicit bounds on the mixing rate showing the improvement brought by the multiple global moves. We show that $\operatorname{Ex^2MCMC}$ allows fine-tuning of exploitation (local moves) and exploration (global moves) via a novel approach to proposing dependent global moves. Finally, we develop an adaptive scheme, $\operatorname{FlEx^2MCMC}$, that learns the distribution of global moves using normalizing flows. We illustrate the efficiency of $\operatorname{Ex^2MCMC}$ and its adaptive versions on many classical sampling benchmarks. We also show that these algorithms improve the quality of sampling GANs as energy-based models.

Monte Carlo Variational Auto-Encoders

Variational auto-encoders (VAE) are popular deep latent variable models which are trained by maximizing an Evidence Lower Bound (ELBO). To obtain tighter ELBO and hence better variational approximations, it has been proposed to use importance sampling to get a lower variance estimate of the evidence. However, importance sampling is known to perform poorly in high dimensions. While it has been suggested many times in the literature to use more sophisticated algorithms such as Annealed Importance Sampling (AIS) and its Sequential Importance Sampling (SIS) extensions, the potential benefits brought by these advanced techniques have never been realized for VAE: the AIS estimate cannot be easily differentiated, while SIS requires the specification of carefully chosen backward Markov kernels. In this paper, we address both issues and demonstrate the performance of the resulting Monte Carlo VAEs on a variety of applications.

Invertible Flow Non Equilibrium sampling

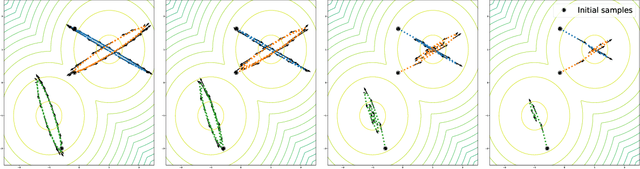
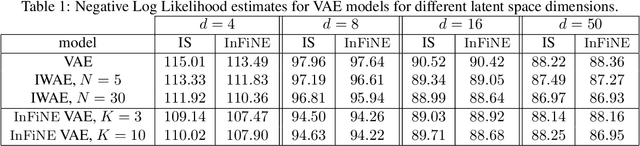
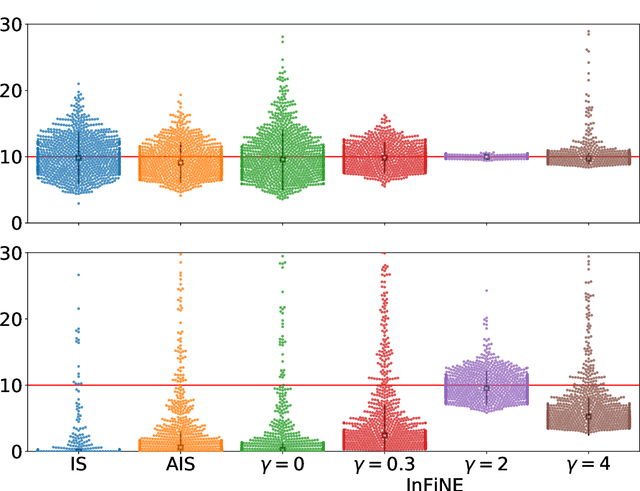
Simultaneously sampling from a complex distribution with intractable normalizing constant and approximating expectations under this distribution is a notoriously challenging problem. We introduce a novel scheme, Invertible Flow Non Equilibrium Sampling (InFine), which departs from classical Sequential Monte Carlo (SMC) and Markov chain Monte Carlo (MCMC) approaches. InFine constructs unbiased estimators of expectations and in particular of normalizing constants by combining the orbits of a deterministic transform started from random initializations.When this transform is chosen as an appropriate integrator of a conformal Hamiltonian system, these orbits are optimization paths. InFine is also naturally suited to design new MCMC sampling schemes by selecting samples on the optimization paths.Additionally, InFine can be used to construct an Evidence Lower Bound (ELBO) leading to a new class of Variational AutoEncoders (VAE).

Nonreversible MCMC from conditional invertible transforms: a complete recipe with convergence guarantees

Markov Chain Monte Carlo (MCMC) is a class of algorithms to sample complex and high-dimensional probability distributions. The Metropolis-Hastings (MH) algorithm, the workhorse of MCMC, provides a simple recipe to construct reversible Markov kernels. Reversibility is a tractable property which implies a less tractable but essential property here, invariance. Reversibility is however not necessarily desirable when considering performance. This has prompted recent interest in designing kernels breaking this property. At the same time, an active stream of research has focused on the design of novel versions of the MH kernel, some nonreversible, relying on the use of complex invertible deterministic transforms. While standard implementations of the MH kernel are well understood, aforementioned developments have not received the same systematic treatment to ensure their validity. This paper fills the gap by developing general tools to ensure that a class of nonreversible Markov kernels, possibly relying on complex transforms, has the desired invariance property and lead to convergent algorithms. This leads to a set of simple and practically verifiable conditions.

MetFlow: A New Efficient Method for Bridging the Gap between Markov Chain Monte Carlo and Variational Inference

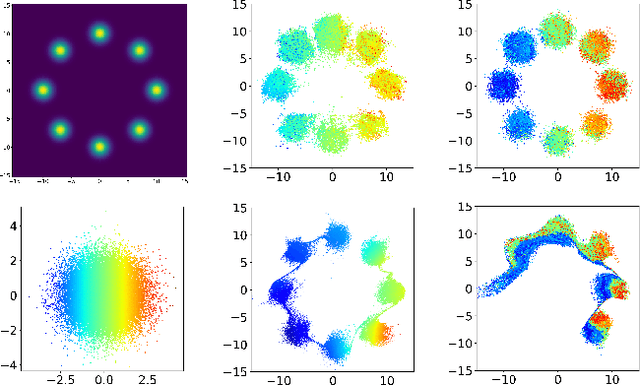
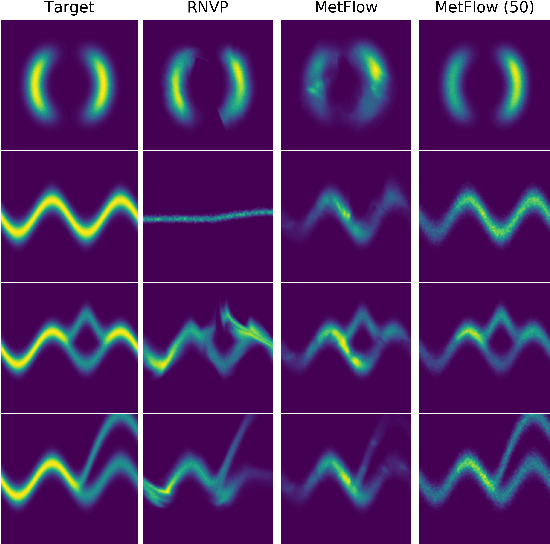
In this contribution, we propose a new computationally efficient method to combine Variational Inference (VI) with Markov Chain Monte Carlo (MCMC). This approach can be used with generic MCMC kernels, but is especially well suited to \textit{MetFlow}, a novel family of MCMC algorithms we introduce, in which proposals are obtained using Normalizing Flows. The marginal distribution produced by such MCMC algorithms is a mixture of flow-based distributions, thus drastically increasing the expressivity of the variational family. Unlike previous methods following this direction, our approach is amenable to the reparametrization trick and does not rely on computationally expensive reverse kernels. Extensive numerical experiments show clear computational and performance improvements over state-of-the-art methods.