Interpreting Neural Networks through the Polytope Lens

Mechanistic interpretability aims to explain what a neural network has learned at a nuts-and-bolts level. What are the fundamental primitives of neural network representations? Previous mechanistic descriptions have used individual neurons or their linear combinations to understand the representations a network has learned. But there are clues that neurons and their linear combinations are not the correct fundamental units of description: directions cannot describe how neural networks use nonlinearities to structure their representations. Moreover, many instances of individual neurons and their combinations are polysemantic (i.e. they have multiple unrelated meanings). Polysemanticity makes interpreting the network in terms of neurons or directions challenging since we can no longer assign a specific feature to a neural unit. In order to find a basic unit of description that does not suffer from these problems, we zoom in beyond just directions to study the way that piecewise linear activation functions (such as ReLU) partition the activation space into numerous discrete polytopes. We call this perspective the polytope lens. The polytope lens makes concrete predictions about the behavior of neural networks, which we evaluate through experiments on both convolutional image classifiers and language models. Specifically, we show that polytopes can be used to identify monosemantic regions of activation space (while directions are not in general monosemantic) and that the density of polytope boundaries reflect semantic boundaries. We also outline a vision for what mechanistic interpretability might look like through the polytope lens.

MetFlow: A New Efficient Method for Bridging the Gap between Markov Chain Monte Carlo and Variational Inference

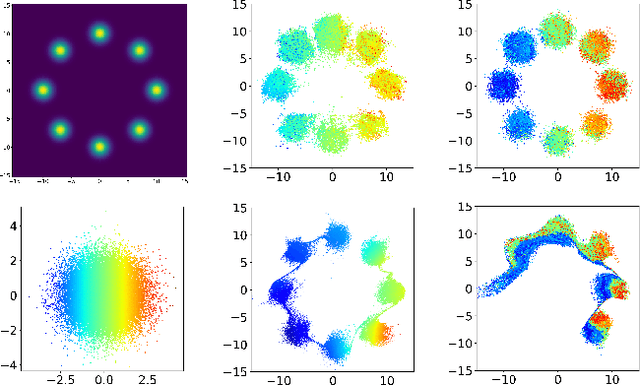
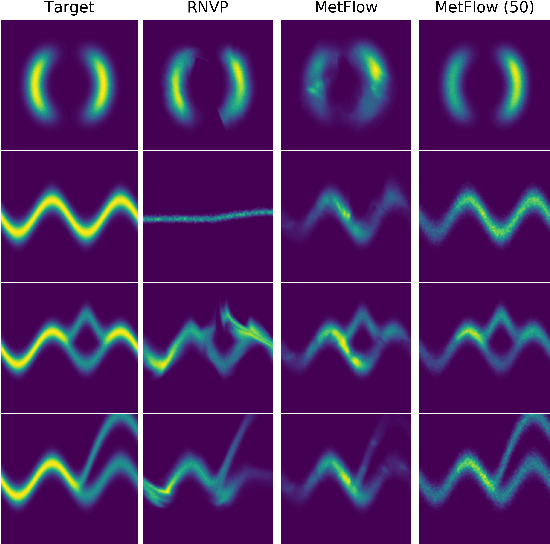
In this contribution, we propose a new computationally efficient method to combine Variational Inference (VI) with Markov Chain Monte Carlo (MCMC). This approach can be used with generic MCMC kernels, but is especially well suited to \textit{MetFlow}, a novel family of MCMC algorithms we introduce, in which proposals are obtained using Normalizing Flows. The marginal distribution produced by such MCMC algorithms is a mixture of flow-based distributions, thus drastically increasing the expressivity of the variational family. Unlike previous methods following this direction, our approach is amenable to the reparametrization trick and does not rely on computationally expensive reverse kernels. Extensive numerical experiments show clear computational and performance improvements over state-of-the-art methods.