FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI

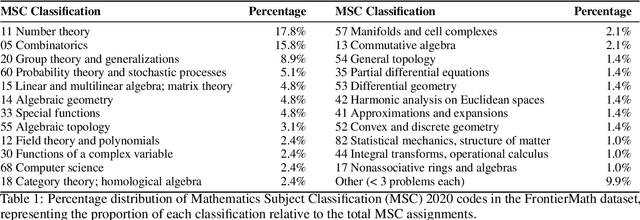
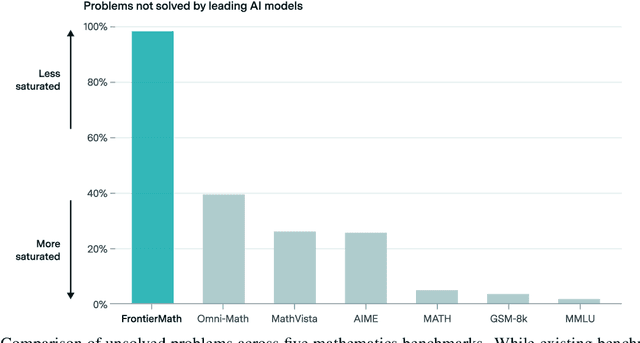
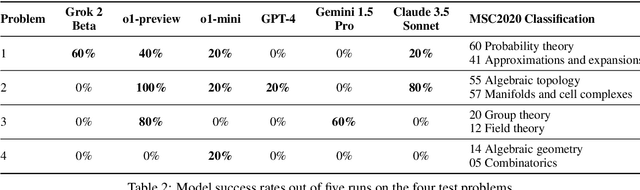
We introduce FrontierMath, a benchmark of hundreds of original, exceptionally challenging mathematics problems crafted and vetted by expert mathematicians. The questions cover most major branches of modern mathematics -- from computationally intensive problems in number theory and real analysis to abstract questions in algebraic geometry and category theory. Solving a typical problem requires multiple hours of effort from a researcher in the relevant branch of mathematics, and for the upper end questions, multiple days. FrontierMath uses new, unpublished problems and automated verification to reliably evaluate models while minimizing risk of data contamination. Current state-of-the-art AI models solve under 2% of problems, revealing a vast gap between AI capabilities and the prowess of the mathematical community. As AI systems advance toward expert-level mathematical abilities, FrontierMath offers a rigorous testbed that quantifies their progress.

AI capabilities can be significantly improved without expensive retraining

State-of-the-art AI systems can be significantly improved without expensive retraining via "post-training enhancements"-techniques applied after initial training like fine-tuning the system to use a web browser. We review recent post-training enhancements, categorizing them into five types: tool-use, prompting methods, scaffolding, solution selection, and data generation. Different enhancements improve performance on different tasks, making it hard to compare their significance. So we translate improvements from different enhancements into a common currency, the compute-equivalent gain: how much additional training compute would be needed to improve performance by the same amount as the enhancement. Our non-experimental work shows that post-training enhancements have significant benefits: most surveyed enhancements improve benchmark performance by more than a 5x increase in training compute, some by more than 20x. Post-training enhancements are relatively cheap to develop: fine-tuning costs are typically <1% of the original training cost. Governing the development of capable post-training enhancements may be challenging because frontier models could be enhanced by a wide range of actors.

Overthinking the Truth: Understanding how Language Models Process False Demonstrations

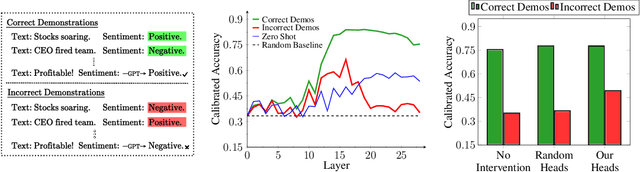
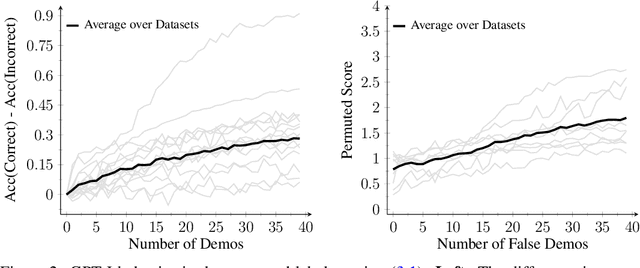
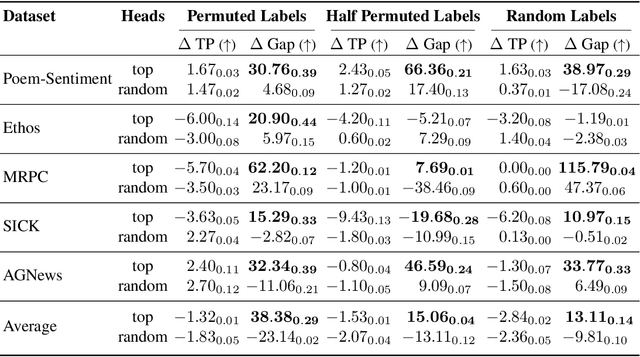
Modern language models can imitate complex patterns through few-shot learning, enabling them to complete challenging tasks without fine-tuning. However, imitation can also lead models to reproduce inaccuracies or harmful content if present in the context. We study harmful imitation through the lens of a model's internal representations, and identify two related phenomena: overthinking and false induction heads. The first phenomenon, overthinking, appears when we decode predictions from intermediate layers, given correct vs. incorrect few-shot demonstrations. At early layers, both demonstrations induce similar model behavior, but the behavior diverges sharply at some "critical layer", after which the accuracy given incorrect demonstrations progressively decreases. The second phenomenon, false induction heads, are a possible mechanistic cause of overthinking: these are heads in late layers that attend to and copy false information from previous demonstrations, and whose ablation reduces overthinking. Beyond scientific understanding, our results suggest that studying intermediate model computations could be a promising avenue for understanding and guarding against harmful model behaviors.

Auditing Visualizations: Transparency Methods Struggle to Detect Anomalous Behavior

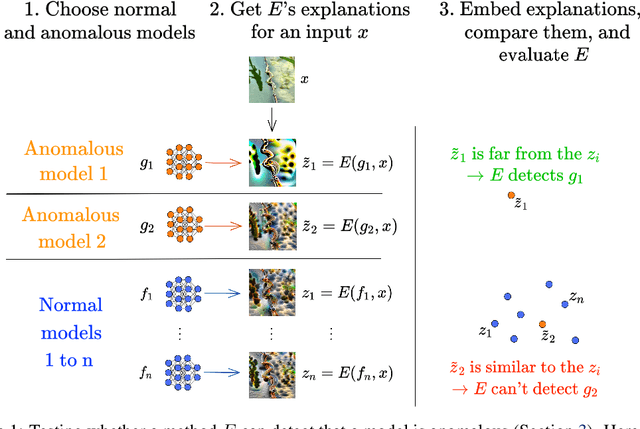
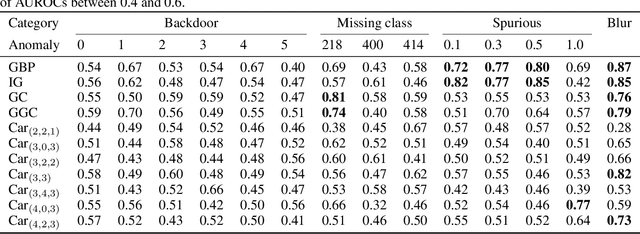
Transparency methods such as model visualizations provide information that outputs alone might miss, since they describe the internals of neural networks. But can we trust that model explanations reflect model behavior? For instance, can they diagnose abnormal behavior such as backdoors or shape bias? To evaluate model explanations, we define a model as anomalous if it differs from a reference set of normal models, and we test whether transparency methods assign different explanations to anomalous and normal models. We find that while existing methods can detect stark anomalies such as shape bias or adversarial training, they struggle to identify more subtle anomalies such as models trained on incomplete data. Moreover, they generally fail to distinguish the inputs that induce anomalous behavior, e.g. images containing a backdoor trigger. These results reveal new blind spots in existing model explanations, pointing to the need for further method development.

Grounding Representation Similarity with Statistical Testing

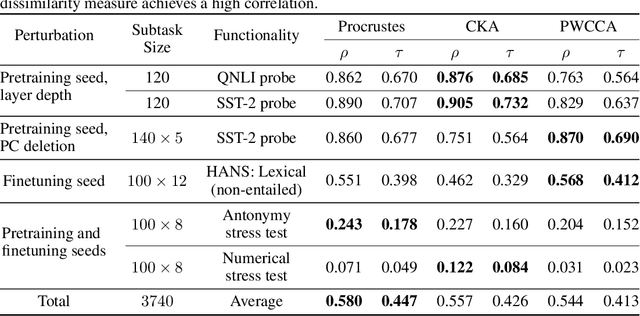
To understand neural network behavior, recent works quantitatively compare different networks' learned representations using canonical correlation analysis (CCA), centered kernel alignment (CKA), and other dissimilarity measures. Unfortunately, these widely used measures often disagree on fundamental observations, such as whether deep networks differing only in random initialization learn similar representations. These disagreements raise the question: which, if any, of these dissimilarity measures should we believe? We provide a framework to ground this question through a concrete test: measures should have sensitivity to changes that affect functional behavior, and specificity against changes that do not. We quantify this through a variety of functional behaviors including probing accuracy and robustness to distribution shift, and examine changes such as varying random initialization and deleting principal components. We find that current metrics exhibit different weaknesses, note that a classical baseline performs surprisingly well, and highlight settings where all metrics appear to fail, thus providing a challenge set for further improvement.

MetFlow: A New Efficient Method for Bridging the Gap between Markov Chain Monte Carlo and Variational Inference

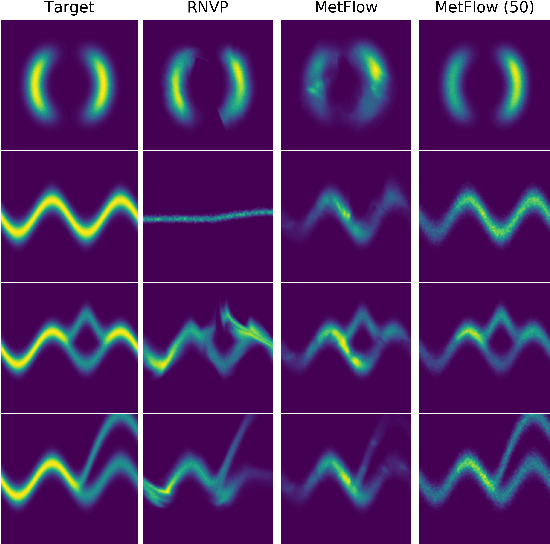
In this contribution, we propose a new computationally efficient method to combine Variational Inference (VI) with Markov Chain Monte Carlo (MCMC). This approach can be used with generic MCMC kernels, but is especially well suited to \textit{MetFlow}, a novel family of MCMC algorithms we introduce, in which proposals are obtained using Normalizing Flows. The marginal distribution produced by such MCMC algorithms is a mixture of flow-based distributions, thus drastically increasing the expressivity of the variational family. Unlike previous methods following this direction, our approach is amenable to the reparametrization trick and does not rely on computationally expensive reverse kernels. Extensive numerical experiments show clear computational and performance improvements over state-of-the-art methods.