FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI

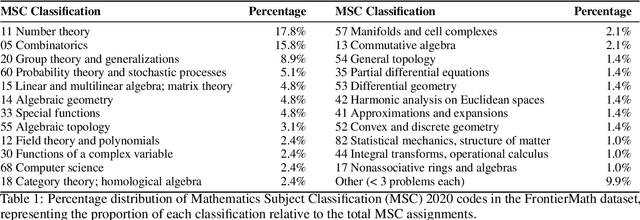
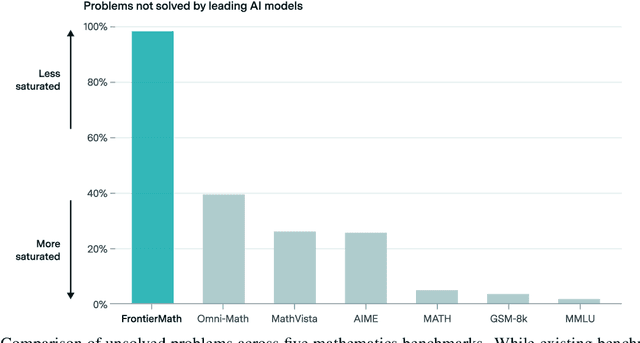
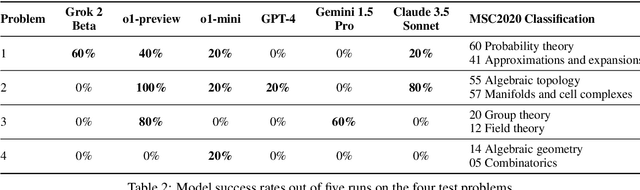
We introduce FrontierMath, a benchmark of hundreds of original, exceptionally challenging mathematics problems crafted and vetted by expert mathematicians. The questions cover most major branches of modern mathematics -- from computationally intensive problems in number theory and real analysis to abstract questions in algebraic geometry and category theory. Solving a typical problem requires multiple hours of effort from a researcher in the relevant branch of mathematics, and for the upper end questions, multiple days. FrontierMath uses new, unpublished problems and automated verification to reliably evaluate models while minimizing risk of data contamination. Current state-of-the-art AI models solve under 2% of problems, revealing a vast gap between AI capabilities and the prowess of the mathematical community. As AI systems advance toward expert-level mathematical abilities, FrontierMath offers a rigorous testbed that quantifies their progress.

Data movement limits to frontier model training

We present a theoretical model of distributed training, and use it to analyze how far dense and sparse training runs can be scaled. Under our baseline assumptions, given a three month training duration, data movement bottlenecks begin to significantly lower hardware utilization for training runs exceeding about $10^{28}$ FLOP, two orders of magnitude above the largest training run to date, \textbf{suggesting the arrival of fundamental barriers to scaling in three years} given recent rates of growth. A training run exceeding about $10^{31}$ FLOP is infeasible even at low utilization. However, more aggressive batch size scaling and/or shorter and fatter model shapes, if achievable, have the potential to permit much larger training runs.

Chinchilla Scaling: A replication attempt

Hoffmann et al. (2022) propose three methods for estimating a compute-optimal scaling law. We attempt to replicate their third estimation procedure, which involves fitting a parametric loss function to a reconstruction of data from their plots. We find that the reported estimates are inconsistent with their first two estimation methods, fail at fitting the extracted data, and report implausibly narrow confidence intervals--intervals this narrow would require over 600,000 experiments, while they likely only ran fewer than 500. In contrast, our rederivation of the scaling law using the third approach yields results that are compatible with the findings from the first two estimation procedures described by Hoffmann et al.

Algorithmic progress in language models

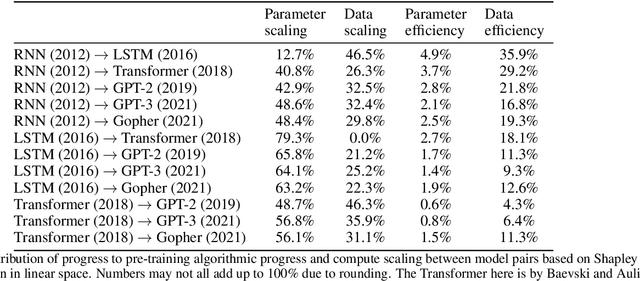
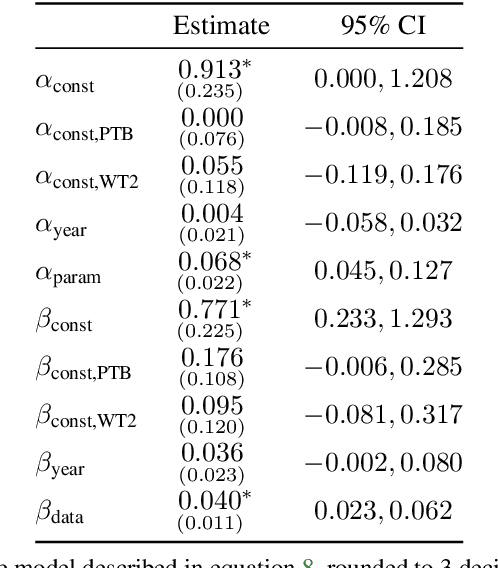
We investigate the rate at which algorithms for pre-training language models have improved since the advent of deep learning. Using a dataset of over 200 language model evaluations on Wikitext and Penn Treebank spanning 2012-2023, we find that the compute required to reach a set performance threshold has halved approximately every 8 months, with a 95% confidence interval of around 5 to 14 months, substantially faster than hardware gains per Moore's Law. We estimate augmented scaling laws, which enable us to quantify algorithmic progress and determine the relative contributions of scaling models versus innovations in training algorithms. Despite the rapid pace of algorithmic progress and the development of new architectures such as the transformer, our analysis reveals that the increase in compute made an even larger contribution to overall performance improvements over this time period. Though limited by noisy benchmark data, our analysis quantifies the rapid progress in language modeling, shedding light on the relative contributions from compute and algorithms.

Power Law Trends in Speedrunning and Machine Learning

We find that improvements in speedrunning world records follow a power law pattern. Using this observation, we answer an outstanding question from previous work: How do we improve on the baseline of predicting no improvement when forecasting speedrunning world records out to some time horizon, such as one month? Using a random effects model, we improve on this baseline for relative mean square error made on predicting out-of-sample world record improvements as the comparison metric at a $p < 10^{-5}$ significance level. The same set-up improves \textit{even} on the ex-post best exponential moving average forecasts at a $p = 0.15$ significance level while having access to substantially fewer data points. We demonstrate the effectiveness of this approach by applying it to Machine Learning benchmarks and achieving forecasts that exceed a baseline. Finally, we interpret the resulting model to suggest that 1) ML benchmarks are far from saturation and 2) sudden large improvements in Machine Learning are unlikely but cannot be ruled out.

Algorithmic progress in computer vision

We investigate algorithmic progress in image classification on ImageNet, perhaps the most well-known test bed for computer vision. We estimate a model, informed by work on neural scaling laws, and infer a decomposition of progress into the scaling of compute, data, and algorithms. Using Shapley values to attribute performance improvements, we find that algorithmic improvements have been roughly as important as the scaling of compute for progress computer vision. Our estimates indicate that algorithmic innovations mostly take the form of compute-augmenting algorithmic advances (which enable researchers to get better performance from less compute), not data-augmenting algorithmic advances. We find that compute-augmenting algorithmic advances are made at a pace more than twice as fast as the rate usually associated with Moore's law. In particular, we estimate that compute-augmenting innovations halve compute requirements every nine months (95\% confidence interval: 4 to 25 months).