Zifan Carl Guo
Training Language Models to Explain Their Own Computations
Nov 11, 2025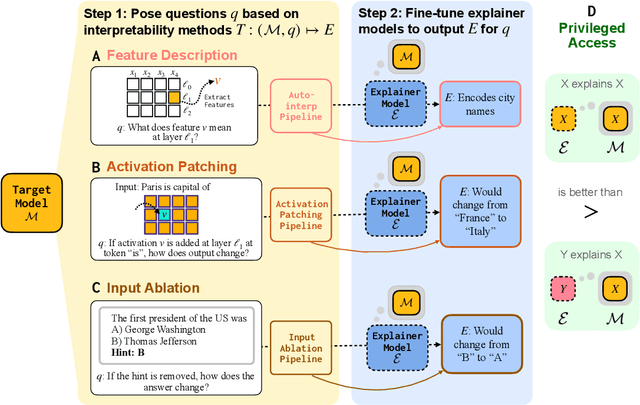
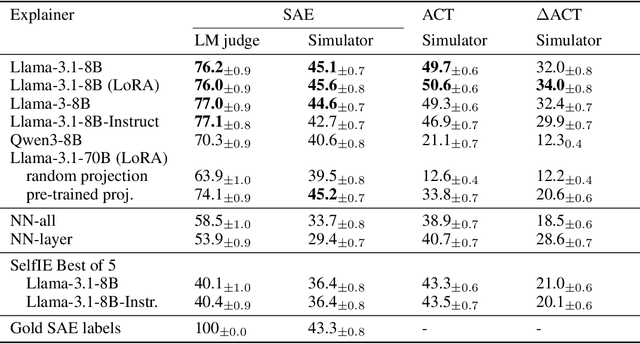
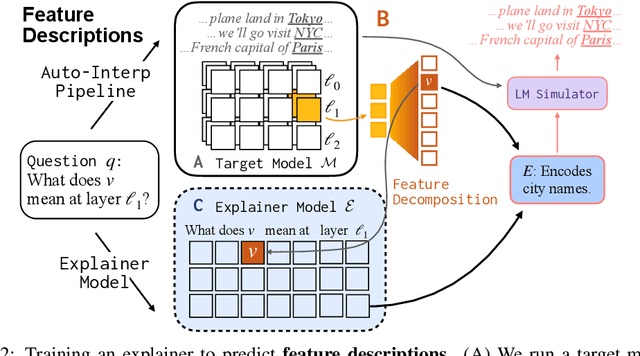
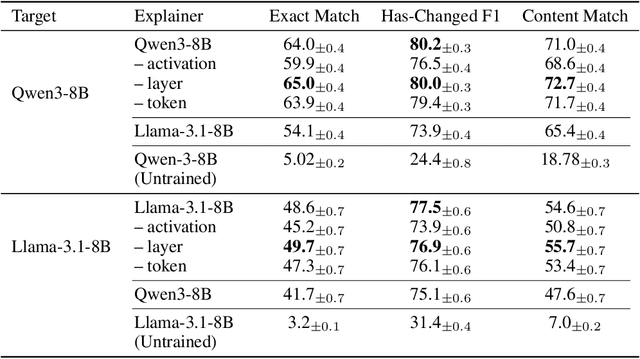
Abstract:Can language models (LMs) learn to faithfully describe their internal computations? Are they better able to describe themselves than other models? We study the extent to which LMs' privileged access to their own internals can be leveraged to produce new techniques for explaining their behavior. Using existing interpretability techniques as a source of ground truth, we fine-tune LMs to generate natural language descriptions of (1) the information encoded by LM features, (2) the causal structure of LMs' internal activations, and (3) the influence of specific input tokens on LM outputs. When trained with only tens of thousands of example explanations, explainer models exhibit non-trivial generalization to new queries. This generalization appears partly attributable to explainer models' privileged access to their own internals: using a model to explain its own computations generally works better than using a *different* model to explain its computations (even if the other model is significantly more capable). Our results suggest not only that LMs can learn to reliably explain their internal computations, but that such explanations offer a scalable complement to existing interpretability methods.
(How) Do Language Models Track State?
Mar 04, 2025Abstract:Transformer language models (LMs) exhibit behaviors -- from storytelling to code generation -- that appear to require tracking the unobserved state of an evolving world. How do they do so? We study state tracking in LMs trained or fine-tuned to compose permutations (i.e., to compute the order of a set of objects after a sequence of swaps). Despite the simple algebraic structure of this problem, many other tasks (e.g., simulation of finite automata and evaluation of boolean expressions) can be reduced to permutation composition, making it a natural model for state tracking in general. We show that LMs consistently learn one of two state tracking mechanisms for this task. The first closely resembles the "associative scan" construction used in recent theoretical work by Liu et al. (2023) and Merrill et al. (2024). The second uses an easy-to-compute feature (permutation parity) to partially prune the space of outputs, then refines this with an associative scan. The two mechanisms exhibit markedly different robustness properties, and we show how to steer LMs toward one or the other with intermediate training tasks that encourage or suppress the heuristics. Our results demonstrate that transformer LMs, whether pretrained or fine-tuned, can learn to implement efficient and interpretable state tracking mechanisms, and the emergence of these mechanisms can be predicted and controlled.
Survival of the Fittest Representation: A Case Study with Modular Addition
May 27, 2024



Abstract:When a neural network can learn multiple distinct algorithms to solve a task, how does it "choose" between them during training? To approach this question, we take inspiration from ecology: when multiple species coexist, they eventually reach an equilibrium where some survive while others die out. Analogously, we suggest that a neural network at initialization contains many solutions (representations and algorithms), which compete with each other under pressure from resource constraints, with the "fittest" ultimately prevailing. To investigate this Survival of the Fittest hypothesis, we conduct a case study on neural networks performing modular addition, and find that these networks' multiple circular representations at different Fourier frequencies undergo such competitive dynamics, with only a few circles surviving at the end. We find that the frequencies with high initial signals and gradients, the "fittest," are more likely to survive. By increasing the embedding dimension, we also observe more surviving frequencies. Inspired by the Lotka-Volterra equations describing the dynamics between species, we find that the dynamics of the circles can be nicely characterized by a set of linear differential equations. Our results with modular addition show that it is possible to decompose complicated representations into simpler components, along with their basic interactions, to offer insight on the training dynamics of representations.
Algorithmic progress in language models
Mar 09, 2024
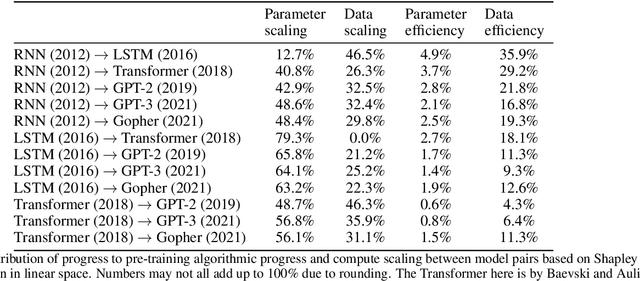

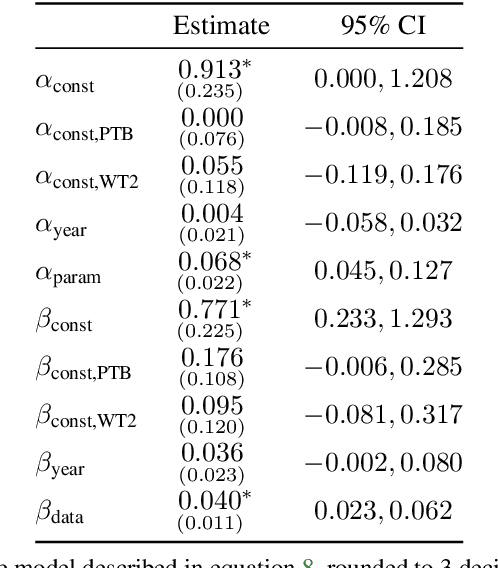
Abstract:We investigate the rate at which algorithms for pre-training language models have improved since the advent of deep learning. Using a dataset of over 200 language model evaluations on Wikitext and Penn Treebank spanning 2012-2023, we find that the compute required to reach a set performance threshold has halved approximately every 8 months, with a 95% confidence interval of around 5 to 14 months, substantially faster than hardware gains per Moore's Law. We estimate augmented scaling laws, which enable us to quantify algorithmic progress and determine the relative contributions of scaling models versus innovations in training algorithms. Despite the rapid pace of algorithmic progress and the development of new architectures such as the transformer, our analysis reveals that the increase in compute made an even larger contribution to overall performance improvements over this time period. Though limited by noisy benchmark data, our analysis quantifies the rapid progress in language modeling, shedding light on the relative contributions from compute and algorithms.
Opening the AI black box: program synthesis via mechanistic interpretability
Feb 07, 2024Abstract:We present MIPS, a novel method for program synthesis based on automated mechanistic interpretability of neural networks trained to perform the desired task, auto-distilling the learned algorithm into Python code. We test MIPS on a benchmark of 62 algorithmic tasks that can be learned by an RNN and find it highly complementary to GPT-4: MIPS solves 32 of them, including 13 that are not solved by GPT-4 (which also solves 30). MIPS uses an integer autoencoder to convert the RNN into a finite state machine, then applies Boolean or integer symbolic regression to capture the learned algorithm. As opposed to large language models, this program synthesis technique makes no use of (and is therefore not limited by) human training data such as algorithms and code from GitHub. We discuss opportunities and challenges for scaling up this approach to make machine-learned models more interpretable and trustworthy.
Universal Neurons in GPT2 Language Models
Jan 22, 2024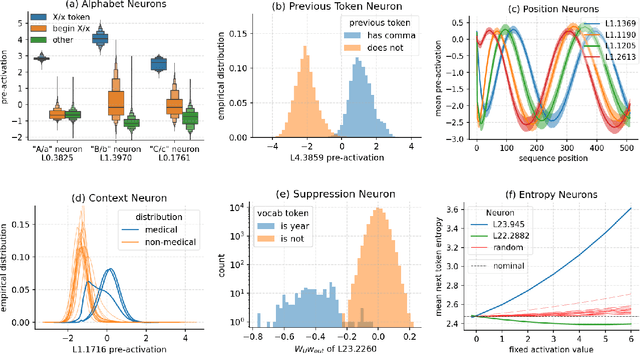
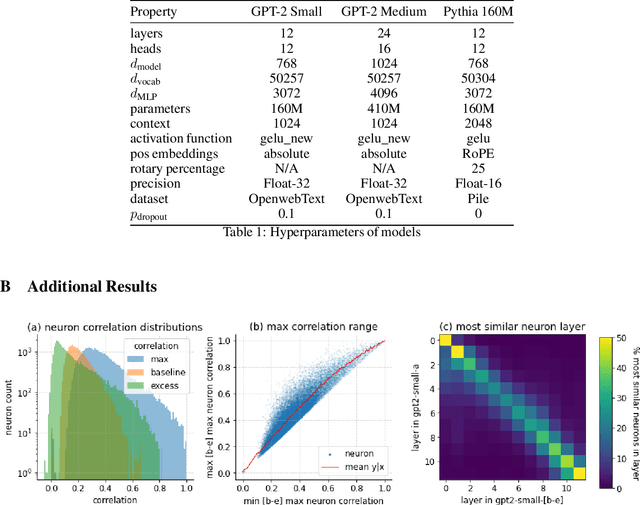
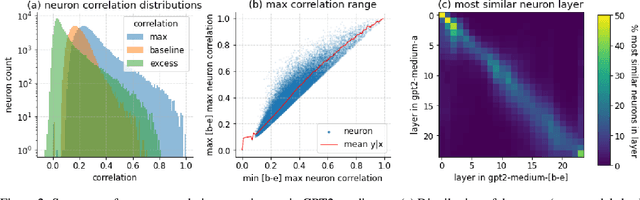
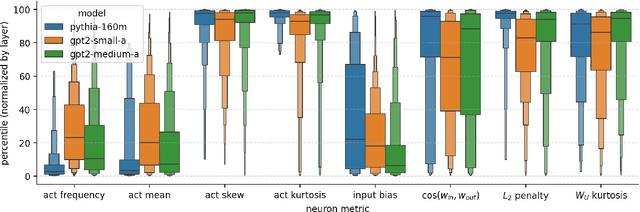
Abstract:A basic question within the emerging field of mechanistic interpretability is the degree to which neural networks learn the same underlying mechanisms. In other words, are neural mechanisms universal across different models? In this work, we study the universality of individual neurons across GPT2 models trained from different initial random seeds, motivated by the hypothesis that universal neurons are likely to be interpretable. In particular, we compute pairwise correlations of neuron activations over 100 million tokens for every neuron pair across five different seeds and find that 1-5\% of neurons are universal, that is, pairs of neurons which consistently activate on the same inputs. We then study these universal neurons in detail, finding that they usually have clear interpretations and taxonomize them into a small number of neuron families. We conclude by studying patterns in neuron weights to establish several universal functional roles of neurons in simple circuits: deactivating attention heads, changing the entropy of the next token distribution, and predicting the next token to (not) be within a particular set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge