The Singapore Consensus on Global AI Safety Research Priorities

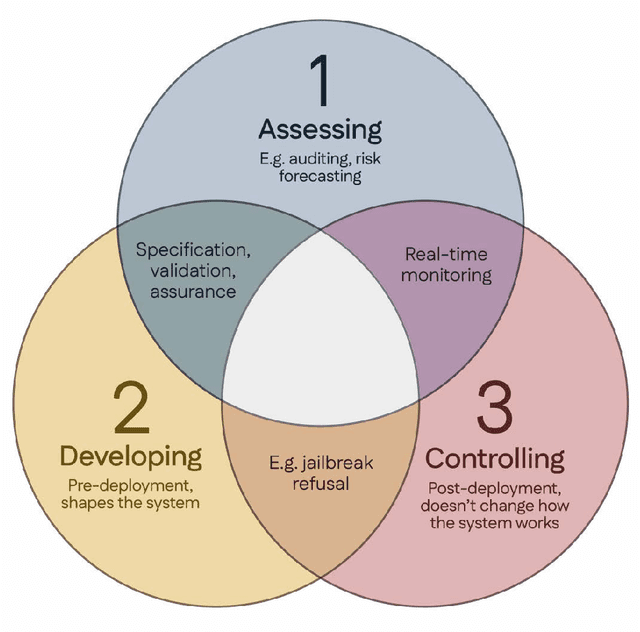
Rapidly improving AI capabilities and autonomy hold significant promise of transformation, but are also driving vigorous debate on how to ensure that AI is safe, i.e., trustworthy, reliable, and secure. Building a trusted ecosystem is therefore essential -- it helps people embrace AI with confidence and gives maximal space for innovation while avoiding backlash. The "2025 Singapore Conference on AI (SCAI): International Scientific Exchange on AI Safety" aimed to support research in this space by bringing together AI scientists across geographies to identify and synthesise research priorities in AI safety. This resulting report builds on the International AI Safety Report chaired by Yoshua Bengio and backed by 33 governments. By adopting a defence-in-depth model, this report organises AI safety research domains into three types: challenges with creating trustworthy AI systems (Development), challenges with evaluating their risks (Assessment), and challenges with monitoring and intervening after deployment (Control).

Dense SAE Latents Are Features, Not Bugs

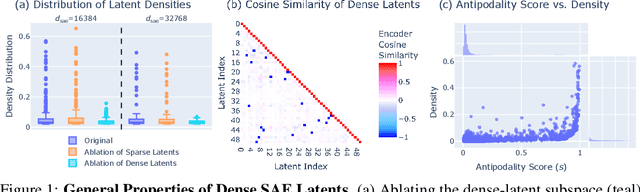
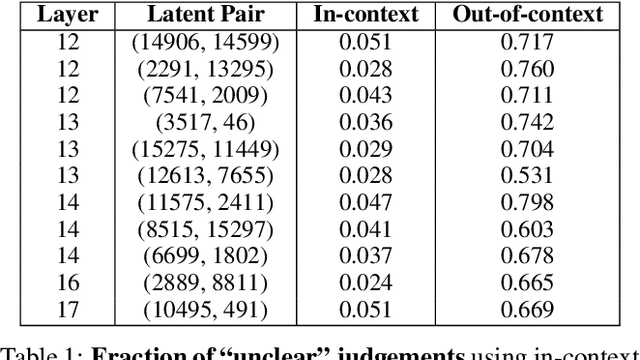
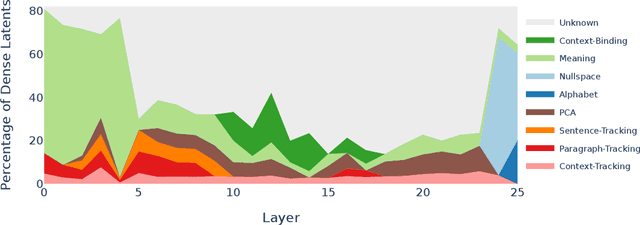
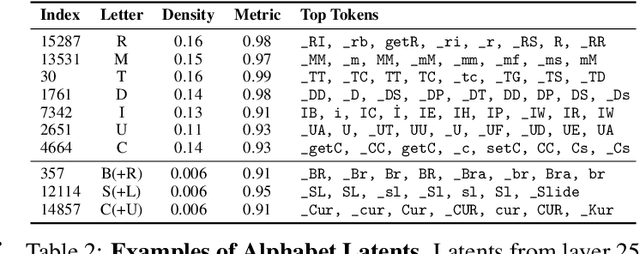
Sparse autoencoders (SAEs) are designed to extract interpretable features from language models by enforcing a sparsity constraint. Ideally, training an SAE would yield latents that are both sparse and semantically meaningful. However, many SAE latents activate frequently (i.e., are \emph{dense}), raising concerns that they may be undesirable artifacts of the training procedure. In this work, we systematically investigate the geometry, function, and origin of dense latents and show that they are not only persistent but often reflect meaningful model representations. We first demonstrate that dense latents tend to form antipodal pairs that reconstruct specific directions in the residual stream, and that ablating their subspace suppresses the emergence of new dense features in retrained SAEs -- suggesting that high density features are an intrinsic property of the residual space. We then introduce a taxonomy of dense latents, identifying classes tied to position tracking, context binding, entropy regulation, letter-specific output signals, part-of-speech, and principal component reconstruction. Finally, we analyze how these features evolve across layers, revealing a shift from structural features in early layers, to semantic features in mid layers, and finally to output-oriented signals in the last layers of the model. Our findings indicate that dense latents serve functional roles in language model computation and should not be dismissed as training noise.

On the creation of narrow AI: hierarchy and nonlocality of neural network skills

We study the problem of creating strong, yet narrow, AI systems. While recent AI progress has been driven by the training of large general-purpose foundation models, the creation of smaller models specialized for narrow domains could be valuable for both efficiency and safety. In this work, we explore two challenges involved in creating such systems, having to do with basic properties of how neural networks learn and structure their representations. The first challenge regards when it is possible to train narrow models from scratch. Through experiments on a synthetic task, we find that it is sometimes necessary to train networks on a wide distribution of data to learn certain narrow skills within that distribution. This effect arises when skills depend on each other hierarchically, and training on a broad distribution introduces a curriculum which substantially accelerates learning. The second challenge regards how to transfer particular skills from large general models into small specialized models. We find that model skills are often not perfectly localized to a particular set of prunable components. However, we find that methods based on pruning can still outperform distillation. We investigate the use of a regularization objective to align desired skills with prunable components while unlearning unnecessary skills.

Neural Thermodynamic Laws for Large Language Model Training

Beyond neural scaling laws, little is known about the laws underlying large language models (LLMs). We introduce Neural Thermodynamic Laws (NTL) -- a new framework that offers fresh insights into LLM training dynamics. On the theoretical side, we demonstrate that key thermodynamic quantities (e.g., temperature, entropy, heat capacity, thermal conduction) and classical thermodynamic principles (e.g., the three laws of thermodynamics and the equipartition theorem) naturally emerge under river-valley loss landscape assumptions. On the practical side, this scientific perspective yields intuitive guidelines for designing learning rate schedules.

Scaling Laws For Scalable Oversight

Scalable oversight, the process by which weaker AI systems supervise stronger ones, has been proposed as a key strategy to control future superintelligent systems. However, it is still unclear how scalable oversight itself scales. To address this gap, we propose a framework that quantifies the probability of successful oversight as a function of the capabilities of the overseer and the system being overseen. Specifically, our framework models oversight as a game between capability-mismatched players; the players have oversight-specific and deception-specific Elo scores that are a piecewise-linear function of their general intelligence, with two plateaus corresponding to task incompetence and task saturation. We validate our framework with a modified version of the game Nim and then apply it to four oversight games: "Mafia", "Debate", "Backdoor Code" and "Wargames". For each game, we find scaling laws that approximate how domain performance depends on general AI system capability (using Chatbot Arena Elo as a proxy for general capability). We then build on our findings in a theoretical study of Nested Scalable Oversight (NSO), a process in which trusted models oversee untrusted stronger models, which then become the trusted models in the next step. We identify conditions under which NSO succeeds and derive numerically (and in some cases analytically) the optimal number of oversight levels to maximize the probability of oversight success. In our numerical examples, the NSO success rate is below 52% when overseeing systems that are 400 Elo points stronger than the baseline overseer, and it declines further for overseeing even stronger systems.

Do Two AI Scientists Agree?

When two AI models are trained on the same scientific task, do they learn the same theory or two different theories? Throughout history of science, we have witnessed the rise and fall of theories driven by experimental validation or falsification: many theories may co-exist when experimental data is lacking, but the space of survived theories become more constrained with more experimental data becoming available. We show the same story is true for AI scientists. With increasingly more systems provided in training data, AI scientists tend to converge in the theories they learned, although sometimes they form distinct groups corresponding to different theories. To mechanistically interpret what theories AI scientists learn and quantify their agreement, we propose MASS, Hamiltonian-Lagrangian neural networks as AI Scientists, trained on standard problems in physics, aggregating training results across many seeds simulating the different configurations of AI scientists. Our findings suggests for AI scientists switch from learning a Hamiltonian theory in simple setups to a Lagrangian formulation when more complex systems are introduced. We also observe strong seed dependence of the training dynamics and final learned weights, controlling the rise and fall of relevant theories. We finally demonstrate that not only can our neural networks aid interpretability, it can also be applied to higher dimensional problems.

Towards Understanding Distilled Reasoning Models: A Representational Approach

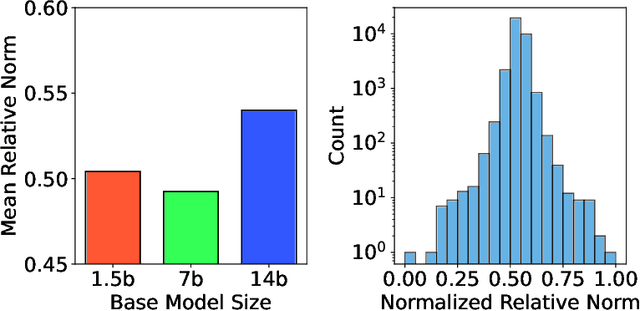
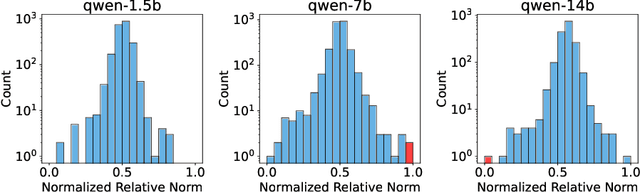
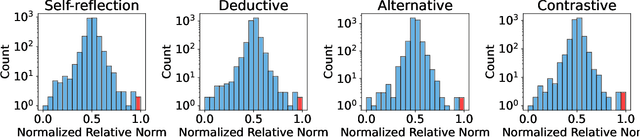
In this paper, we investigate how model distillation impacts the development of reasoning features in large language models (LLMs). To explore this, we train a crosscoder on Qwen-series models and their fine-tuned variants. Our results suggest that the crosscoder learns features corresponding to various types of reasoning, including self-reflection and computation verification. Moreover, we observe that distilled models contain unique reasoning feature directions, which could be used to steer the model into over-thinking or incisive-thinking mode. In particular, we perform analysis on four specific reasoning categories: (a) self-reflection, (b) deductive reasoning, (c) alternative reasoning, and (d) contrastive reasoning. Finally, we examine the changes in feature geometry resulting from the distillation process and find indications that larger distilled models may develop more structured representations, which correlate with enhanced distillation performance. By providing insights into how distillation modifies the model, our study contributes to enhancing the transparency and reliability of AI systems.

Are Sparse Autoencoders Useful? A Case Study in Sparse Probing

Sparse autoencoders (SAEs) are a popular method for interpreting concepts represented in large language model (LLM) activations. However, there is a lack of evidence regarding the validity of their interpretations due to the lack of a ground truth for the concepts used by an LLM, and a growing number of works have presented problems with current SAEs. One alternative source of evidence would be demonstrating that SAEs improve performance on downstream tasks beyond existing baselines. We test this by applying SAEs to the real-world task of LLM activation probing in four regimes: data scarcity, class imbalance, label noise, and covariate shift. Due to the difficulty of detecting concepts in these challenging settings, we hypothesize that SAEs' basis of interpretable, concept-level latents should provide a useful inductive bias. However, although SAEs occasionally perform better than baselines on individual datasets, we are unable to design ensemble methods combining SAEs with baselines that consistently outperform ensemble methods solely using baselines. Additionally, although SAEs initially appear promising for identifying spurious correlations, detecting poor dataset quality, and training multi-token probes, we are able to achieve similar results with simple non-SAE baselines as well. Though we cannot discount SAEs' utility on other tasks, our findings highlight the shortcomings of current SAEs and the need to rigorously evaluate interpretability methods on downstream tasks with strong baselines.

Harmonic Loss Trains Interpretable AI Models

In this paper, we introduce **harmonic loss** as an alternative to the standard cross-entropy loss for training neural networks and large language models (LLMs). Harmonic loss enables improved interpretability and faster convergence, owing to its scale invariance and finite convergence point by design, which can be interpreted as a class center. We first validate the performance of harmonic models across algorithmic, vision, and language datasets. Through extensive experiments, we demonstrate that models trained with harmonic loss outperform standard models by: (a) enhancing interpretability, (b) requiring less data for generalization, and (c) reducing grokking. Moreover, we compare a GPT-2 model trained with harmonic loss to the standard GPT-2, illustrating that the harmonic model develops more interpretable representations. Looking forward, we believe harmonic loss has the potential to become a valuable tool in domains with limited data availability or in high-stakes applications where interpretability and reliability are paramount, paving the way for more robust and efficient neural network models.

Language Models Use Trigonometry to Do Addition

Mathematical reasoning is an increasingly important indicator of large language model (LLM) capabilities, yet we lack understanding of how LLMs process even simple mathematical tasks. To address this, we reverse engineer how three mid-sized LLMs compute addition. We first discover that numbers are represented in these LLMs as a generalized helix, which is strongly causally implicated for the tasks of addition and subtraction, and is also causally relevant for integer division, multiplication, and modular arithmetic. We then propose that LLMs compute addition by manipulating this generalized helix using the "Clock" algorithm: to solve $a+b$, the helices for $a$ and $b$ are manipulated to produce the $a+b$ answer helix which is then read out to model logits. We model influential MLP outputs, attention head outputs, and even individual neuron preactivations with these helices and verify our understanding with causal interventions. By demonstrating that LLMs represent numbers on a helix and manipulate this helix to perform addition, we present the first representation-level explanation of an LLM's mathematical capability.