On the creation of narrow AI: hierarchy and nonlocality of neural network skills

We study the problem of creating strong, yet narrow, AI systems. While recent AI progress has been driven by the training of large general-purpose foundation models, the creation of smaller models specialized for narrow domains could be valuable for both efficiency and safety. In this work, we explore two challenges involved in creating such systems, having to do with basic properties of how neural networks learn and structure their representations. The first challenge regards when it is possible to train narrow models from scratch. Through experiments on a synthetic task, we find that it is sometimes necessary to train networks on a wide distribution of data to learn certain narrow skills within that distribution. This effect arises when skills depend on each other hierarchically, and training on a broad distribution introduces a curriculum which substantially accelerates learning. The second challenge regards how to transfer particular skills from large general models into small specialized models. We find that model skills are often not perfectly localized to a particular set of prunable components. However, we find that methods based on pruning can still outperform distillation. We investigate the use of a regularization objective to align desired skills with prunable components while unlearning unnecessary skills.

Open Problems in Mechanistic Interpretability

Mechanistic interpretability aims to understand the computational mechanisms underlying neural networks' capabilities in order to accomplish concrete scientific and engineering goals. Progress in this field thus promises to provide greater assurance over AI system behavior and shed light on exciting scientific questions about the nature of intelligence. Despite recent progress toward these goals, there are many open problems in the field that require solutions before many scientific and practical benefits can be realized: Our methods require both conceptual and practical improvements to reveal deeper insights; we must figure out how best to apply our methods in pursuit of specific goals; and the field must grapple with socio-technical challenges that influence and are influenced by our work. This forward-facing review discusses the current frontier of mechanistic interpretability and the open problems that the field may benefit from prioritizing.

Physics of Skill Learning

We aim to understand physics of skill learning, i.e., how skills are learned in neural networks during training. We start by observing the Domino effect, i.e., skills are learned sequentially, and notably, some skills kick off learning right after others complete learning, similar to the sequential fall of domino cards. To understand the Domino effect and relevant behaviors of skill learning, we take physicists' approach of abstraction and simplification. We propose three models with varying complexities -- the Geometry model, the Resource model, and the Domino model, trading between reality and simplicity. The Domino effect can be reproduced in the Geometry model, whose resource interpretation inspires the Resource model, which can be further simplified to the Domino model. These models present different levels of abstraction and simplification; each is useful to study some aspects of skill learning. The Geometry model provides interesting insights into neural scaling laws and optimizers; the Resource model sheds light on the learning dynamics of compositional tasks; the Domino model reveals the benefits of modularity. These models are not only conceptually interesting -- e.g., we show how Chinchilla scaling laws can emerge from the Geometry model, but also are useful in practice by inspiring algorithmic development -- e.g., we show how simple algorithmic changes, motivated by these toy models, can speed up the training of deep learning models.

Efficient Dictionary Learning with Switch Sparse Autoencoders

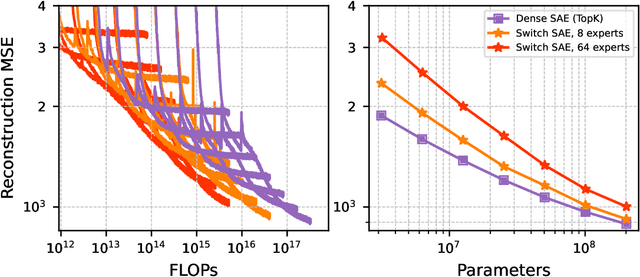
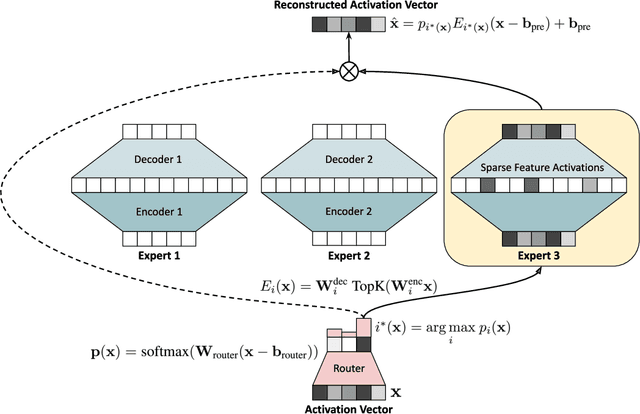
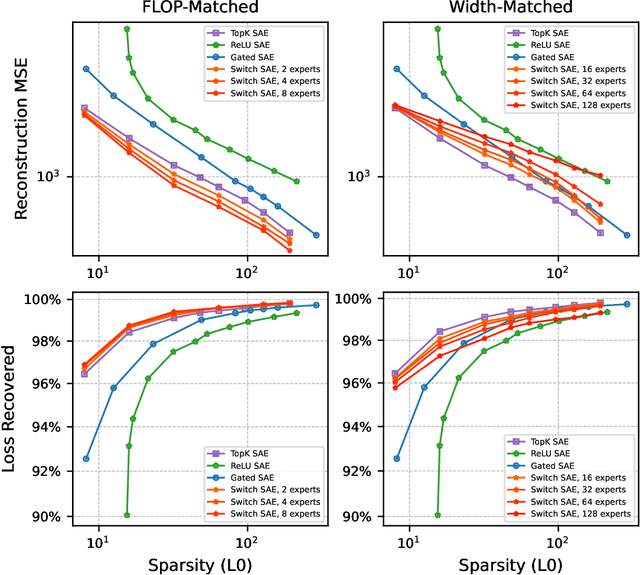
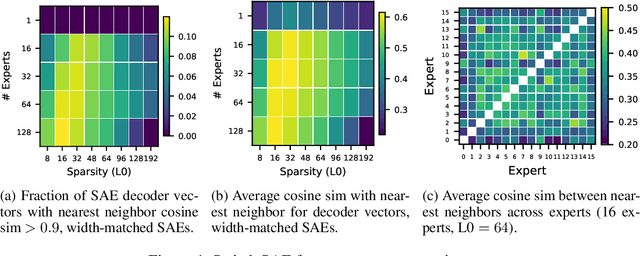
Sparse autoencoders (SAEs) are a recent technique for decomposing neural network activations into human-interpretable features. However, in order for SAEs to identify all features represented in frontier models, it will be necessary to scale them up to very high width, posing a computational challenge. In this work, we introduce Switch Sparse Autoencoders, a novel SAE architecture aimed at reducing the compute cost of training SAEs. Inspired by sparse mixture of experts models, Switch SAEs route activation vectors between smaller "expert" SAEs, enabling SAEs to efficiently scale to many more features. We present experiments comparing Switch SAEs with other SAE architectures, and find that Switch SAEs deliver a substantial Pareto improvement in the reconstruction vs. sparsity frontier for a given fixed training compute budget. We also study the geometry of features across experts, analyze features duplicated across experts, and verify that Switch SAE features are as interpretable as features found by other SAE architectures.

Survival of the Fittest Representation: A Case Study with Modular Addition

When a neural network can learn multiple distinct algorithms to solve a task, how does it "choose" between them during training? To approach this question, we take inspiration from ecology: when multiple species coexist, they eventually reach an equilibrium where some survive while others die out. Analogously, we suggest that a neural network at initialization contains many solutions (representations and algorithms), which compete with each other under pressure from resource constraints, with the "fittest" ultimately prevailing. To investigate this Survival of the Fittest hypothesis, we conduct a case study on neural networks performing modular addition, and find that these networks' multiple circular representations at different Fourier frequencies undergo such competitive dynamics, with only a few circles surviving at the end. We find that the frequencies with high initial signals and gradients, the "fittest," are more likely to survive. By increasing the embedding dimension, we also observe more surviving frequencies. Inspired by the Lotka-Volterra equations describing the dynamics between species, we find that the dynamics of the circles can be nicely characterized by a set of linear differential equations. Our results with modular addition show that it is possible to decompose complicated representations into simpler components, along with their basic interactions, to offer insight on the training dynamics of representations.

Not All Language Model Features Are Linear

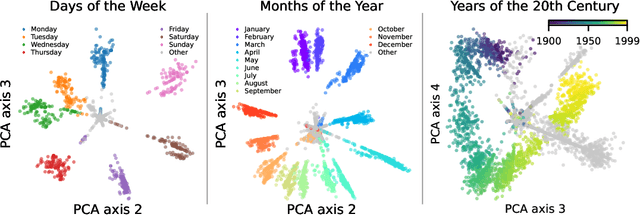
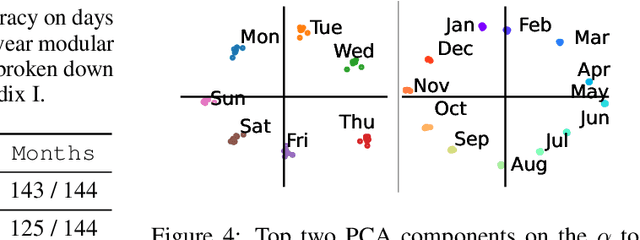
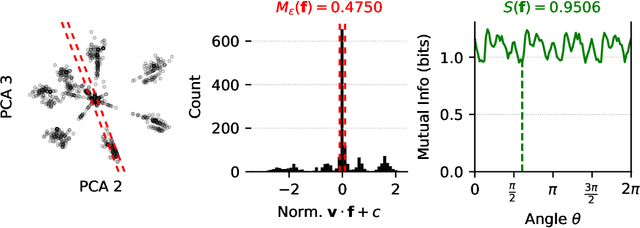
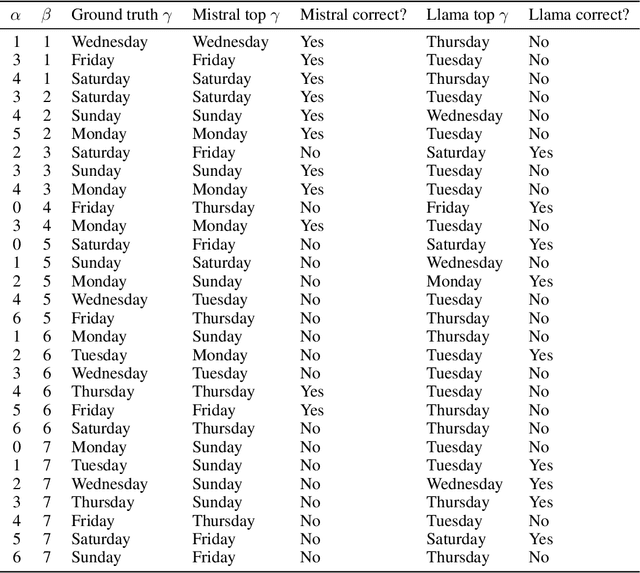
Recent work has proposed the linear representation hypothesis: that language models perform computation by manipulating one-dimensional representations of concepts ("features") in activation space. In contrast, we explore whether some language model representations may be inherently multi-dimensional. We begin by developing a rigorous definition of irreducible multi-dimensional features based on whether they can be decomposed into either independent or non-co-occurring lower-dimensional features. Motivated by these definitions, we design a scalable method that uses sparse autoencoders to automatically find multi-dimensional features in GPT-2 and Mistral 7B. These auto-discovered features include strikingly interpretable examples, e.g. circular features representing days of the week and months of the year. We identify tasks where these exact circles are used to solve computational problems involving modular arithmetic in days of the week and months of the year. Finally, we provide evidence that these circular features are indeed the fundamental unit of computation in these tasks with intervention experiments on Mistral 7B and Llama 3 8B, and we find further circular representations by breaking down the hidden states for these tasks into interpretable components.

Sparse Feature Circuits: Discovering and Editing Interpretable Causal Graphs in Language Models

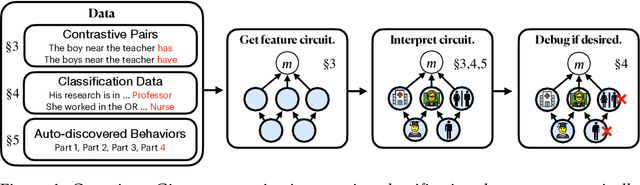
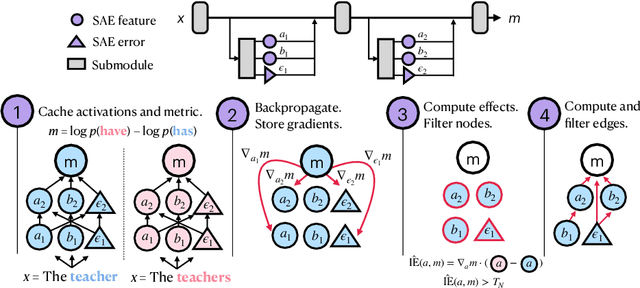
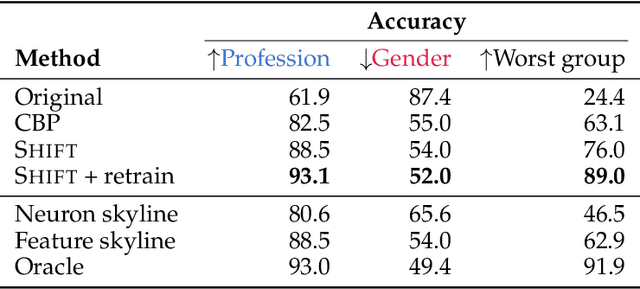
We introduce methods for discovering and applying sparse feature circuits. These are causally implicated subnetworks of human-interpretable features for explaining language model behaviors. Circuits identified in prior work consist of polysemantic and difficult-to-interpret units like attention heads or neurons, rendering them unsuitable for many downstream applications. In contrast, sparse feature circuits enable detailed understanding of unanticipated mechanisms. Because they are based on fine-grained units, sparse feature circuits are useful for downstream tasks: We introduce SHIFT, where we improve the generalization of a classifier by ablating features that a human judges to be task-irrelevant. Finally, we demonstrate an entirely unsupervised and scalable interpretability pipeline by discovering thousands of sparse feature circuits for automatically discovered model behaviors.

Opening the AI black box: program synthesis via mechanistic interpretability

We present MIPS, a novel method for program synthesis based on automated mechanistic interpretability of neural networks trained to perform the desired task, auto-distilling the learned algorithm into Python code. We test MIPS on a benchmark of 62 algorithmic tasks that can be learned by an RNN and find it highly complementary to GPT-4: MIPS solves 32 of them, including 13 that are not solved by GPT-4 (which also solves 30). MIPS uses an integer autoencoder to convert the RNN into a finite state machine, then applies Boolean or integer symbolic regression to capture the learned algorithm. As opposed to large language models, this program synthesis technique makes no use of (and is therefore not limited by) human training data such as algorithms and code from GitHub. We discuss opportunities and challenges for scaling up this approach to make machine-learned models more interpretable and trustworthy.

Open Problems and Fundamental Limitations of Reinforcement Learning from Human Feedback

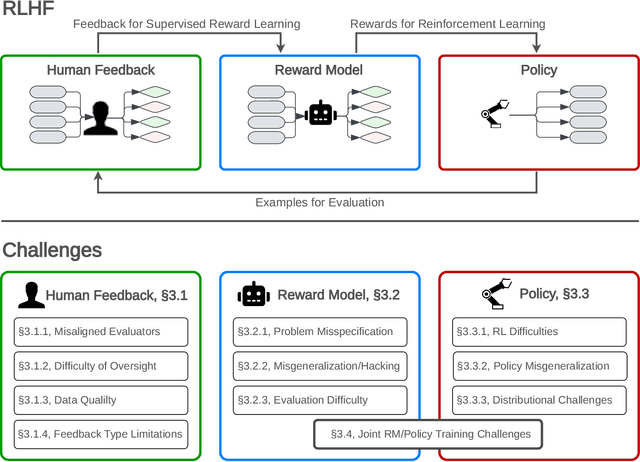
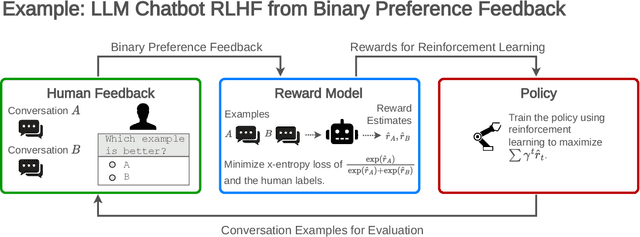
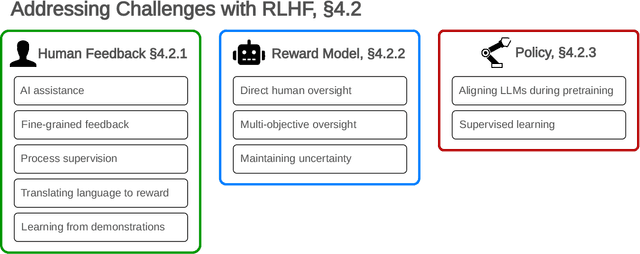
Reinforcement learning from human feedback (RLHF) is a technique for training AI systems to align with human goals. RLHF has emerged as the central method used to finetune state-of-the-art large language models (LLMs). Despite this popularity, there has been relatively little public work systematizing its flaws. In this paper, we (1) survey open problems and fundamental limitations of RLHF and related methods; (2) overview techniques to understand, improve, and complement RLHF in practice; and (3) propose auditing and disclosure standards to improve societal oversight of RLHF systems. Our work emphasizes the limitations of RLHF and highlights the importance of a multi-faceted approach to the development of safer AI systems.

The Quantization Model of Neural Scaling

We propose the $\textit{Quantization Model}$ of neural scaling laws, explaining both the observed power law dropoff of loss with model and data size, and also the sudden emergence of new capabilities with scale. We derive this model from what we call the $\textit{Quantization Hypothesis}$, where learned network capabilities are quantized into discrete chunks ($\textit{quanta}$). We show that when quanta are learned in order of decreasing use frequency, then a power law in use frequencies explains observed power law scaling of loss. We validate this prediction on toy datasets, then study how scaling curves decompose for large language models. Using language model internals, we auto-discover diverse model capabilities (quanta) and find tentative evidence that the distribution over corresponding subproblems in the prediction of natural text is compatible with the power law predicted from the neural scaling exponent as predicted from our theory.