Stochastic Parameter Decomposition

A key step in reverse engineering neural networks is to decompose them into simpler parts that can be studied in relative isolation. Linear parameter decomposition -- a framework that has been proposed to resolve several issues with current decomposition methods -- decomposes neural network parameters into a sum of sparsely used vectors in parameter space. However, the current main method in this framework, Attribution-based Parameter Decomposition (APD), is impractical on account of its computational cost and sensitivity to hyperparameters. In this work, we introduce \textit{Stochastic Parameter Decomposition} (SPD), a method that is more scalable and robust to hyperparameters than APD, which we demonstrate by decomposing models that are slightly larger and more complex than was possible to decompose with APD. We also show that SPD avoids other issues, such as shrinkage of the learned parameters, and better identifies ground truth mechanisms in toy models. By bridging causal mediation analysis and network decomposition methods, this demonstration opens up new research possibilities in mechanistic interpretability by removing barriers to scaling linear parameter decomposition methods to larger models. We release a library for running SPD and reproducing our experiments at https://github.com/goodfire-ai/spd.

Identifying Sparsely Active Circuits Through Local Loss Landscape Decomposition

Much of mechanistic interpretability has focused on understanding the activation spaces of large neural networks. However, activation space-based approaches reveal little about the underlying circuitry used to compute features. To better understand the circuits employed by models, we introduce a new decomposition method called Local Loss Landscape Decomposition (L3D). L3D identifies a set of low-rank subnetworks: directions in parameter space of which a subset can reconstruct the gradient of the loss between any sample's output and a reference output vector. We design a series of progressively more challenging toy models with well-defined subnetworks and show that L3D can nearly perfectly recover the associated subnetworks. Additionally, we investigate the extent to which perturbing the model in the direction of a given subnetwork affects only the relevant subset of samples. Finally, we apply L3D to a real-world transformer model and a convolutional neural network, demonstrating its potential to identify interpretable and relevant circuits in parameter space.

Open Problems in Mechanistic Interpretability

Mechanistic interpretability aims to understand the computational mechanisms underlying neural networks' capabilities in order to accomplish concrete scientific and engineering goals. Progress in this field thus promises to provide greater assurance over AI system behavior and shed light on exciting scientific questions about the nature of intelligence. Despite recent progress toward these goals, there are many open problems in the field that require solutions before many scientific and practical benefits can be realized: Our methods require both conceptual and practical improvements to reveal deeper insights; we must figure out how best to apply our methods in pursuit of specific goals; and the field must grapple with socio-technical challenges that influence and are influenced by our work. This forward-facing review discusses the current frontier of mechanistic interpretability and the open problems that the field may benefit from prioritizing.

Interpretability in Parameter Space: Minimizing Mechanistic Description Length with Attribution-based Parameter Decomposition

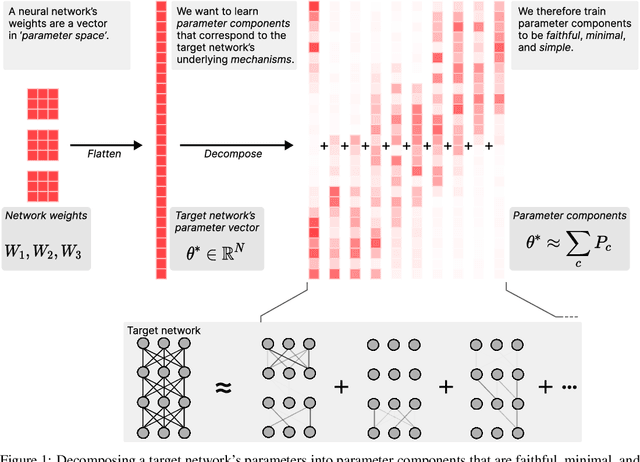
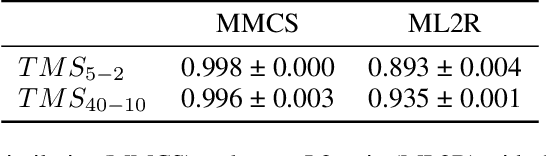
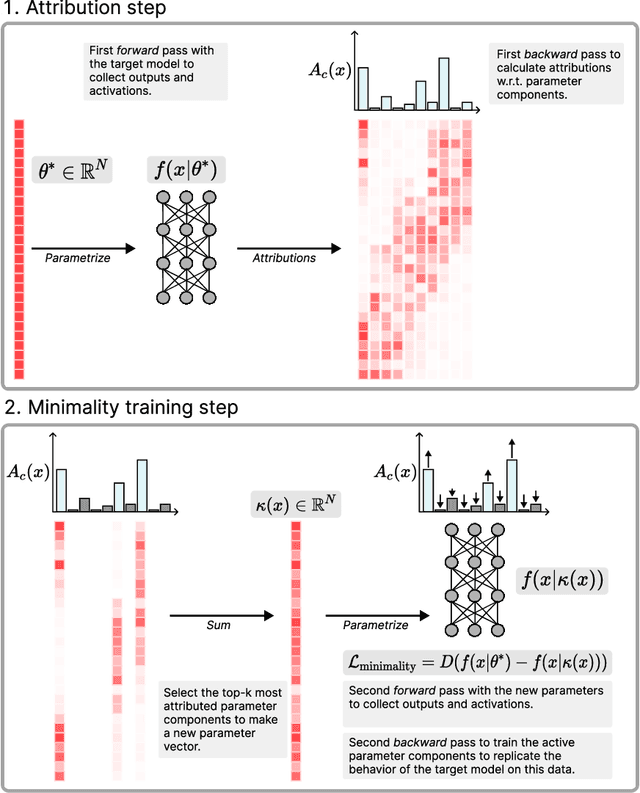
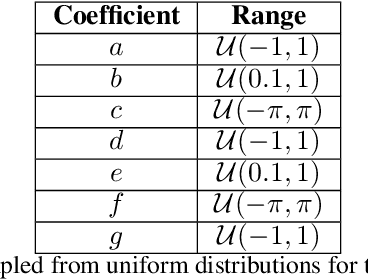
Mechanistic interpretability aims to understand the internal mechanisms learned by neural networks. Despite recent progress toward this goal, it remains unclear how best to decompose neural network parameters into mechanistic components. We introduce Attribution-based Parameter Decomposition (APD), a method that directly decomposes a neural network's parameters into components that (i) are faithful to the parameters of the original network, (ii) require a minimal number of components to process any input, and (iii) are maximally simple. Our approach thus optimizes for a minimal length description of the network's mechanisms. We demonstrate APD's effectiveness by successfully identifying ground truth mechanisms in multiple toy experimental settings: Recovering features from superposition; separating compressed computations; and identifying cross-layer distributed representations. While challenges remain to scaling APD to non-toy models, our results suggest solutions to several open problems in mechanistic interpretability, including identifying minimal circuits in superposition, offering a conceptual foundation for 'features', and providing an architecture-agnostic framework for neural network decomposition.

Towards evaluations-based safety cases for AI scheming

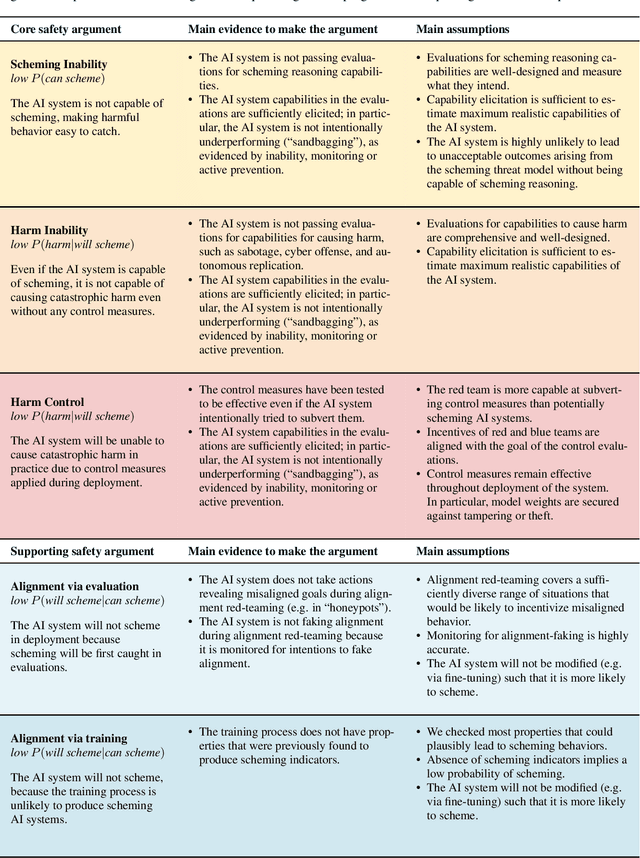
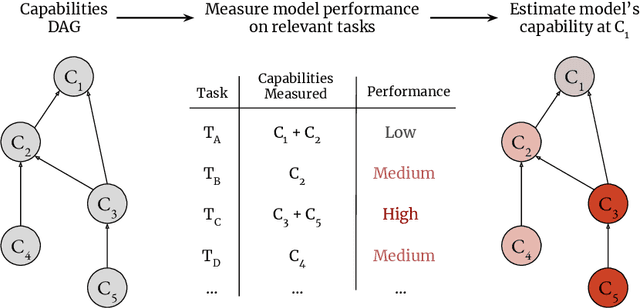
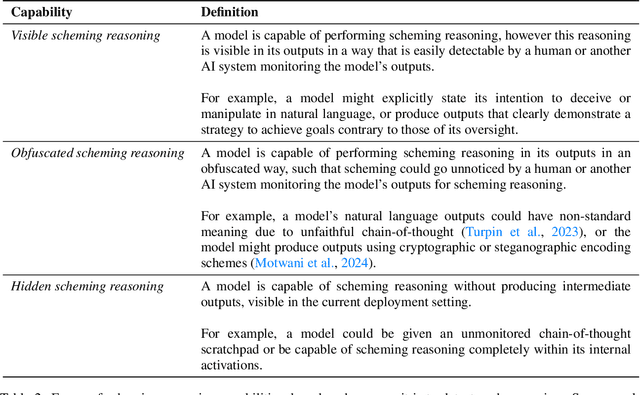
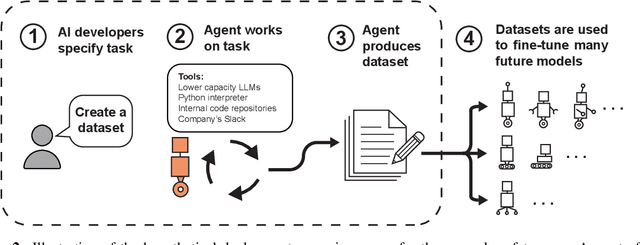
We sketch how developers of frontier AI systems could construct a structured rationale -- a 'safety case' -- that an AI system is unlikely to cause catastrophic outcomes through scheming. Scheming is a potential threat model where AI systems could pursue misaligned goals covertly, hiding their true capabilities and objectives. In this report, we propose three arguments that safety cases could use in relation to scheming. For each argument we sketch how evidence could be gathered from empirical evaluations, and what assumptions would need to be met to provide strong assurance. First, developers of frontier AI systems could argue that AI systems are not capable of scheming (Scheming Inability). Second, one could argue that AI systems are not capable of posing harm through scheming (Harm Inability). Third, one could argue that control measures around the AI systems would prevent unacceptable outcomes even if the AI systems intentionally attempted to subvert them (Harm Control). Additionally, we discuss how safety cases might be supported by evidence that an AI system is reasonably aligned with its developers (Alignment). Finally, we point out that many of the assumptions required to make these safety arguments have not been confidently satisfied to date and require making progress on multiple open research problems.

Using Degeneracy in the Loss Landscape for Mechanistic Interpretability

Mechanistic Interpretability aims to reverse engineer the algorithms implemented by neural networks by studying their weights and activations. An obstacle to reverse engineering neural networks is that many of the parameters inside a network are not involved in the computation being implemented by the network. These degenerate parameters may obfuscate internal structure. Singular learning theory teaches us that neural network parameterizations are biased towards being more degenerate, and parameterizations with more degeneracy are likely to generalize further. We identify 3 ways that network parameters can be degenerate: linear dependence between activations in a layer; linear dependence between gradients passed back to a layer; ReLUs which fire on the same subset of datapoints. We also present a heuristic argument that modular networks are likely to be more degenerate, and we develop a metric for identifying modules in a network that is based on this argument. We propose that if we can represent a neural network in a way that is invariant to reparameterizations that exploit the degeneracies, then this representation is likely to be more interpretable, and we provide some evidence that such a representation is likely to have sparser interactions. We introduce the Interaction Basis, a tractable technique to obtain a representation that is invariant to degeneracies from linear dependence of activations or Jacobians.

The Local Interaction Basis: Identifying Computationally-Relevant and Sparsely Interacting Features in Neural Networks

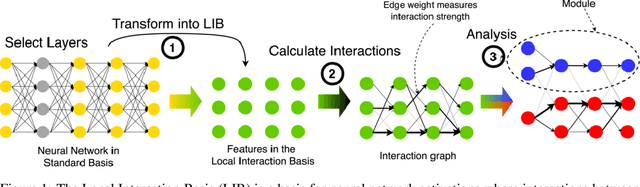
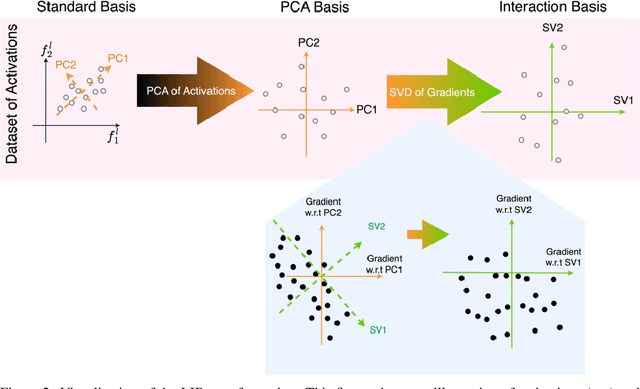
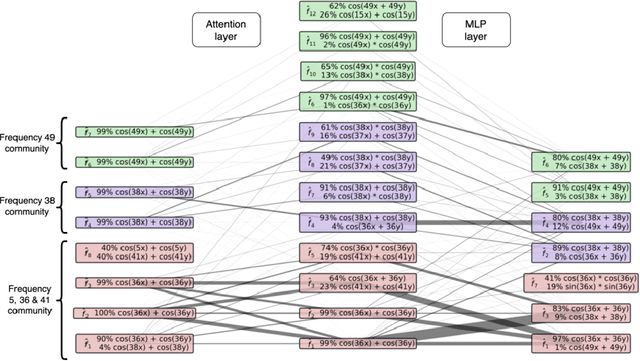
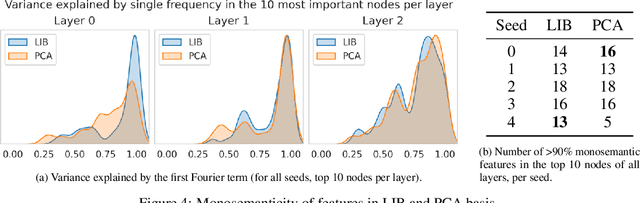
Mechanistic interpretability aims to understand the behavior of neural networks by reverse-engineering their internal computations. However, current methods struggle to find clear interpretations of neural network activations because a decomposition of activations into computational features is missing. Individual neurons or model components do not cleanly correspond to distinct features or functions. We present a novel interpretability method that aims to overcome this limitation by transforming the activations of the network into a new basis - the Local Interaction Basis (LIB). LIB aims to identify computational features by removing irrelevant activations and interactions. Our method drops irrelevant activation directions and aligns the basis with the singular vectors of the Jacobian matrix between adjacent layers. It also scales features based on their importance for downstream computation, producing an interaction graph that shows all computationally-relevant features and interactions in a model. We evaluate the effectiveness of LIB on modular addition and CIFAR-10 models, finding that it identifies more computationally-relevant features that interact more sparsely, compared to principal component analysis. However, LIB does not yield substantial improvements in interpretability or interaction sparsity when applied to language models. We conclude that LIB is a promising theory-driven approach for analyzing neural networks, but in its current form is not applicable to large language models.