Mathematical Models of Computation in Superposition

Superposition -- when a neural network represents more ``features'' than it has dimensions -- seems to pose a serious challenge to mechanistically interpreting current AI systems. Existing theory work studies \emph{representational} superposition, where superposition is only used when passing information through bottlenecks. In this work, we present mathematical models of \emph{computation} in superposition, where superposition is actively helpful for efficiently accomplishing the task. We first construct a task of efficiently emulating a circuit that takes the AND of the $\binom{m}{2}$ pairs of each of $m$ features. We construct a 1-layer MLP that uses superposition to perform this task up to $\varepsilon$-error, where the network only requires $\tilde{O}(m^{\frac{2}{3}})$ neurons, even when the input features are \emph{themselves in superposition}. We generalize this construction to arbitrary sparse boolean circuits of low depth, and then construct ``error correction'' layers that allow deep fully-connected networks of width $d$ to emulate circuits of width $\tilde{O}(d^{1.5})$ and \emph{any} polynomial depth. We conclude by providing some potential applications of our work for interpreting neural networks that implement computation in superposition.

Cluster-norm for Unsupervised Probing of Knowledge

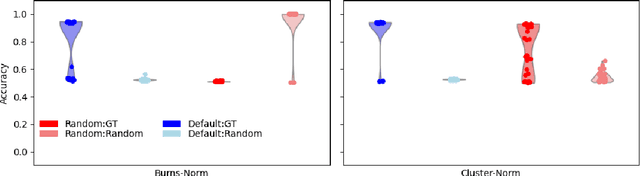
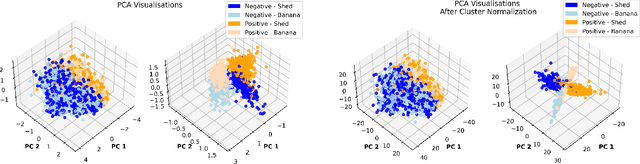
The deployment of language models brings challenges in generating reliable information, especially when these models are fine-tuned using human preferences. To extract encoded knowledge without (potentially) biased human labels, unsupervised probing techniques like Contrast-Consistent Search (CCS) have been developed (Burns et al., 2022). However, salient but unrelated features in a given dataset can mislead these probes (Farquhar et al., 2023). Addressing this, we propose a cluster normalization method to minimize the impact of such features by clustering and normalizing activations of contrast pairs before applying unsupervised probing techniques. While this approach does not address the issue of differentiating between knowledge in general and simulated knowledge - a major issue in the literature of latent knowledge elicitation (Christiano et al., 2021) - it significantly improves the ability of unsupervised probes to identify the intended knowledge amidst distractions.

The Local Interaction Basis: Identifying Computationally-Relevant and Sparsely Interacting Features in Neural Networks

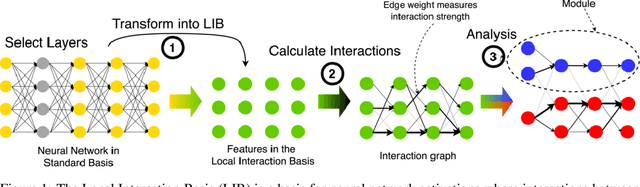
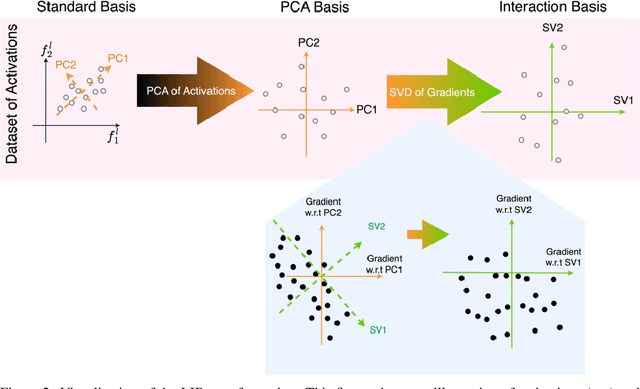
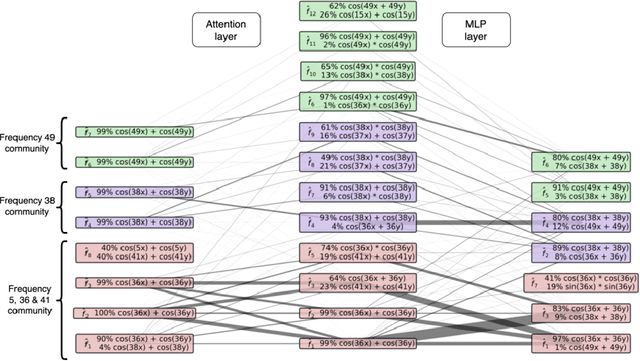
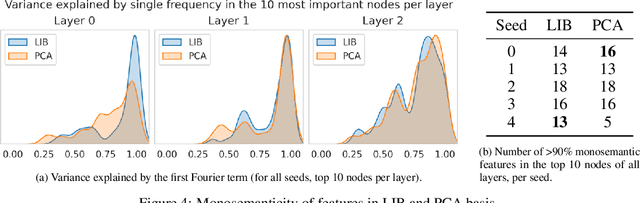
Mechanistic interpretability aims to understand the behavior of neural networks by reverse-engineering their internal computations. However, current methods struggle to find clear interpretations of neural network activations because a decomposition of activations into computational features is missing. Individual neurons or model components do not cleanly correspond to distinct features or functions. We present a novel interpretability method that aims to overcome this limitation by transforming the activations of the network into a new basis - the Local Interaction Basis (LIB). LIB aims to identify computational features by removing irrelevant activations and interactions. Our method drops irrelevant activation directions and aligns the basis with the singular vectors of the Jacobian matrix between adjacent layers. It also scales features based on their importance for downstream computation, producing an interaction graph that shows all computationally-relevant features and interactions in a model. We evaluate the effectiveness of LIB on modular addition and CIFAR-10 models, finding that it identifies more computationally-relevant features that interact more sparsely, compared to principal component analysis. However, LIB does not yield substantial improvements in interpretability or interaction sparsity when applied to language models. We conclude that LIB is a promising theory-driven approach for analyzing neural networks, but in its current form is not applicable to large language models.

Using Degeneracy in the Loss Landscape for Mechanistic Interpretability

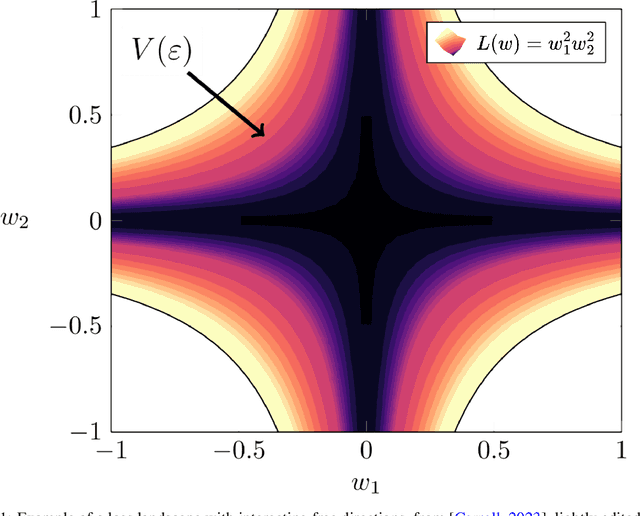
Mechanistic Interpretability aims to reverse engineer the algorithms implemented by neural networks by studying their weights and activations. An obstacle to reverse engineering neural networks is that many of the parameters inside a network are not involved in the computation being implemented by the network. These degenerate parameters may obfuscate internal structure. Singular learning theory teaches us that neural network parameterizations are biased towards being more degenerate, and parameterizations with more degeneracy are likely to generalize further. We identify 3 ways that network parameters can be degenerate: linear dependence between activations in a layer; linear dependence between gradients passed back to a layer; ReLUs which fire on the same subset of datapoints. We also present a heuristic argument that modular networks are likely to be more degenerate, and we develop a metric for identifying modules in a network that is based on this argument. We propose that if we can represent a neural network in a way that is invariant to reparameterizations that exploit the degeneracies, then this representation is likely to be more interpretable, and we provide some evidence that such a representation is likely to have sparser interactions. We introduce the Interaction Basis, a tractable technique to obtain a representation that is invariant to degeneracies from linear dependence of activations or Jacobians.