Inverse Depth Scaling From Most Layers Being Similar

Neural scaling laws relate loss to model size in large language models (LLMs), yet depth and width may contribute to performance differently, requiring more detailed studies. Here, we quantify how depth affects loss via analysis of LLMs and toy residual networks. We find loss scales inversely proportional to depth in LLMs, probably due to functionally similar layers reducing error through ensemble averaging rather than compositional learning or discretizing smooth dynamics. This regime is inefficient yet robust and may arise from the architectural bias of residual networks and target functions incompatible with smooth dynamics. The findings suggest that improving LLM efficiency may require architectural innovations to encourage compositional use of depth.

Universal One-third Time Scaling in Learning Peaked Distributions

Training large language models (LLMs) is computationally expensive, partly because the loss exhibits slow power-law convergence whose origin remains debatable. Through systematic analysis of toy models and empirical evaluation of LLMs, we show that this behavior can arise intrinsically from the use of softmax and cross-entropy. When learning peaked probability distributions, e.g., next-token distributions, these components yield power-law vanishing losses and gradients, creating a fundamental optimization bottleneck. This ultimately leads to power-law time scaling of the loss with a universal exponent of $1/3$. Our results provide a mechanistic explanation for observed neural scaling and suggest new directions for improving LLM training efficiency.

Superposition unifies power-law training dynamics

We investigate the role of feature superposition in the emergence of power-law training dynamics using a teacher-student framework. We first derive an analytic theory for training without superposition, establishing that the power-law training exponent depends on both the input data statistics and channel importance. Remarkably, we discover that a superposition bottleneck induces a transition to a universal power-law exponent of $\sim 1$, independent of data and channel statistics. This one over time training with superposition represents an up to tenfold acceleration compared to the purely sequential learning that takes place in the absence of superposition. Our finding that superposition leads to rapid training with a data-independent power law exponent may have important implications for a wide range of neural networks that employ superposition, including production-scale large language models.

The Blessing of Dimensionality in LLM Fine-tuning: A Variance-Curvature Perspective

Weight-perturbation evolution strategies (ES) can fine-tune billion-parameter language models with surprisingly small populations (e.g., $N\!\approx\!30$), contradicting classical zeroth-order curse-of-dimensionality intuition. We also observe a second seemingly separate phenomenon: under fixed hyperparameters, the stochastic fine-tuning reward often rises, peaks, and then degrades in both ES and GRPO. We argue that both effects reflect a shared geometric property of fine-tuning landscapes: they are low-dimensional in curvature. A small set of high-curvature dimensions dominates improvement, producing (i) heterogeneous time scales that yield rise-then-decay under fixed stochasticity, as captured by a minimal quadratic stochastic-ascent model, and (ii) degenerate improving updates, where many random perturbations share similar components along these directions. Using ES as a geometric probe on fine-tuning reward landscapes of GSM8K, ARC-C, and WinoGrande across Qwen2.5-Instruct models (0.5B--7B), we show that reward-improving perturbations remain empirically accessible with small populations across scales. Together, these results reconcile ES scalability with non-monotonic training dynamics and suggest that high-dimensional fine-tuning may admit a broader class of viable optimization methods than worst-case theory implies.

Beyond Pixel Simulation: Pathology Image Generation via Diagnostic Semantic Tokens and Prototype Control

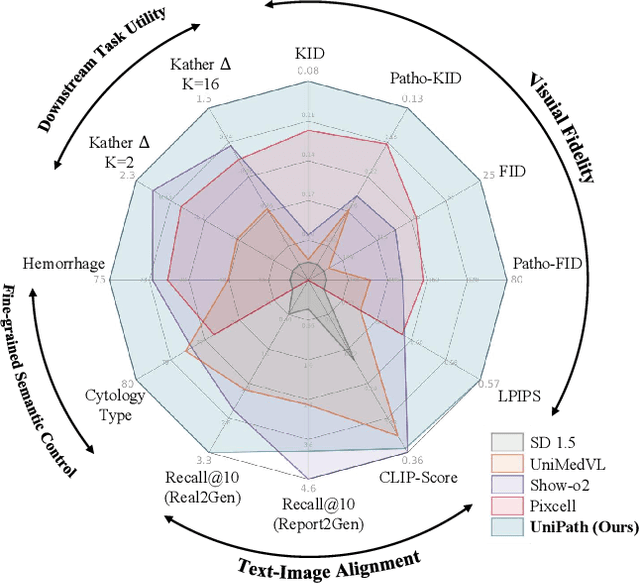
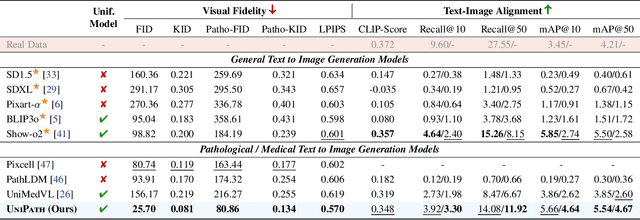
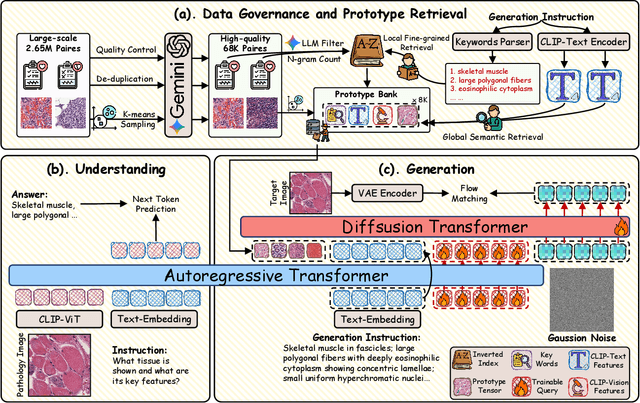
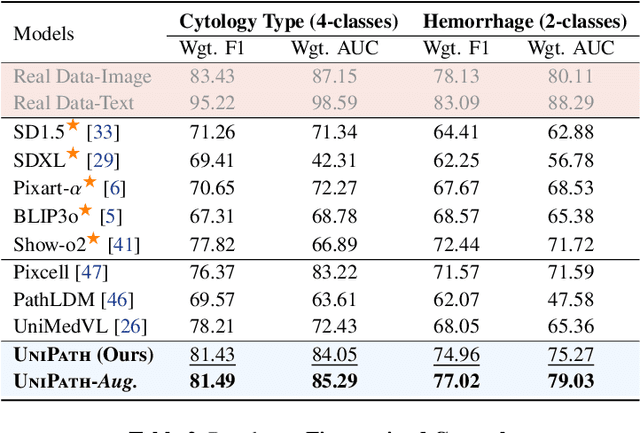
In computational pathology, understanding and generation have evolved along disparate paths: advanced understanding models already exhibit diagnostic-level competence, whereas generative models largely simulate pixels. Progress remains hindered by three coupled factors: the scarcity of large, high-quality image-text corpora; the lack of precise, fine-grained semantic control, which forces reliance on non-semantic cues; and terminological heterogeneity, where diverse phrasings for the same diagnostic concept impede reliable text conditioning. We introduce UniPath, a semantics-driven pathology image generation framework that leverages mature diagnostic understanding to enable controllable generation. UniPath implements Multi-Stream Control: a Raw-Text stream; a High-Level Semantics stream that uses learnable queries to a frozen pathology MLLM to distill paraphrase-robust Diagnostic Semantic Tokens and to expand prompts into diagnosis-aware attribute bundles; and a Prototype stream that affords component-level morphological control via a prototype bank. On the data front, we curate a 2.65M image-text corpus and a finely annotated, high-quality 68K subset to alleviate data scarcity. For a comprehensive assessment, we establish a four-tier evaluation hierarchy tailored to pathology. Extensive experiments demonstrate UniPath's SOTA performance, including a Patho-FID of 80.9 (51% better than the second-best) and fine-grained semantic control achieving 98.7% of the real-image. The meticulously curated datasets, complete source code, and pre-trained model weights developed in this study will be made openly accessible to the public.

Forging a Dynamic Memory: Retrieval-Guided Continual Learning for Generalist Medical Foundation Models

Multimodal biomedical Vision-Language Models (VLMs) exhibit immense potential in the field of Continual Learning (CL). However, they confront a core dilemma: how to preserve fine-grained intra-modality features while bridging the significant domain gap across different modalities. To address this challenge, we propose a comprehensive framework. Leveraging our 18-million multimodal and comprehensive medical retrieval database derived from PubMed scientific papers, we pioneer the integration of Retrieval-Augmented Generation (RAG) into CL. Specifically, we employ a multi-modal, multi-layer RAG system that provides real-time guidance for model fine-tuning through dynamic, on-demand knowledge retrieval. Building upon this, we introduce a dynamic knowledge distillation framework. This framework precisely resolves the aforementioned core dilemma by dynamically modulating the importance of the parameter space, the granularity of the distilled knowledge, and the data distribution of the reference dataset in accordance with the required level of detail. To thoroughly validate the clinical value of our strategy, we have designed a more rigorous \textbf{M}edical Generalist Task Incremental Learning (MGTIL) benchmark. This benchmark is engineered to simultaneously evaluate the model's capacity for adaptation to significant domain shifts, retention of subtle intra-domain features, and real-time learning of novel and complex medical tasks. Extensive experimental results demonstrate that our proposed method achieves state-of-the-art (SOTA) performance across all metrics. The code is provided in the supplementary materials.

FysicsWorld: A Unified Full-Modality Benchmark for Any-to-Any Understanding, Generation, and Reasoning

Despite rapid progress in multimodal large language models (MLLMs) and emerging omni-modal architectures, current benchmarks remain limited in scope and integration, suffering from incomplete modality coverage, restricted interaction to text-centric outputs, and weak interdependence and complementarity among modalities. To bridge these gaps, we introduce FysicsWorld, the first unified full-modality benchmark that supports bidirectional input-output across image, video, audio, and text, enabling comprehensive any-to-any evaluation across understanding, generation, and reasoning. FysicsWorld encompasses 16 primary tasks and 3,268 curated samples, aggregated from over 40 high-quality sources and covering a rich set of open-domain categories with diverse question types. We also propose the Cross-Modal Complementarity Screening (CMCS) strategy integrated in a systematic data construction framework that produces omni-modal data for spoken interaction and fusion-dependent cross-modal reasoning. Through a comprehensive evaluation of over 30 state-of-the-art baselines, spanning MLLMs, modality-specific models, unified understanding-generation models, and omni-modal language models, FysicsWorld exposes the performance disparities and limitations across models in understanding, generation, and reasoning. Our benchmark establishes a unified foundation and strong baselines for evaluating and advancing next-generation full-modality architectures.

Neural Thermodynamic Laws for Large Language Model Training

Beyond neural scaling laws, little is known about the laws underlying large language models (LLMs). We introduce Neural Thermodynamic Laws (NTL) -- a new framework that offers fresh insights into LLM training dynamics. On the theoretical side, we demonstrate that key thermodynamic quantities (e.g., temperature, entropy, heat capacity, thermal conduction) and classical thermodynamic principles (e.g., the three laws of thermodynamics and the equipartition theorem) naturally emerge under river-valley loss landscape assumptions. On the practical side, this scientific perspective yields intuitive guidelines for designing learning rate schedules.

VLM-based Prompts as the Optimal Assistant for Unpaired Histopathology Virtual Staining

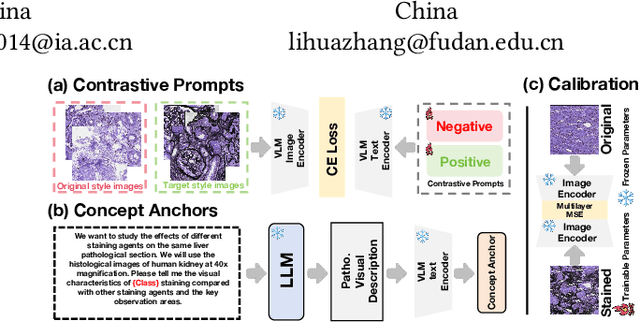
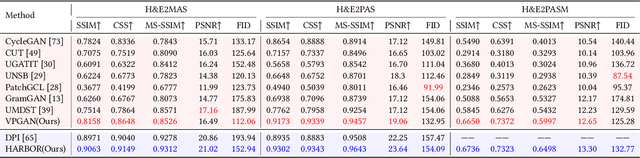
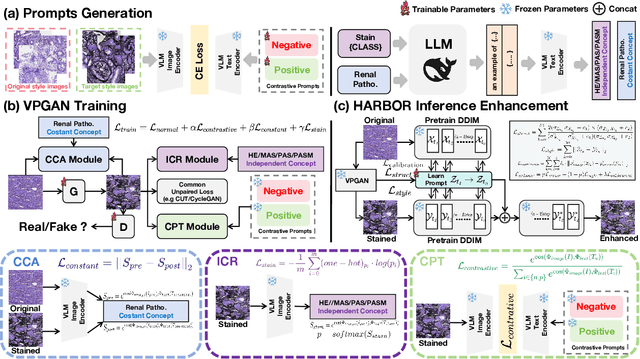
In histopathology, tissue sections are typically stained using common H&E staining or special stains (MAS, PAS, PASM, etc.) to clearly visualize specific tissue structures. The rapid advancement of deep learning offers an effective solution for generating virtually stained images, significantly reducing the time and labor costs associated with traditional histochemical staining. However, a new challenge arises in separating the fundamental visual characteristics of tissue sections from the visual differences induced by staining agents. Additionally, virtual staining often overlooks essential pathological knowledge and the physical properties of staining, resulting in only style-level transfer. To address these issues, we introduce, for the first time in virtual staining tasks, a pathological vision-language large model (VLM) as an auxiliary tool. We integrate contrastive learnable prompts, foundational concept anchors for tissue sections, and staining-specific concept anchors to leverage the extensive knowledge of the pathological VLM. This approach is designed to describe, frame, and enhance the direction of virtual staining. Furthermore, we have developed a data augmentation method based on the constraints of the VLM. This method utilizes the VLM's powerful image interpretation capabilities to further integrate image style and structural information, proving beneficial in high-precision pathological diagnostics. Extensive evaluations on publicly available multi-domain unpaired staining datasets demonstrate that our method can generate highly realistic images and enhance the accuracy of downstream tasks, such as glomerular detection and segmentation. Our code is available at: https://github.com/CZZZZZZZZZZZZZZZZZ/VPGAN-HARBOR

Physics of Skill Learning

We aim to understand physics of skill learning, i.e., how skills are learned in neural networks during training. We start by observing the Domino effect, i.e., skills are learned sequentially, and notably, some skills kick off learning right after others complete learning, similar to the sequential fall of domino cards. To understand the Domino effect and relevant behaviors of skill learning, we take physicists' approach of abstraction and simplification. We propose three models with varying complexities -- the Geometry model, the Resource model, and the Domino model, trading between reality and simplicity. The Domino effect can be reproduced in the Geometry model, whose resource interpretation inspires the Resource model, which can be further simplified to the Domino model. These models present different levels of abstraction and simplification; each is useful to study some aspects of skill learning. The Geometry model provides interesting insights into neural scaling laws and optimizers; the Resource model sheds light on the learning dynamics of compositional tasks; the Domino model reveals the benefits of modularity. These models are not only conceptually interesting -- e.g., we show how Chinchilla scaling laws can emerge from the Geometry model, but also are useful in practice by inspiring algorithmic development -- e.g., we show how simple algorithmic changes, motivated by these toy models, can speed up the training of deep learning models.