Probing for Arithmetic Errors in Language Models

We investigate whether internal activations in language models can be used to detect arithmetic errors. Starting with a controlled setting of 3-digit addition, we show that simple probes can accurately decode both the model's predicted output and the correct answer from hidden states, regardless of whether the model's output is correct. Building on this, we train lightweight error detectors that predict model correctness with over 90% accuracy. We then extend our analysis to structured chain-of-thought traces on addition-only GSM8K problems and find that probes trained on simple arithmetic generalize well to this more complex setting, revealing consistent internal representations. Finally, we demonstrate that these probes can guide selective re-prompting of erroneous reasoning steps, improving task accuracy with minimal disruption to correct outputs. Our findings suggest that arithmetic errors can be anticipated from internal activations alone, and that simple probes offer a viable path toward lightweight model self-correction.

Dense SAE Latents Are Features, Not Bugs

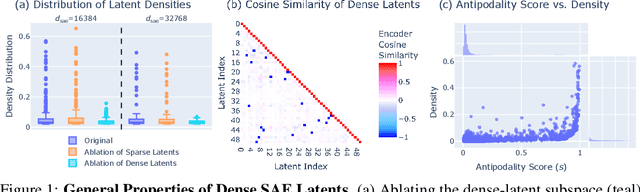
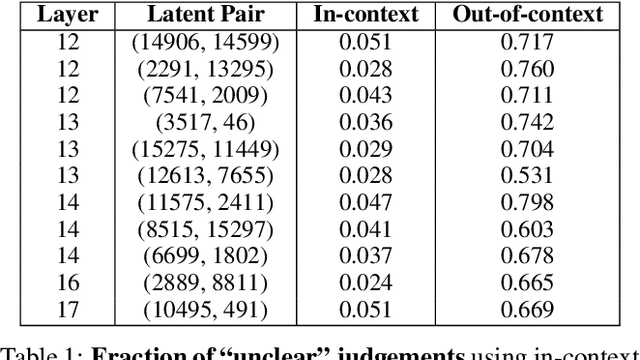
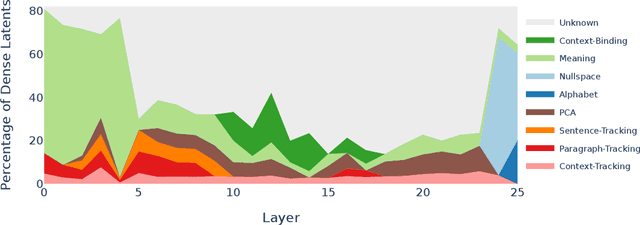
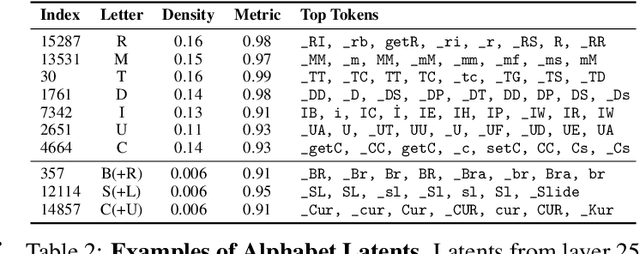
Sparse autoencoders (SAEs) are designed to extract interpretable features from language models by enforcing a sparsity constraint. Ideally, training an SAE would yield latents that are both sparse and semantically meaningful. However, many SAE latents activate frequently (i.e., are \emph{dense}), raising concerns that they may be undesirable artifacts of the training procedure. In this work, we systematically investigate the geometry, function, and origin of dense latents and show that they are not only persistent but often reflect meaningful model representations. We first demonstrate that dense latents tend to form antipodal pairs that reconstruct specific directions in the residual stream, and that ablating their subspace suppresses the emergence of new dense features in retrained SAEs -- suggesting that high density features are an intrinsic property of the residual space. We then introduce a taxonomy of dense latents, identifying classes tied to position tracking, context binding, entropy regulation, letter-specific output signals, part-of-speech, and principal component reconstruction. Finally, we analyze how these features evolve across layers, revealing a shift from structural features in early layers, to semantic features in mid layers, and finally to output-oriented signals in the last layers of the model. Our findings indicate that dense latents serve functional roles in language model computation and should not be dismissed as training noise.

Transferring Features Across Language Models With Model Stitching

In this work, we demonstrate that affine mappings between residual streams of language models is a cheap way to effectively transfer represented features between models. We apply this technique to transfer the weights of Sparse Autoencoders (SAEs) between models of different sizes to compare their representations. We find that small and large models learn highly similar representation spaces, which motivates training expensive components like SAEs on a smaller model and transferring to a larger model at a FLOPs savings. For example, using a small-to-large transferred SAE as initialization can lead to 50% cheaper training runs when training SAEs on larger models. Next, we show that transferred probes and steering vectors can effectively recover ground truth performance. Finally, we dive deeper into feature-level transferability, finding that semantic and structural features transfer noticeably differently while specific classes of functional features have their roles faithfully mapped. Overall, our findings illustrate similarities and differences in the linear representation spaces of small and large models and demonstrate a method for improving the training efficiency of SAEs.

MIB: A Mechanistic Interpretability Benchmark

How can we know whether new mechanistic interpretability methods achieve real improvements? In pursuit of meaningful and lasting evaluation standards, we propose MIB, a benchmark with two tracks spanning four tasks and five models. MIB favors methods that precisely and concisely recover relevant causal pathways or specific causal variables in neural language models. The circuit localization track compares methods that locate the model components - and connections between them - most important for performing a task (e.g., attribution patching or information flow routes). The causal variable localization track compares methods that featurize a hidden vector, e.g., sparse autoencoders (SAEs) or distributed alignment search (DAS), and locate model features for a causal variable relevant to the task. Using MIB, we find that attribution and mask optimization methods perform best on circuit localization. For causal variable localization, we find that the supervised DAS method performs best, while SAE features are not better than neurons, i.e., standard dimensions of hidden vectors. These findings illustrate that MIB enables meaningful comparisons of methods, and increases our confidence that there has been real progress in the field.

Confidence Regulation Neurons in Language Models

Despite their widespread use, the mechanisms by which large language models (LLMs) represent and regulate uncertainty in next-token predictions remain largely unexplored. This study investigates two critical components believed to influence this uncertainty: the recently discovered entropy neurons and a new set of components that we term token frequency neurons. Entropy neurons are characterized by an unusually high weight norm and influence the final layer normalization (LayerNorm) scale to effectively scale down the logits. Our work shows that entropy neurons operate by writing onto an unembedding null space, allowing them to impact the residual stream norm with minimal direct effect on the logits themselves. We observe the presence of entropy neurons across a range of models, up to 7 billion parameters. On the other hand, token frequency neurons, which we discover and describe here for the first time, boost or suppress each token's logit proportionally to its log frequency, thereby shifting the output distribution towards or away from the unigram distribution. Finally, we present a detailed case study where entropy neurons actively manage confidence in the setting of induction, i.e. detecting and continuing repeated subsequences.

Groundedness in Retrieval-augmented Long-form Generation: An Empirical Study

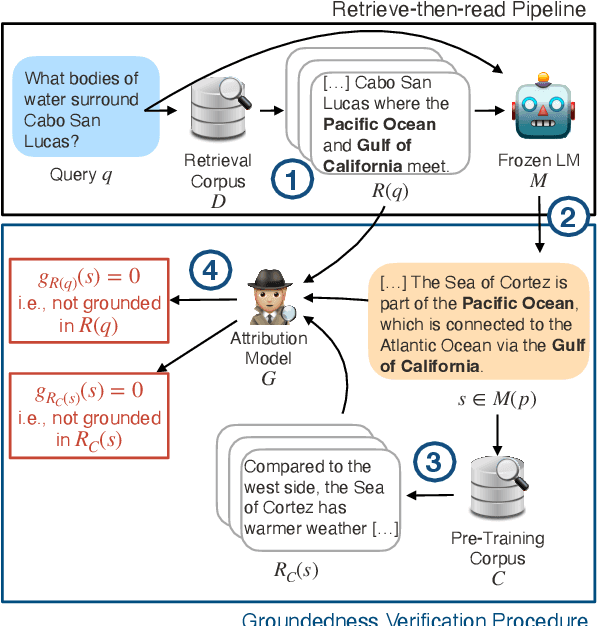
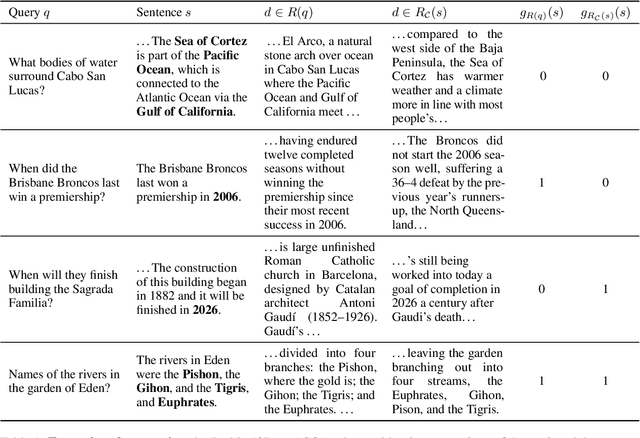
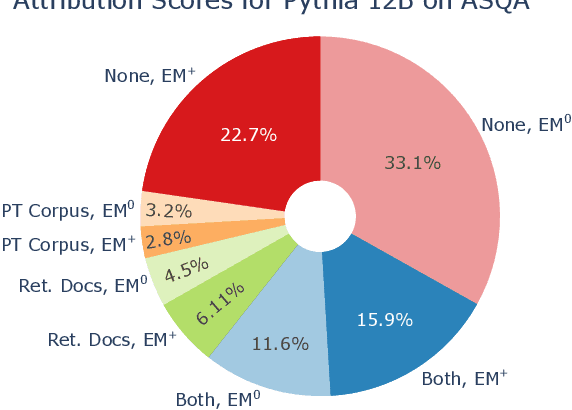
We present an empirical study of groundedness in long-form question answering (LFQA) by retrieval-augmented large language models (LLMs). In particular, we evaluate whether every generated sentence is grounded in the retrieved documents or the model's pre-training data. Across 3 datasets and 4 model families, our findings reveal that a significant fraction of generated sentences are consistently ungrounded, even when those sentences contain correct ground-truth answers. Additionally, we examine the impacts of factors such as model size, decoding strategy, and instruction tuning on groundedness. Our results show that while larger models tend to ground their outputs more effectively, a significant portion of correct answers remains compromised by hallucinations. This study provides novel insights into the groundedness challenges in LFQA and underscores the necessity for more robust mechanisms in LLMs to mitigate the generation of ungrounded content.

Do Language Models Exhibit the Same Cognitive Biases in Problem Solving as Human Learners?

There is increasing interest in employing large language models (LLMs) as cognitive models. For such purposes, it is central to understand which cognitive properties are well-modeled by LLMs, and which are not. In this work, we study the biases of LLMs in relation to those known in children when solving arithmetic word problems. Surveying the learning science literature, we posit that the problem-solving process can be split into three distinct steps: text comprehension, solution planning and solution execution. We construct tests for each one in order to understand which parts of this process can be faithfully modeled by current state-of-the-art LLMs. We generate a novel set of word problems for each of these tests, using a neuro-symbolic method that enables fine-grained control over the problem features. We find evidence that LLMs, with and without instruction-tuning, exhibit human-like biases in both the text-comprehension and the solution-planning steps of the solving process, but not during the final step which relies on the problem's arithmetic expressions (solution execution).

Towards a Mechanistic Interpretation of Multi-Step Reasoning Capabilities of Language Models

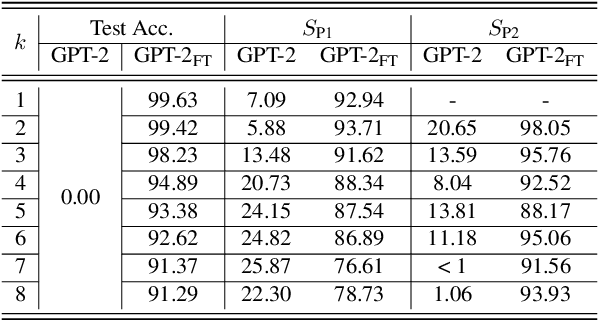
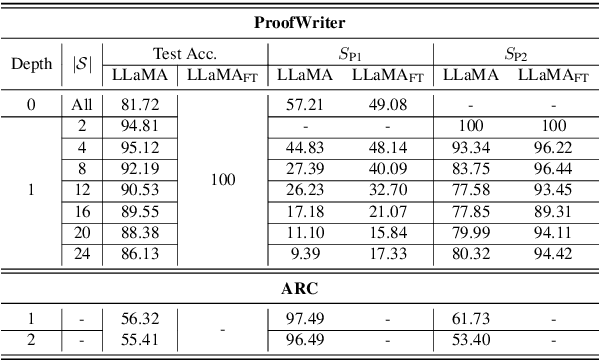
Recent work has shown that language models (LMs) have strong multi-step (i.e., procedural) reasoning capabilities. However, it is unclear whether LMs perform these tasks by cheating with answers memorized from pretraining corpus, or, via a multi-step reasoning mechanism. In this paper, we try to answer this question by exploring a mechanistic interpretation of LMs for multi-step reasoning tasks. Concretely, we hypothesize that the LM implicitly embeds a reasoning tree resembling the correct reasoning process within it. We test this hypothesis by introducing a new probing approach (called MechanisticProbe) that recovers the reasoning tree from the model's attention patterns. We use our probe to analyze two LMs: GPT-2 on a synthetic task (k-th smallest element), and LLaMA on two simple language-based reasoning tasks (ProofWriter & AI2 Reasoning Challenge). We show that MechanisticProbe is able to detect the information of the reasoning tree from the model's attentions for most examples, suggesting that the LM indeed is going through a process of multi-step reasoning within its architecture in many cases.

Understanding Arithmetic Reasoning in Language Models using Causal Mediation Analysis

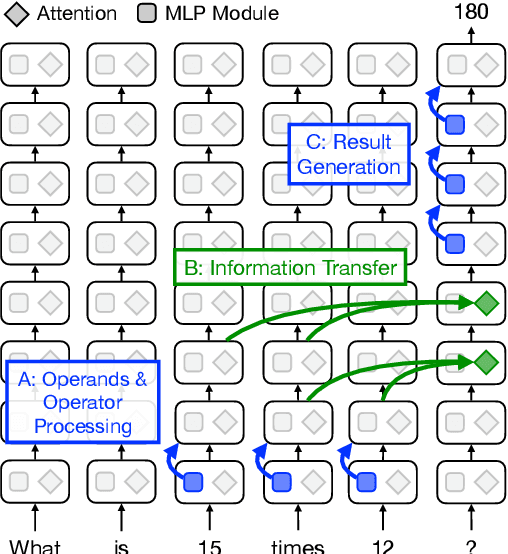
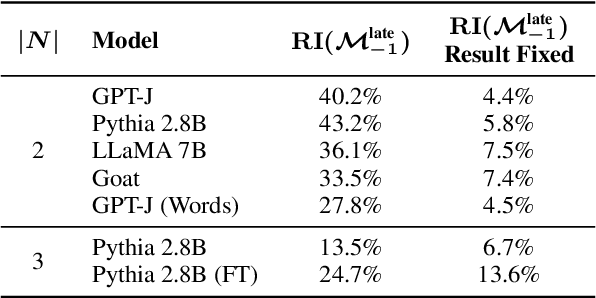
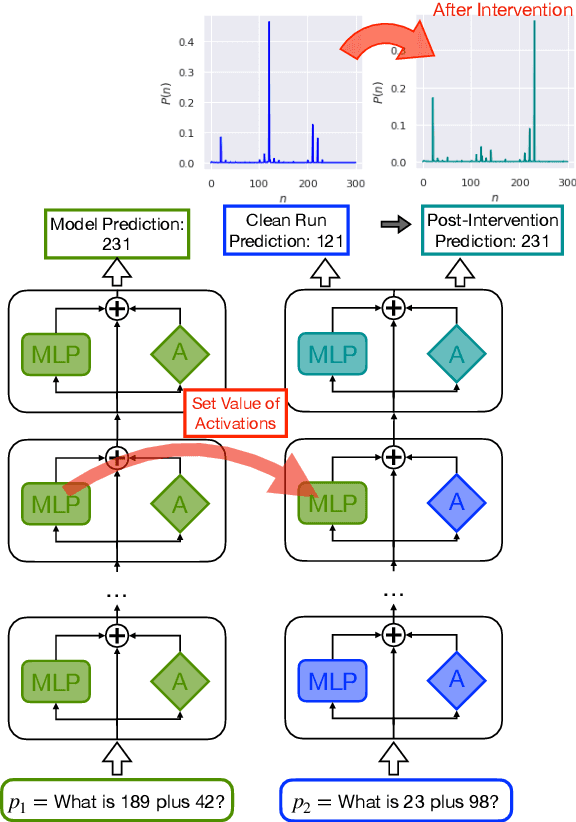
Mathematical reasoning in large language models (LLMs) has garnered attention in recent research, but there is limited understanding of how these models process and store information related to arithmetic tasks. In this paper, we present a mechanistic interpretation of LLMs for arithmetic-based questions using a causal mediation analysis framework. By intervening on the activations of specific model components and measuring the resulting changes in predicted probabilities, we identify the subset of parameters responsible for specific predictions. We analyze two pre-trained language models with different sizes (2.8B and 6B parameters). Experimental results reveal that a small set of mid-late layers significantly affect predictions for arithmetic-based questions, with distinct activation patterns for correct and wrong predictions. We also investigate the role of the attention mechanism and compare the model's activation patterns for arithmetic queries with the prediction of factual knowledge. Our findings provide insights into the mechanistic interpretation of LLMs for arithmetic tasks and highlight the specific components involved in arithmetic reasoning.

Distilling Multi-Step Reasoning Capabilities of Large Language Models into Smaller Models via Semantic Decompositions

Step-by-step reasoning approaches like chain-of-thought (CoT) have proved to be a very effective technique to induce reasoning capabilities in large language models. However, the success of the CoT approach depends primarily on model size, and often billion parameter-scale models are needed to get CoT to work. In this paper, we propose a knowledge distillation approach, that leverages the step-by-step CoT reasoning capabilities of larger models and distils these reasoning abilities into smaller models. Our approach Decompositional Distillation learns a semantic decomposition of the original problem into a sequence of subproblems and uses it to train two models: a) a problem decomposer that learns to decompose the complex reasoning problem into a sequence of simpler sub-problems and b) a problem solver that uses the intermediate subproblems to solve the overall problem. On a multi-step math word problem dataset (GSM8K), we boost the performance of GPT-2 variants up to 35% when distilled with our approach compared to CoT. We show that using our approach, it is possible to train a GPT-2-large model (775M) that can outperform a 10X larger GPT-3 (6B) model trained using CoT reasoning. Finally, we also demonstrate that our approach of problem decomposition can also be used as an alternative to CoT prompting, which boosts the GPT-3 performance by 40% compared to CoT prompts.