Kumar Shridhar
Shammie
Apertus: Democratizing Open and Compliant LLMs for Global Language Environments
Sep 17, 2025
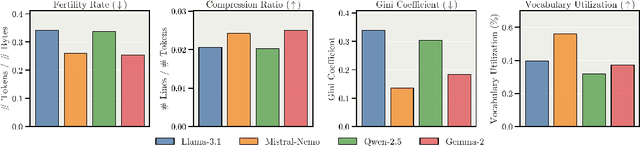

Abstract:We present Apertus, a fully open suite of large language models (LLMs) designed to address two systemic shortcomings in today's open model ecosystem: data compliance and multilingual representation. Unlike many prior models that release weights without reproducible data pipelines or regard for content-owner rights, Apertus models are pretrained exclusively on openly available data, retroactively respecting robots.txt exclusions and filtering for non-permissive, toxic, and personally identifiable content. To mitigate risks of memorization, we adopt the Goldfish objective during pretraining, strongly suppressing verbatim recall of data while retaining downstream task performance. The Apertus models also expand multilingual coverage, training on 15T tokens from over 1800 languages, with ~40% of pretraining data allocated to non-English content. Released at 8B and 70B scales, Apertus approaches state-of-the-art results among fully open models on multilingual benchmarks, rivalling or surpassing open-weight counterparts. Beyond model weights, we release all scientific artifacts from our development cycle with a permissive license, including data preparation scripts, checkpoints, evaluation suites, and training code, enabling transparent audit and extension.
EMAFusion: A Self-Optimizing System for Seamless LLM Selection and Integration
Apr 14, 2025Abstract:While recent advances in large language models (LLMs) have significantly enhanced performance across diverse natural language tasks, the high computational and financial costs associated with their deployment remain substantial barriers. Existing routing strategies partially alleviate this challenge by assigning queries to cheaper or specialized models, but they frequently rely on extensive labeled data or fragile task-specific heuristics. Conversely, fusion techniques aggregate multiple LLM outputs to boost accuracy and robustness, yet they often exacerbate cost and may reinforce shared biases. We introduce EMAFusion, a new framework that self-optimizes for seamless LLM selection and reliable execution for a given query. Specifically, EMAFusion integrates a taxonomy-based router for familiar query types, a learned router for ambiguous inputs, and a cascading approach that progressively escalates from cheaper to more expensive models based on multi-judge confidence evaluations. Through extensive evaluations, we find EMAFusion outperforms the best individual models by over 2.6 percentage points (94.3% vs. 91.7%), while being 4X cheaper than the average cost. EMAFusion further achieves a remarkable 17.1 percentage point improvement over models like GPT-4 at less than 1/20th the cost. Our combined routing approach delivers 94.3% accuracy compared to taxonomy-based (88.1%) and learned model predictor-based (91.7%) methods alone, demonstrating the effectiveness of our unified strategy. Finally, EMAFusion supports flexible cost-accuracy trade-offs, allowing users to balance their budgetary constraints and performance needs.
UNDO: Understanding Distillation as Optimization
Apr 03, 2025Abstract:Knowledge distillation has emerged as an effective strategy for compressing large language models' (LLMs) knowledge into smaller, more efficient student models. However, standard one-shot distillation methods often produce suboptimal results due to a mismatch between teacher-generated rationales and the student's specific learning requirements. In this paper, we introduce the UNDO: UNderstanding Distillation as Optimization framework, designed to bridge this gap by iteratively identifying the student's errors and prompting the teacher to refine its explanations accordingly. Each iteration directly targets the student's learning deficiencies, motivating the teacher to provide tailored and enhanced rationales that specifically address these weaknesses. Empirical evaluations on various challenging mathematical and commonsense reasoning tasks demonstrate that our iterative distillation method, UNDO, significantly outperforms standard one-step distillation methods, achieving performance gains of up to 20%. Additionally, we show that teacher-generated data refined through our iterative process remains effective even when applied to different student models, underscoring the broad applicability of our approach. Our work fundamentally reframes knowledge distillation as an iterative teacher-student interaction, effectively leveraging dynamic refinement by the teacher for better knowledge distillation.
Beyond Pattern Recognition: Probing Mental Representations of LMs
Feb 23, 2025



Abstract:Language Models (LMs) have demonstrated impressive capabilities in solving complex reasoning tasks, particularly when prompted to generate intermediate explanations. However, it remains an open question whether these intermediate reasoning traces represent a dynamic, evolving thought process or merely reflect sophisticated pattern recognition acquired during large scale pre training. Drawing inspiration from human cognition, where reasoning unfolds incrementally as new information is assimilated and internal models are continuously updated, we propose to delve deeper into the mental model of various LMs. We propose a new way to assess the mental modeling of LMs, where they are provided with problem details gradually, allowing each new piece of data to build upon and refine the model's internal representation of the task. We systematically compare this step by step mental modeling strategy with traditional full prompt methods across both text only and vision and text modalities. Experiments on the MathWorld dataset across different model sizes and problem complexities confirm that both text-based LLMs and multimodal LMs struggle to create mental representations, questioning how their internal cognitive processes work.
SIKeD: Self-guided Iterative Knowledge Distillation for mathematical reasoning
Oct 24, 2024Abstract:Large Language Models (LLMs) can transfer their reasoning skills to smaller models by teaching them to generate the intermediate reasoning process required to solve multistep reasoning tasks. While LLMs can accurately solve reasoning tasks through a variety of strategies, even without fine-tuning, smaller models are not expressive enough to fit the LLMs distribution on all strategies when distilled and tend to prioritize one strategy over the others. This reliance on one strategy poses a challenge for smaller models when attempting to solve reasoning tasks that may be difficult with their preferred strategy. To address this, we propose a distillation method SIKeD (Self-guided Iterative Knowledge Distillation for mathematical reasoning), where the LLM teaches the smaller model to approach a task using different strategies and the smaller model uses its self-generated on-policy outputs to choose the most suitable strategy for the given task. The training continues in a self-guided iterative manner, where for each training iteration, a decision is made on how to combine the LLM data with the self-generated outputs. Unlike traditional distillation methods, SIKeD allows the smaller model to learn which strategy is suitable for a given task while continuously learning to solve a task using different strategies. Our experiments on various mathematical reasoning datasets show that SIKeD significantly outperforms traditional distillation techniques across smaller models of different sizes. Our code is available at: https://github.com/kumar-shridhar/SIKeD
SMART: Self-learning Meta-strategy Agent for Reasoning Tasks
Oct 21, 2024Abstract:Tasks requiring deductive reasoning, especially those involving multiple steps, often demand adaptive strategies such as intermediate generation of rationales or programs, as no single approach is universally optimal. While Language Models (LMs) can enhance their outputs through iterative self-refinement and strategy adjustments, they frequently fail to apply the most effective strategy in their first attempt. This inefficiency raises the question: Can LMs learn to select the optimal strategy in the first attempt, without a need for refinement? To address this challenge, we introduce SMART (Self-learning Meta-strategy Agent for Reasoning Tasks), a novel framework that enables LMs to autonomously learn and select the most effective strategies for various reasoning tasks. We model the strategy selection process as a Markov Decision Process and leverage reinforcement learning-driven continuous self-improvement to allow the model to find the suitable strategy to solve a given task. Unlike traditional self-refinement methods that rely on multiple inference passes or external feedback, SMART allows an LM to internalize the outcomes of its own reasoning processes and adjust its strategy accordingly, aiming for correct solutions on the first attempt. Our experiments across various reasoning datasets and with different model architectures demonstrate that SMART significantly enhances the ability of models to choose optimal strategies without external guidance (+15 points on the GSM8K dataset). By achieving higher accuracy with a single inference pass, SMART not only improves performance but also reduces computational costs for refinement-based strategies, paving the way for more efficient and intelligent reasoning in LMs.
Calibrating Large Language Models with Sample Consistency
Feb 21, 2024Abstract:Accurately gauging the confidence level of Large Language Models' (LLMs) predictions is pivotal for their reliable application. However, LLMs are often uncalibrated inherently and elude conventional calibration techniques due to their proprietary nature and massive scale. In this work, we explore the potential of deriving confidence from the distribution of multiple randomly sampled model generations, via three measures of consistency. We perform an extensive evaluation across various open and closed-source models on nine reasoning datasets. Results show that consistency-based calibration methods outperform existing post-hoc approaches. Meanwhile, we find that factors such as intermediate explanations, model scaling, and larger sample sizes enhance calibration, while instruction-tuning makes calibration more difficult. Moreover, confidence scores obtained from consistency have the potential to enhance model performance. Finally, we offer practical guidance on choosing suitable consistency metrics for calibration, tailored to the characteristics of various LMs.
Distilling LLMs' Decomposition Abilities into Compact Language Models
Feb 02, 2024Abstract:Large Language Models (LLMs) have demonstrated proficiency in their reasoning abilities, yet their large size presents scalability challenges and limits any further customization. In contrast, compact models offer customized training but often fall short in solving complex reasoning tasks. This study focuses on distilling the LLMs' decomposition skills into compact models using offline reinforcement learning. We leverage the advancements in the LLM`s capabilities to provide feedback and generate a specialized task-specific dataset for training compact models. The development of an AI-generated dataset and the establishment of baselines constitute the primary contributions of our work, underscoring the potential of compact models in replicating complex problem-solving skills.
The ART of LLM Refinement: Ask, Refine, and Trust
Nov 14, 2023

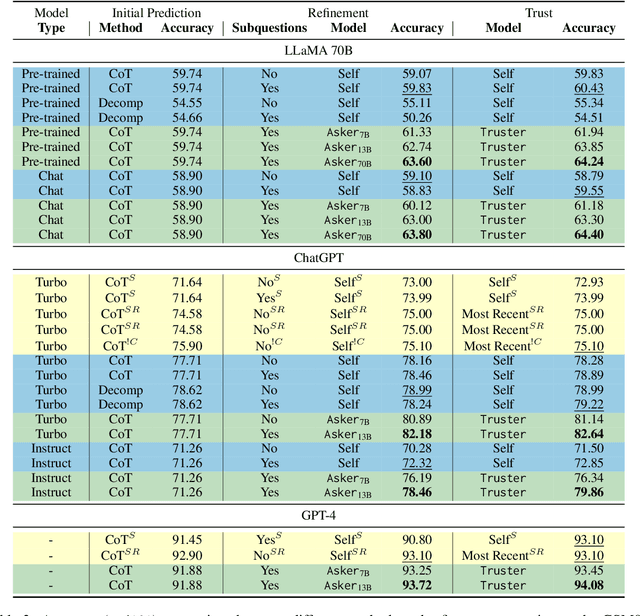

Abstract:In recent years, Large Language Models (LLMs) have demonstrated remarkable generative abilities, but can they judge the quality of their own generations? A popular concept, referred to as self-refinement, postulates that LLMs can detect and correct the errors in their generations when asked to do so. However, recent empirical evidence points in the opposite direction, suggesting that LLMs often struggle to accurately identify errors when reasoning is involved. To address this, we propose a reasoning with refinement objective called ART: Ask, Refine, and Trust, which asks necessary questions to decide when an LLM should refine its output, and either affirm or withhold trust in its refinement by ranking the refinement and the initial prediction. On two multistep reasoning tasks of mathematical word problems (GSM8K) and question answering (StrategyQA), ART achieves a performance gain of +5 points over self-refinement baselines, while using a much smaller model as the decision maker. We also demonstrate the benefit of using smaller models to make refinement decisions as a cost-effective alternative to fine-tuning a larger model.
First Step Advantage: Importance of Starting Right in Multi-Step Reasoning
Nov 14, 2023


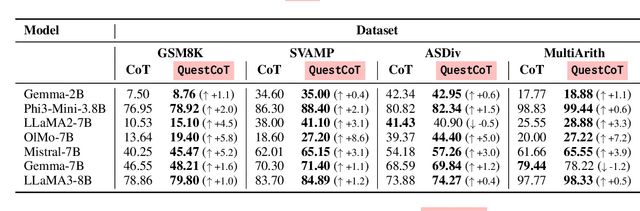
Abstract:Large Language Models (LLMs) can solve complex reasoning tasks by generating rationales for their predictions. Distilling these capabilities into a smaller, compact model can facilitate the creation of specialized, cost-effective models tailored for specific tasks. However, smaller models often face challenges in complex reasoning tasks and often deviate from the correct reasoning path. We show that LLMs can guide smaller models and bring them back to the correct reasoning path only if they intervene at the right time. We show that smaller models fail to reason primarily due to their difficulty in initiating the process, and that guiding them in the right direction can lead to a performance gain of over 100%. We explore different model sizes and evaluate the benefits of providing guidance to improve reasoning in smaller models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge