Barna Pasztor
Apertus: Democratizing Open and Compliant LLMs for Global Language Environments
Sep 17, 2025
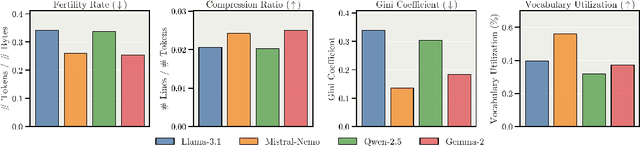

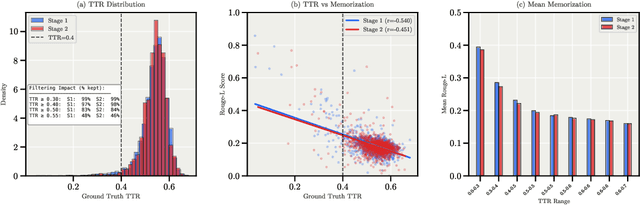
Abstract:We present Apertus, a fully open suite of large language models (LLMs) designed to address two systemic shortcomings in today's open model ecosystem: data compliance and multilingual representation. Unlike many prior models that release weights without reproducible data pipelines or regard for content-owner rights, Apertus models are pretrained exclusively on openly available data, retroactively respecting robots.txt exclusions and filtering for non-permissive, toxic, and personally identifiable content. To mitigate risks of memorization, we adopt the Goldfish objective during pretraining, strongly suppressing verbatim recall of data while retaining downstream task performance. The Apertus models also expand multilingual coverage, training on 15T tokens from over 1800 languages, with ~40% of pretraining data allocated to non-English content. Released at 8B and 70B scales, Apertus approaches state-of-the-art results among fully open models on multilingual benchmarks, rivalling or surpassing open-weight counterparts. Beyond model weights, we release all scientific artifacts from our development cycle with a permissive license, including data preparation scripts, checkpoints, evaluation suites, and training code, enabling transparent audit and extension.
Stochastic Bilevel Optimization with Lower-Level Contextual Markov Decision Processes
Jun 03, 2024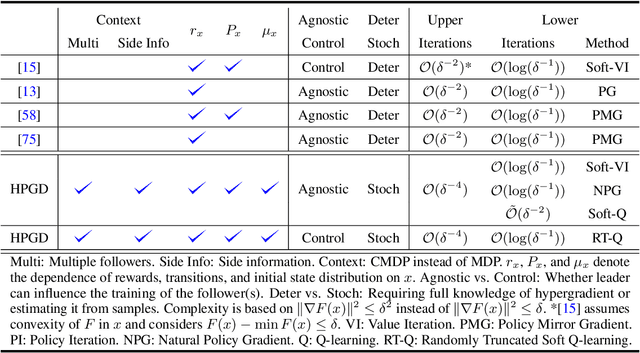
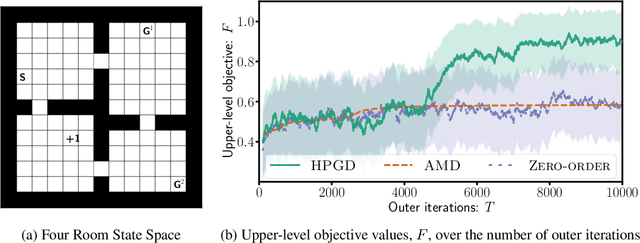

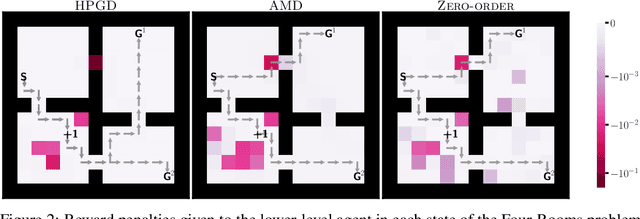
Abstract:In various applications, the optimal policy in a strategic decision-making problem depends both on the environmental configuration and exogenous events. For these settings, we introduce Bilevel Optimization with Contextual Markov Decision Processes (BO-CMDP), a stochastic bilevel decision-making model, where the lower level consists of solving a contextual Markov Decision Process (CMDP). BO-CMDP can be viewed as a Stackelberg Game where the leader and a random context beyond the leader's control together decide the setup of (many) MDPs that (potentially multiple) followers best respond to. This framework extends beyond traditional bilevel optimization and finds relevance in diverse fields such as model design for MDPs, tax design, reward shaping and dynamic mechanism design. We propose a stochastic Hyper Policy Gradient Descent (HPGD) algorithm to solve BO-CMDP, and demonstrate its convergence. Notably, HPGD only utilizes observations of the followers' trajectories. Therefore, it allows followers to use any training procedure and the leader to be agnostic of the specific algorithm used, which aligns with various real-world scenarios. We further consider the setting when the leader can influence the training of followers and propose an accelerated algorithm. We empirically demonstrate the performance of our algorithm.
Efficient Model-Based Multi-Agent Mean-Field Reinforcement Learning
Jul 08, 2021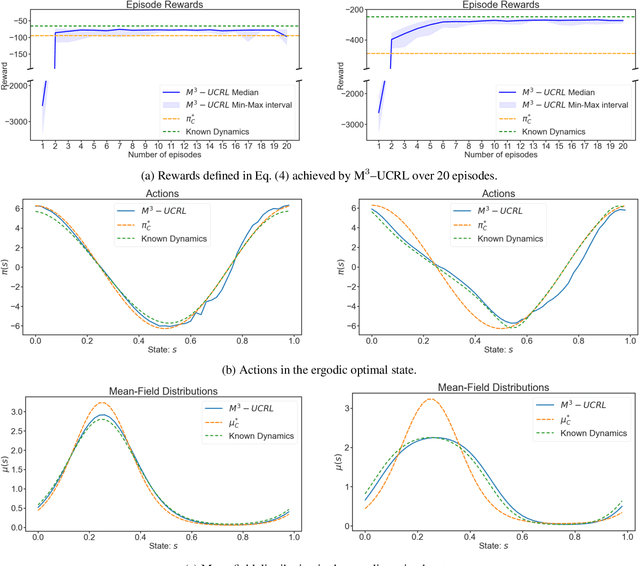
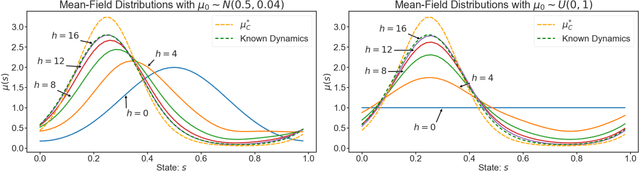
Abstract:Learning in multi-agent systems is highly challenging due to the inherent complexity introduced by agents' interactions. We tackle systems with a huge population of interacting agents (e.g., swarms) via Mean-Field Control (MFC). MFC considers an asymptotically infinite population of identical agents that aim to collaboratively maximize the collective reward. Specifically, we consider the case of unknown system dynamics where the goal is to simultaneously optimize for the rewards and learn from experience. We propose an efficient model-based reinforcement learning algorithm $\text{M}^3\text{-UCRL}$ that runs in episodes and provably solves this problem. $\text{M}^3\text{-UCRL}$ uses upper-confidence bounds to balance exploration and exploitation during policy learning. Our main theoretical contributions are the first general regret bounds for model-based RL for MFC, obtained via a novel mean-field type analysis. $\text{M}^3\text{-UCRL}$ can be instantiated with different models such as neural networks or Gaussian Processes, and effectively combined with neural network policy learning. We empirically demonstrate the convergence of $\text{M}^3\text{-UCRL}$ on the swarm motion problem of controlling an infinite population of agents seeking to maximize location-dependent reward and avoid congested areas.
Stochastic Gradient Descent Works Really Well for Stress Minimization
Aug 24, 2020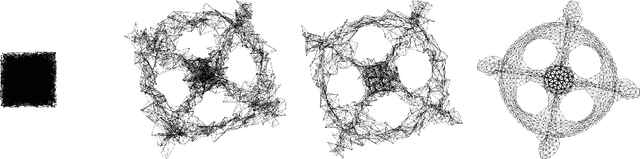
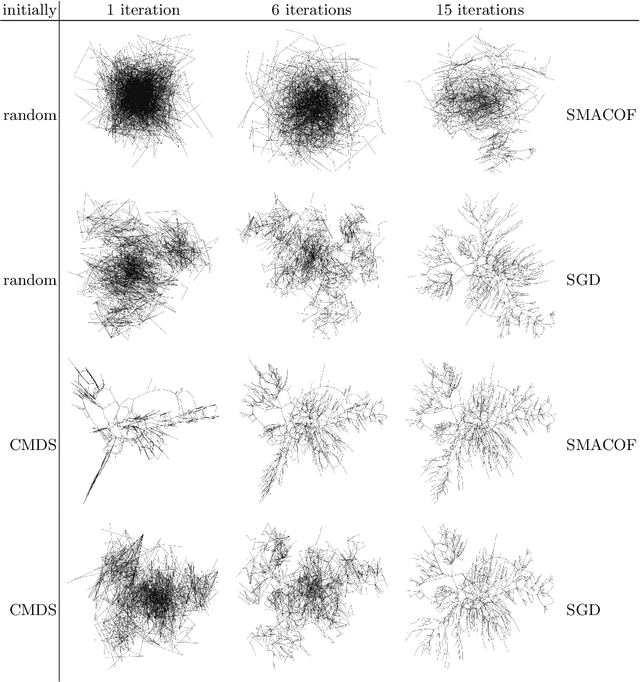
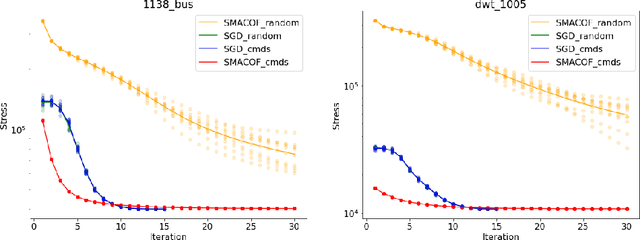
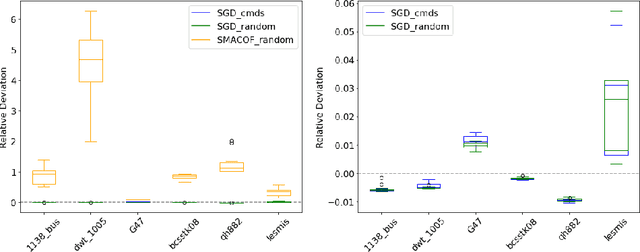
Abstract:Stress minimization is among the best studied force-directed graph layout methods because it reliably yields high-quality layouts. It thus comes as a surprise that a novel approach based on stochastic gradient descent (Zheng, Pawar and Goodman, TVCG 2019) is claimed to improve on state-of-the-art approaches based on majorization. We present experimental evidence that the new approach does not actually yield better layouts, but that it is still to be preferred because it is simpler and robust against poor initialization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge