Efficient Model-Based Multi-Agent Mean-Field Reinforcement Learning
Paper and Code
Jul 08, 2021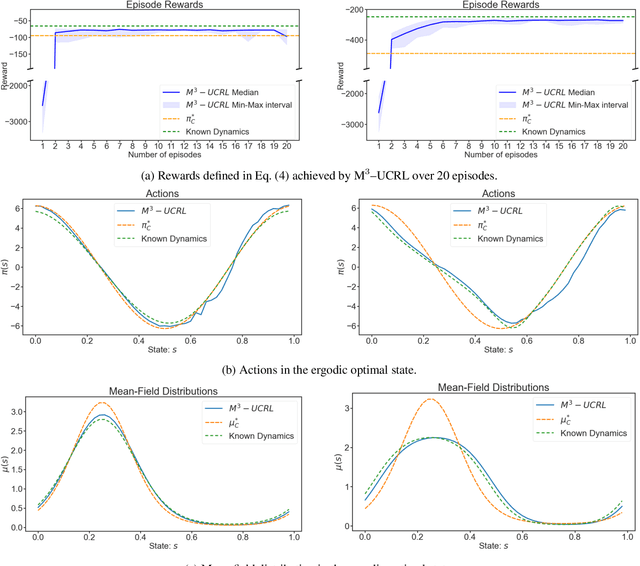
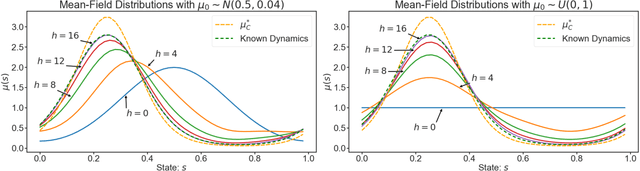
Learning in multi-agent systems is highly challenging due to the inherent complexity introduced by agents' interactions. We tackle systems with a huge population of interacting agents (e.g., swarms) via Mean-Field Control (MFC). MFC considers an asymptotically infinite population of identical agents that aim to collaboratively maximize the collective reward. Specifically, we consider the case of unknown system dynamics where the goal is to simultaneously optimize for the rewards and learn from experience. We propose an efficient model-based reinforcement learning algorithm $\text{M}^3\text{-UCRL}$ that runs in episodes and provably solves this problem. $\text{M}^3\text{-UCRL}$ uses upper-confidence bounds to balance exploration and exploitation during policy learning. Our main theoretical contributions are the first general regret bounds for model-based RL for MFC, obtained via a novel mean-field type analysis. $\text{M}^3\text{-UCRL}$ can be instantiated with different models such as neural networks or Gaussian Processes, and effectively combined with neural network policy learning. We empirically demonstrate the convergence of $\text{M}^3\text{-UCRL}$ on the swarm motion problem of controlling an infinite population of agents seeking to maximize location-dependent reward and avoid congested areas.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge