Scalable Neural Incentive Design with Parameterized Mean-Field Approximation

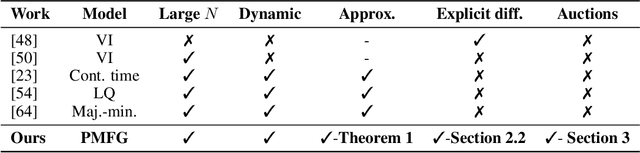
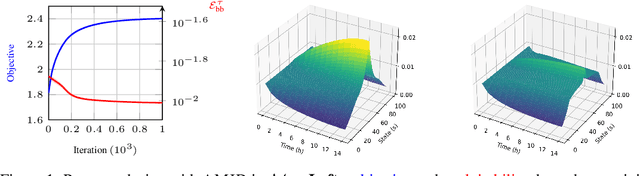
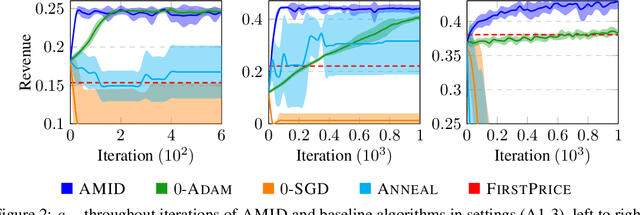
Designing incentives for a multi-agent system to induce a desirable Nash equilibrium is both a crucial and challenging problem appearing in many decision-making domains, especially for a large number of agents $N$. Under the exchangeability assumption, we formalize this incentive design (ID) problem as a parameterized mean-field game (PMFG), aiming to reduce complexity via an infinite-population limit. We first show that when dynamics and rewards are Lipschitz, the finite-$N$ ID objective is approximated by the PMFG at rate $\mathscr{O}(\frac{1}{\sqrt{N}})$. Moreover, beyond the Lipschitz-continuous setting, we prove the same $\mathscr{O}(\frac{1}{\sqrt{N}})$ decay for the important special case of sequential auctions, despite discontinuities in dynamics, through a tailored auction-specific analysis. Built on our novel approximation results, we further introduce our Adjoint Mean-Field Incentive Design (AMID) algorithm, which uses explicit differentiation of iterated equilibrium operators to compute gradients efficiently. By uniting approximation bounds with optimization guarantees, AMID delivers a powerful, scalable algorithmic tool for many-agent (large $N$) ID. Across diverse auction settings, the proposed AMID method substantially increases revenue over first-price formats and outperforms existing benchmark methods.

Learning to Steer Markovian Agents under Model Uncertainty

Designing incentives for an adapting population is a ubiquitous problem in a wide array of economic applications and beyond. In this work, we study how to design additional rewards to steer multi-agent systems towards desired policies \emph{without} prior knowledge of the agents' underlying learning dynamics. We introduce a model-based non-episodic Reinforcement Learning (RL) formulation for our steering problem. Importantly, we focus on learning a \emph{history-dependent} steering strategy to handle the inherent model uncertainty about the agents' learning dynamics. We introduce a novel objective function to encode the desiderata of achieving a good steering outcome with reasonable cost. Theoretically, we identify conditions for the existence of steering strategies to guide agents to the desired policies. Complementing our theoretical contributions, we provide empirical algorithms to approximately solve our objective, which effectively tackles the challenge in learning history-dependent strategies. We demonstrate the efficacy of our algorithms through empirical evaluations.

Stochastic Bilevel Optimization with Lower-Level Contextual Markov Decision Processes

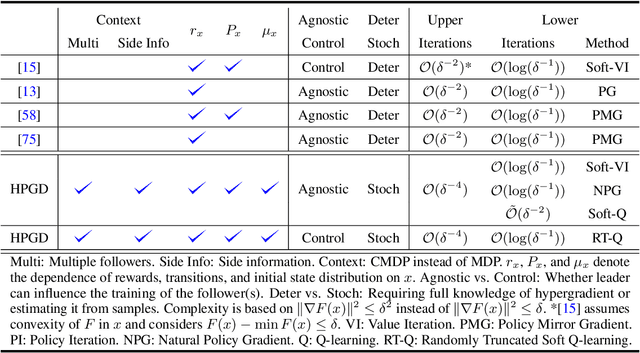
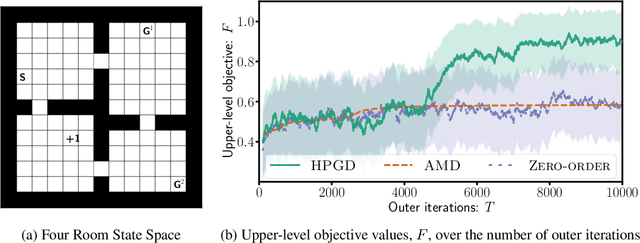
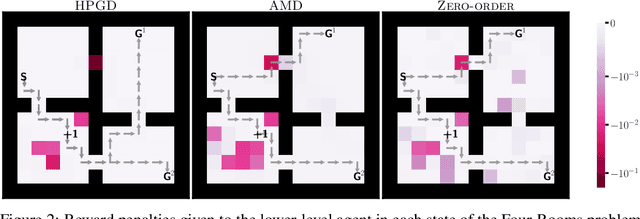
In various applications, the optimal policy in a strategic decision-making problem depends both on the environmental configuration and exogenous events. For these settings, we introduce Bilevel Optimization with Contextual Markov Decision Processes (BO-CMDP), a stochastic bilevel decision-making model, where the lower level consists of solving a contextual Markov Decision Process (CMDP). BO-CMDP can be viewed as a Stackelberg Game where the leader and a random context beyond the leader's control together decide the setup of (many) MDPs that (potentially multiple) followers best respond to. This framework extends beyond traditional bilevel optimization and finds relevance in diverse fields such as model design for MDPs, tax design, reward shaping and dynamic mechanism design. We propose a stochastic Hyper Policy Gradient Descent (HPGD) algorithm to solve BO-CMDP, and demonstrate its convergence. Notably, HPGD only utilizes observations of the followers' trajectories. Therefore, it allows followers to use any training procedure and the leader to be agnostic of the specific algorithm used, which aligns with various real-world scenarios. We further consider the setting when the leader can influence the training of followers and propose an accelerated algorithm. We empirically demonstrate the performance of our algorithm.