Can RLHF be More Efficient with Imperfect Reward Models? A Policy Coverage Perspective

Sample efficiency is critical for online Reinforcement Learning from Human Feedback (RLHF). While existing works investigate sample-efficient online exploration strategies, the potential of utilizing misspecified yet relevant reward models to accelerate learning remains underexplored. This paper studies how to transfer knowledge from those imperfect reward models in online RLHF. We start by identifying a novel property of the KL-regularized RLHF objective: \emph{a policy's ability to cover the optimal policy is captured by its sub-optimality}. Building on this insight, we propose a theoretical transfer learning algorithm with provable benefits compared to standard online learning. Our approach achieves low regret in the early stage by quickly adapting to the best available source reward models without prior knowledge of their quality, and over time, it attains an $\tilde{O}(\sqrt{T})$ regret bound \emph{independent} of structural complexity measures. Inspired by our theoretical findings, we develop an empirical algorithm with improved computational efficiency, and demonstrate its effectiveness empirically in summarization tasks.

Poincaré Inequality for Local Log-Polyak-Lojasiewicz Measures : Non-asymptotic Analysis in Low-temperature Regime

Potential functions in highly pertinent applications, such as deep learning in over-parameterized regime, are empirically observed to admit non-isolated minima. To understand the convergence behavior of stochastic dynamics in such landscapes, we propose to study the class of \logPLmeasure\ measures $\mu_\epsilon \propto \exp(-V/\epsilon)$, where the potential $V$ satisfies a local Polyak-{\L}ojasiewicz (P\L) inequality, and its set of local minima is provably \emph{connected}. Notably, potentials in this class can exhibit local maxima and we characterize its optimal set S to be a compact $\mathcal{C}^2$ \emph{embedding submanifold} of $\mathbb{R}^d$ without boundary. The \emph{non-contractibility} of S distinguishes our function class from the classical convex setting topologically. Moreover, the embedding structure induces a naturally defined Laplacian-Beltrami operator on S, and we show that its first non-trivial eigenvalue provides an \emph{$\epsilon$-independent} lower bound for the \Poincare\ constant in the \Poincare\ inequality of $\mu_\epsilon$. As a direct consequence, Langevin dynamics with such non-convex potential $V$ and diffusion coefficient $\epsilon$ converges to its equilibrium $\mu_\epsilon$ at a rate of $\tilde{\mathcal{O}}(1/\epsilon)$, provided $\epsilon$ is sufficiently small. Here $\tilde{\mathcal{O}}$ hides logarithmic terms.

On the Crucial Role of Initialization for Matrix Factorization

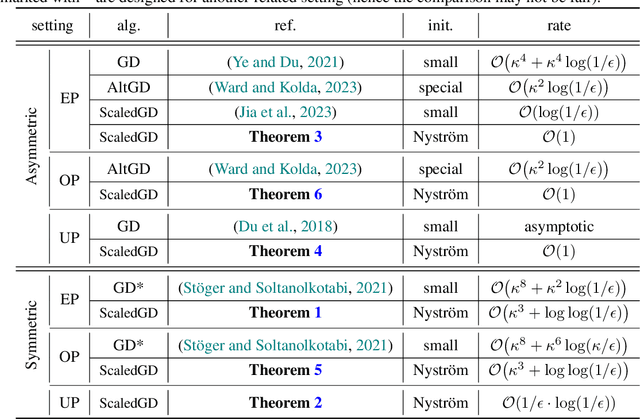
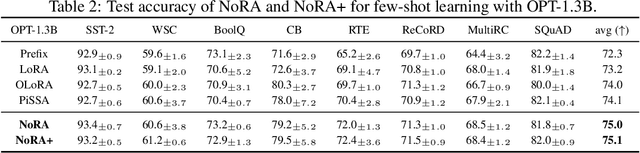
This work revisits the classical low-rank matrix factorization problem and unveils the critical role of initialization in shaping convergence rates for such nonconvex and nonsmooth optimization. We introduce Nystrom initialization, which significantly improves the global convergence of Scaled Gradient Descent (ScaledGD) in both symmetric and asymmetric matrix factorization tasks. Specifically, we prove that ScaledGD with Nystrom initialization achieves quadratic convergence in cases where only linear rates were previously known. Furthermore, we extend this initialization to low-rank adapters (LoRA) commonly used for finetuning foundation models. Our approach, NoRA, i.e., LoRA with Nystrom initialization, demonstrates superior performance across various downstream tasks and model scales, from 1B to 7B parameters, in large language and diffusion models.

Implicit Regularization of Sharpness-Aware Minimization for Scale-Invariant Problems

Sharpness-aware minimization (SAM) improves generalization of various deep learning tasks. Motivated by popular architectures such as LoRA, we explore the implicit regularization of SAM for scale-invariant problems involving two groups of variables. Instead of focusing on commonly used sharpness, this work introduces a concept termed balancedness, defined as the difference between the squared norm of two variables. This allows us to depict richer global behaviors of SAM. In particular, our theoretical and empirical findings reveal that i) SAM promotes balancedness; and ii) the regularization on balancedness is data-responsive -- outliers have stronger impact. The latter coincides with empirical observations that SAM outperforms SGD in the presence of outliers. Leveraging the implicit regularization, we develop a resource-efficient SAM variant, balancedness-aware regularization (BAR), tailored for scale-invariant problems such as finetuning language models with LoRA. BAR saves 95% computational overhead of SAM, with enhanced test performance across various tasks on RoBERTa, GPT2, and OPT-1.3B.

From Gradient Clipping to Normalization for Heavy Tailed SGD

Recent empirical evidence indicates that many machine learning applications involve heavy-tailed gradient noise, which challenges the standard assumptions of bounded variance in stochastic optimization. Gradient clipping has emerged as a popular tool to handle this heavy-tailed noise, as it achieves good performance in this setting both theoretically and practically. However, our current theoretical understanding of non-convex gradient clipping has three main shortcomings. First, the theory hinges on large, increasing clipping thresholds, which are in stark contrast to the small constant clipping thresholds employed in practice. Second, clipping thresholds require knowledge of problem-dependent parameters to guarantee convergence. Lastly, even with this knowledge, current sampling complexity upper bounds for the method are sub-optimal in nearly all parameters. To address these issues, we study convergence of Normalized SGD (NSGD). First, we establish a parameter-free sample complexity for NSGD of $\mathcal{O}\left(\varepsilon^{-\frac{2p}{p-1}}\right)$ to find an $\varepsilon$-stationary point. Furthermore, we prove tightness of this result, by providing a matching algorithm-specific lower bound. In the setting where all problem parameters are known, we show this complexity is improved to $\mathcal{O}\left(\varepsilon^{-\frac{3p-2}{p-1}}\right)$, matching the previously known lower bound for all first-order methods in all problem dependent parameters. Finally, we establish high-probability convergence of NSGD with a mild logarithmic dependence on the failure probability. Our work complements the studies of gradient clipping under heavy tailed noise improving the sample complexities of existing algorithms and offering an alternative mechanism to achieve high probability convergence.

Exploiting Approximate Symmetry for Efficient Multi-Agent Reinforcement Learning

Mean-field games (MFG) have become significant tools for solving large-scale multi-agent reinforcement learning problems under symmetry. However, the assumption of exact symmetry limits the applicability of MFGs, as real-world scenarios often feature inherent heterogeneity. Furthermore, most works on MFG assume access to a known MFG model, which might not be readily available for real-world finite-agent games. In this work, we broaden the applicability of MFGs by providing a methodology to extend any finite-player, possibly asymmetric, game to an "induced MFG". First, we prove that $N$-player dynamic games can be symmetrized and smoothly extended to the infinite-player continuum via explicit Kirszbraun extensions. Next, we propose the notion of $\alpha,\beta$-symmetric games, a new class of dynamic population games that incorporate approximate permutation invariance. For $\alpha,\beta$-symmetric games, we establish explicit approximation bounds, demonstrating that a Nash policy of the induced MFG is an approximate Nash of the $N$-player dynamic game. We show that TD learning converges up to a small bias using trajectories of the $N$-player game with finite-sample guarantees, permitting symmetrized learning without building an explicit MFG model. Finally, for certain games satisfying monotonicity, we prove a sample complexity of $\widetilde{\mathcal{O}}(\varepsilon^{-6})$ for the $N$-agent game to learn an $\varepsilon$-Nash up to symmetrization bias. Our theory is supported by evaluations on MARL benchmarks with thousands of agents.

Multi-level Monte-Carlo Gradient Methods for Stochastic Optimization with Biased Oracles

We consider stochastic optimization when one only has access to biased stochastic oracles of the objective and the gradient, and obtaining stochastic gradients with low biases comes at high costs. This setting captures various optimization paradigms, such as conditional stochastic optimization, distributionally robust optimization, shortfall risk optimization, and machine learning paradigms, such as contrastive learning. We examine a family of multi-level Monte Carlo (MLMC) gradient methods that exploit a delicate tradeoff among bias, variance, and oracle cost. We systematically study their total sample and computational complexities for strongly convex, convex, and nonconvex objectives and demonstrate their superiority over the widely used biased stochastic gradient method. When combined with the variance reduction techniques like SPIDER, these MLMC gradient methods can further reduce the complexity in the nonconvex regime. Our results imply that a series of stochastic optimization problems with biased oracles, previously considered to be more challenging, is fundamentally no harder than the classical stochastic optimization with unbiased oracles. We also delineate the boundary conditions under which these problems become more difficult. Moreover, MLMC gradient methods significantly improve the best-known complexities in the literature for conditional stochastic optimization and shortfall risk optimization. Our extensive numerical experiments on distributionally robust optimization, pricing and staffing scheduling problems, and contrastive learning demonstrate the superior performance of MLMC gradient methods.

Independent Policy Mirror Descent for Markov Potential Games: Scaling to Large Number of Players

Markov Potential Games (MPGs) form an important sub-class of Markov games, which are a common framework to model multi-agent reinforcement learning problems. In particular, MPGs include as a special case the identical-interest setting where all the agents share the same reward function. Scaling the performance of Nash equilibrium learning algorithms to a large number of agents is crucial for multi-agent systems. To address this important challenge, we focus on the independent learning setting where agents can only have access to their local information to update their own policy. In prior work on MPGs, the iteration complexity for obtaining $\epsilon$-Nash regret scales linearly with the number of agents $N$. In this work, we investigate the iteration complexity of an independent policy mirror descent (PMD) algorithm for MPGs. We show that PMD with KL regularization, also known as natural policy gradient, enjoys a better $\sqrt{N}$ dependence on the number of agents, improving over PMD with Euclidean regularization and prior work. Furthermore, the iteration complexity is also independent of the sizes of the agents' action spaces.

Complexity of Minimizing Projected-Gradient-Dominated Functions with Stochastic First-order Oracles

This work investigates the performance limits of projected stochastic first-order methods for minimizing functions under the $(\alpha,\tau,\mathcal{X})$-projected-gradient-dominance property, that asserts the sub-optimality gap $F(\mathbf{x})-\min_{\mathbf{x}'\in \mathcal{X}}F(\mathbf{x}')$ is upper-bounded by $\tau\cdot\|\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})\|^{\alpha}$ for some $\alpha\in[1,2)$ and $\tau>0$ and $\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})$ is the projected-gradient mapping with $\eta>0$ as a parameter. For non-convex functions, we show that the complexity lower bound of querying a batch smooth first-order stochastic oracle to obtain an $\epsilon$-global-optimum point is $\Omega(\epsilon^{-{2}/{\alpha}})$. Furthermore, we show that a projected variance-reduced first-order algorithm can obtain the upper complexity bound of $\mathcal{O}(\epsilon^{-{2}/{\alpha}})$, matching the lower bound. For convex functions, we establish a complexity lower bound of $\Omega(\log(1/\epsilon)\cdot\epsilon^{-{2}/{\alpha}})$ for minimizing functions under a local version of gradient-dominance property, which also matches the upper complexity bound of accelerated stochastic subgradient methods.

Learning to Steer Markovian Agents under Model Uncertainty

Designing incentives for an adapting population is a ubiquitous problem in a wide array of economic applications and beyond. In this work, we study how to design additional rewards to steer multi-agent systems towards desired policies \emph{without} prior knowledge of the agents' underlying learning dynamics. We introduce a model-based non-episodic Reinforcement Learning (RL) formulation for our steering problem. Importantly, we focus on learning a \emph{history-dependent} steering strategy to handle the inherent model uncertainty about the agents' learning dynamics. We introduce a novel objective function to encode the desiderata of achieving a good steering outcome with reasonable cost. Theoretically, we identify conditions for the existence of steering strategies to guide agents to the desired policies. Complementing our theoretical contributions, we provide empirical algorithms to approximately solve our objective, which effectively tackles the challenge in learning history-dependent strategies. We demonstrate the efficacy of our algorithms through empirical evaluations.