From Gradient Clipping to Normalization for Heavy Tailed SGD

Recent empirical evidence indicates that many machine learning applications involve heavy-tailed gradient noise, which challenges the standard assumptions of bounded variance in stochastic optimization. Gradient clipping has emerged as a popular tool to handle this heavy-tailed noise, as it achieves good performance in this setting both theoretically and practically. However, our current theoretical understanding of non-convex gradient clipping has three main shortcomings. First, the theory hinges on large, increasing clipping thresholds, which are in stark contrast to the small constant clipping thresholds employed in practice. Second, clipping thresholds require knowledge of problem-dependent parameters to guarantee convergence. Lastly, even with this knowledge, current sampling complexity upper bounds for the method are sub-optimal in nearly all parameters. To address these issues, we study convergence of Normalized SGD (NSGD). First, we establish a parameter-free sample complexity for NSGD of $\mathcal{O}\left(\varepsilon^{-\frac{2p}{p-1}}\right)$ to find an $\varepsilon$-stationary point. Furthermore, we prove tightness of this result, by providing a matching algorithm-specific lower bound. In the setting where all problem parameters are known, we show this complexity is improved to $\mathcal{O}\left(\varepsilon^{-\frac{3p-2}{p-1}}\right)$, matching the previously known lower bound for all first-order methods in all problem dependent parameters. Finally, we establish high-probability convergence of NSGD with a mild logarithmic dependence on the failure probability. Our work complements the studies of gradient clipping under heavy tailed noise improving the sample complexities of existing algorithms and offering an alternative mechanism to achieve high probability convergence.

Taming Nonconvex Stochastic Mirror Descent with General Bregman Divergence

This paper revisits the convergence of Stochastic Mirror Descent (SMD) in the contemporary nonconvex optimization setting. Existing results for batch-free nonconvex SMD restrict the choice of the distance generating function (DGF) to be differentiable with Lipschitz continuous gradients, thereby excluding important setups such as Shannon entropy. In this work, we present a new convergence analysis of nonconvex SMD supporting general DGF, that overcomes the above limitations and relies solely on the standard assumptions. Moreover, our convergence is established with respect to the Bregman Forward-Backward envelope, which is a stronger measure than the commonly used squared norm of gradient mapping. We further extend our results to guarantee high probability convergence under sub-Gaussian noise and global convergence under the generalized Bregman Proximal Polyak-{\L}ojasiewicz condition. Additionally, we illustrate the advantages of our improved SMD theory in various nonconvex machine learning tasks by harnessing nonsmooth DGFs. Notably, in the context of nonconvex differentially private (DP) learning, our theory yields a simple algorithm with a (nearly) dimension-independent utility bound. For the problem of training linear neural networks, we develop provably convergent stochastic algorithms.

Learning Zero-Sum Linear Quadratic Games with Improved Sample Complexity

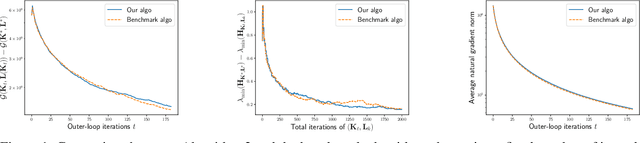
Zero-sum Linear Quadratic (LQ) games are fundamental in optimal control and can be used (i) as a dynamic game formulation for risk-sensitive or robust control, or (ii) as a benchmark setting for multi-agent reinforcement learning with two competing agents in continuous state-control spaces. In contrast to the well-studied single-agent linear quadratic regulator problem, zero-sum LQ games entail solving a challenging nonconvex-nonconcave min-max problem with an objective function that lacks coercivity. Recently, Zhang et al. discovered an implicit regularization property of natural policy gradient methods which is crucial for safety-critical control systems since it preserves the robustness of the controller during learning. Moreover, in the model-free setting where the knowledge of model parameters is not available, Zhang et al. proposed the first polynomial sample complexity algorithm to reach an $\epsilon$-neighborhood of the Nash equilibrium while maintaining the desirable implicit regularization property. In this work, we propose a simpler nested Zeroth-Order (ZO) algorithm improving sample complexity by several orders of magnitude. Our main result guarantees a $\widetilde{\mathcal{O}}(\epsilon^{-3})$ sample complexity under the same assumptions using a single-point ZO estimator. Furthermore, when the estimator is replaced by a two-point estimator, our method enjoys a better $\widetilde{\mathcal{O}}(\epsilon^{-2})$ sample complexity. Our key improvements rely on a more sample-efficient nested algorithm design and finer control of the ZO natural gradient estimation error.

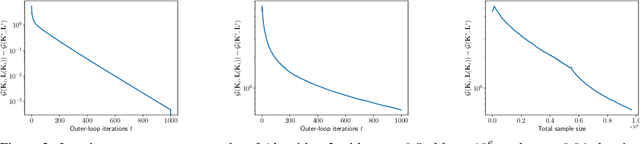
Reinforcement Learning with General Utilities: Simpler Variance Reduction and Large State-Action Space

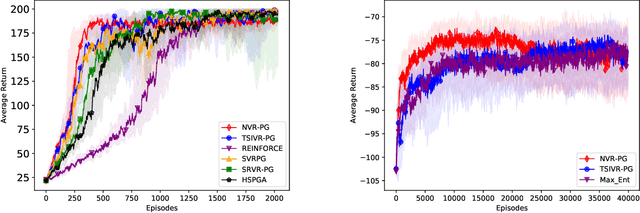
We consider the reinforcement learning (RL) problem with general utilities which consists in maximizing a function of the state-action occupancy measure. Beyond the standard cumulative reward RL setting, this problem includes as particular cases constrained RL, pure exploration and learning from demonstrations among others. For this problem, we propose a simpler single-loop parameter-free normalized policy gradient algorithm. Implementing a recursive momentum variance reduction mechanism, our algorithm achieves $\tilde{\mathcal{O}}(\epsilon^{-3})$ and $\tilde{\mathcal{O}}(\epsilon^{-2})$ sample complexities for $\epsilon$-first-order stationarity and $\epsilon$-global optimality respectively, under adequate assumptions. We further address the setting of large finite state action spaces via linear function approximation of the occupancy measure and show a $\tilde{\mathcal{O}}(\epsilon^{-4})$ sample complexity for a simple policy gradient method with a linear regression subroutine.

Momentum Provably Improves Error Feedback!

Due to the high communication overhead when training machine learning models in a distributed environment, modern algorithms invariably rely on lossy communication compression. However, when untreated, the errors caused by compression propagate, and can lead to severely unstable behavior, including exponential divergence. Almost a decade ago, Seide et al [2014] proposed an error feedback (EF) mechanism, which we refer to as EF14, as an immensely effective heuristic for mitigating this issue. However, despite steady algorithmic and theoretical advances in the EF field in the last decade, our understanding is far from complete. In this work we address one of the most pressing issues. In particular, in the canonical nonconvex setting, all known variants of EF rely on very large batch sizes to converge, which can be prohibitive in practice. We propose a surprisingly simple fix which removes this issue both theoretically, and in practice: the application of Polyak's momentum to the latest incarnation of EF due to Richt\'{a}rik et al. [2021] known as EF21. Our algorithm, for which we coin the name EF21-SGDM, improves the communication and sample complexities of previous error feedback algorithms under standard smoothness and bounded variance assumptions, and does not require any further strong assumptions such as bounded gradient dissimilarity. Moreover, we propose a double momentum version of our method that improves the complexities even further. Our proof seems to be novel even when compression is removed from the method, and as such, our proof technique is of independent interest in the study of nonconvex stochastic optimization enriched with Polyak's momentum.

Two Sides of One Coin: the Limits of Untuned SGD and the Power of Adaptive Methods

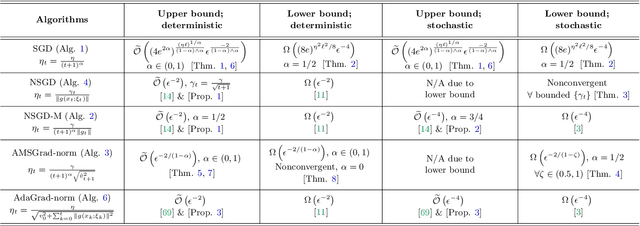
The classical analysis of Stochastic Gradient Descent (SGD) with polynomially decaying stepsize $\eta_t = \eta/\sqrt{t}$ relies on well-tuned $\eta$ depending on problem parameters such as Lipschitz smoothness constant, which is often unknown in practice. In this work, we prove that SGD with arbitrary $\eta > 0$, referred to as untuned SGD, still attains an order-optimal convergence rate $\widetilde{O}(T^{-1/4})$ in terms of gradient norm for minimizing smooth objectives. Unfortunately, it comes at the expense of a catastrophic exponential dependence on the smoothness constant, which we show is unavoidable for this scheme even in the noiseless setting. We then examine three families of adaptive methods $\unicode{x2013}$ Normalized SGD (NSGD), AMSGrad, and AdaGrad $\unicode{x2013}$ unveiling their power in preventing such exponential dependency in the absence of information about the smoothness parameter and boundedness of stochastic gradients. Our results provide theoretical justification for the advantage of adaptive methods over untuned SGD in alleviating the issue with large gradients.

Stochastic Policy Gradient Methods: Improved Sample Complexity for Fisher-non-degenerate Policies

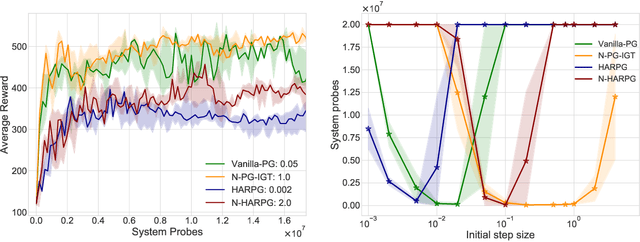
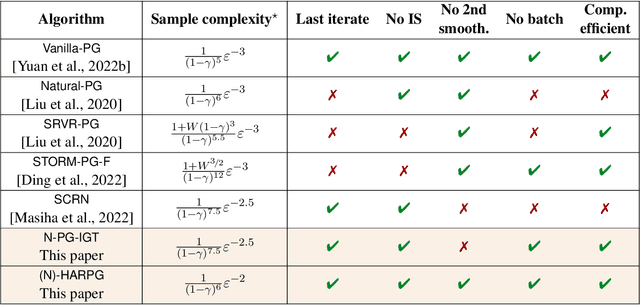
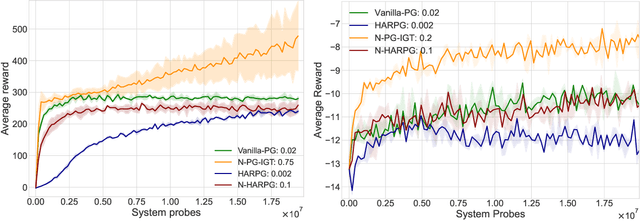
Recently, the impressive empirical success of policy gradient (PG) methods has catalyzed the development of their theoretical foundations. Despite the huge efforts directed at the design of efficient stochastic PG-type algorithms, the understanding of their convergence to a globally optimal policy is still limited. In this work, we develop improved global convergence guarantees for a general class of Fisher-non-degenerate parameterized policies which allows to address the case of continuous state action spaces. First, we propose a Normalized Policy Gradient method with Implicit Gradient Transport (N-PG-IGT) and derive a $\tilde{\mathcal{O}}(\varepsilon^{-2.5})$ sample complexity of this method for finding a global $\varepsilon$-optimal policy. Improving over the previously known $\tilde{\mathcal{O}}(\varepsilon^{-3})$ complexity, this algorithm does not require the use of importance sampling or second-order information and samples only one trajectory per iteration. Second, we further improve this complexity to $\tilde{ \mathcal{\mathcal{O}} }(\varepsilon^{-2})$ by considering a Hessian-Aided Recursive Policy Gradient ((N)-HARPG) algorithm enhanced with a correction based on a Hessian-vector product. Interestingly, both algorithms are $(i)$ simple and easy to implement: single-loop, do not require large batches of trajectories and sample at most two trajectories per iteration; $(ii)$ computationally and memory efficient: they do not require expensive subroutines at each iteration and can be implemented with memory linear in the dimension of parameters.

3PC: Three Point Compressors for Communication-Efficient Distributed Training and a Better Theory for Lazy Aggregation

We propose and study a new class of gradient communication mechanisms for communication-efficient training -- three point compressors (3PC) -- as well as efficient distributed nonconvex optimization algorithms that can take advantage of them. Unlike most established approaches, which rely on a static compressor choice (e.g., Top-$K$), our class allows the compressors to {\em evolve} throughout the training process, with the aim of improving the theoretical communication complexity and practical efficiency of the underlying methods. We show that our general approach can recover the recently proposed state-of-the-art error feedback mechanism EF21 (Richt\'arik et al., 2021) and its theoretical properties as a special case, but also leads to a number of new efficient methods. Notably, our approach allows us to improve upon the state of the art in the algorithmic and theoretical foundations of the {\em lazy aggregation} literature (Chen et al., 2018). As a by-product that may be of independent interest, we provide a new and fundamental link between the lazy aggregation and error feedback literature. A special feature of our work is that we do not require the compressors to be unbiased.

EF21 with Bells & Whistles: Practical Algorithmic Extensions of Modern Error Feedback

First proposed by Seide (2014) as a heuristic, error feedback (EF) is a very popular mechanism for enforcing convergence of distributed gradient-based optimization methods enhanced with communication compression strategies based on the application of contractive compression operators. However, existing theory of EF relies on very strong assumptions (e.g., bounded gradients), and provides pessimistic convergence rates (e.g., while the best known rate for EF in the smooth nonconvex regime, and when full gradients are compressed, is $O(1/T^{2/3})$, the rate of gradient descent in the same regime is $O(1/T)$). Recently, Richt\'{a}rik et al. (2021) proposed a new error feedback mechanism, EF21, based on the construction of a Markov compressor induced by a contractive compressor. EF21 removes the aforementioned theoretical deficiencies of EF and at the same time works better in practice. In this work we propose six practical extensions of EF21, all supported by strong convergence theory: partial participation, stochastic approximation, variance reduction, proximal setting, momentum and bidirectional compression. Several of these techniques were never analyzed in conjunction with EF before, and in cases where they were (e.g., bidirectional compression), our rates are vastly superior.

EF21: A New, Simpler, Theoretically Better, and Practically Faster Error Feedback

Error feedback (EF), also known as error compensation, is an immensely popular convergence stabilization mechanism in the context of distributed training of supervised machine learning models enhanced by the use of contractive communication compression mechanisms, such as Top-$k$. First proposed by Seide et al (2014) as a heuristic, EF resisted any theoretical understanding until recently [Stich et al., 2018, Alistarh et al., 2018]. However, all existing analyses either i) apply to the single node setting only, ii) rely on very strong and often unreasonable assumptions, such global boundedness of the gradients, or iterate-dependent assumptions that cannot be checked a-priori and may not hold in practice, or iii) circumvent these issues via the introduction of additional unbiased compressors, which increase the communication cost. In this work we fix all these deficiencies by proposing and analyzing a new EF mechanism, which we call EF21, which consistently and substantially outperforms EF in practice. Our theoretical analysis relies on standard assumptions only, works in the distributed heterogeneous data setting, and leads to better and more meaningful rates. In particular, we prove that EF21 enjoys a fast $O(1/T)$ convergence rate for smooth nonconvex problems, beating the previous bound of $O(1/T^{2/3})$, which was shown a bounded gradients assumption. We further improve this to a fast linear rate for PL functions, which is the first linear convergence result for an EF-type method not relying on unbiased compressors. Since EF has a large number of applications where it reigns supreme, we believe that our 2021 variant, EF21, can a large impact on the practice of communication efficient distributed learning.