Learning Zero-Sum Linear Quadratic Games with Improved Sample Complexity
Paper and Code
Sep 08, 2023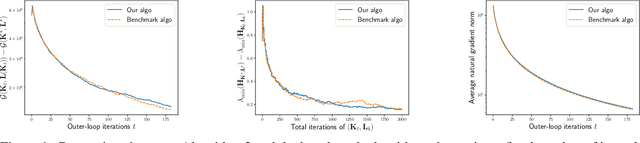
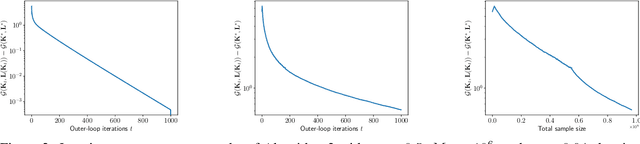
Zero-sum Linear Quadratic (LQ) games are fundamental in optimal control and can be used (i) as a dynamic game formulation for risk-sensitive or robust control, or (ii) as a benchmark setting for multi-agent reinforcement learning with two competing agents in continuous state-control spaces. In contrast to the well-studied single-agent linear quadratic regulator problem, zero-sum LQ games entail solving a challenging nonconvex-nonconcave min-max problem with an objective function that lacks coercivity. Recently, Zhang et al. discovered an implicit regularization property of natural policy gradient methods which is crucial for safety-critical control systems since it preserves the robustness of the controller during learning. Moreover, in the model-free setting where the knowledge of model parameters is not available, Zhang et al. proposed the first polynomial sample complexity algorithm to reach an $\epsilon$-neighborhood of the Nash equilibrium while maintaining the desirable implicit regularization property. In this work, we propose a simpler nested Zeroth-Order (ZO) algorithm improving sample complexity by several orders of magnitude. Our main result guarantees a $\widetilde{\mathcal{O}}(\epsilon^{-3})$ sample complexity under the same assumptions using a single-point ZO estimator. Furthermore, when the estimator is replaced by a two-point estimator, our method enjoys a better $\widetilde{\mathcal{O}}(\epsilon^{-2})$ sample complexity. Our key improvements rely on a more sample-efficient nested algorithm design and finer control of the ZO natural gradient estimation error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge