Multi-Agent Online Control with Adversarial Disturbances

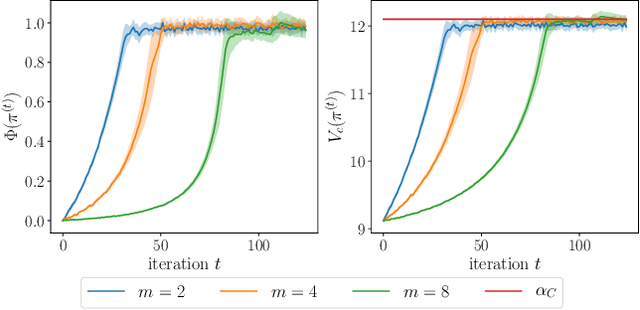
Multi-agent control problems involving a large number of agents with competing and time-varying objectives are increasingly prevalent in applications across robotics, economics, and energy systems. In this paper, we study online control in multi-agent linear dynamical systems with disturbances. In contrast to most prior work in multi-agent control, we consider an online setting where disturbances are adversarial and where each agent seeks to minimize its own, adversarial sequence of convex losses. In this setting, we investigate the robustness of gradient-based controllers from single-agent online control, with a particular focus on understanding how individual regret guarantees are influenced by the number of agents in the system. Under minimal communication assumptions, we prove near-optimal sublinear regret bounds that hold uniformly for all agents. Finally, when the objectives of the agents are aligned, we show that the multi-agent control problem induces a time-varying potential game for which we derive equilibrium gap guarantees.

Optimistic Online Learning in Symmetric Cone Games

Optimistic online learning algorithms have led to significant advances in equilibrium computation, particularly for two-player zero-sum games, achieving an iteration complexity of $\mathcal{O}(1/\epsilon)$ to reach an $\epsilon$-saddle point. These advances have been established in normal-form games, where strategies are simplex vectors, and quantum games, where strategies are trace-one positive semidefinite matrices. We extend optimistic learning to symmetric cone games (SCGs), a class of two-player zero-sum games where strategy spaces are generalized simplices (trace-one slices of symmetric cones). A symmetric cone is the cone of squares of a Euclidean Jordan Algebra; canonical examples include the nonnegative orthant, the second-order cone, the cone of positive semidefinite matrices, and their products, all fundamental to convex optimization. SCGs unify normal-form and quantum games and, as we show, offer significantly greater modeling flexibility, allowing us to model applications such as distance metric learning problems and the Fermat-Weber problem. To compute approximate saddle points in SCGs, we introduce the Optimistic Symmetric Cone Multiplicative Weights Update algorithm and establish an iteration complexity of $\mathcal{O}(1/\epsilon)$ to reach an $\epsilon$-saddle point. Our analysis builds on the Optimistic Follow-the-Regularized-Leader framework, with a key technical contribution being a new proof of the strong convexity of the symmetric cone negative entropy with respect to the trace-one norm, a result that may be of independent interest.

On the Sample Complexity of a Policy Gradient Algorithm with Occupancy Approximation for General Utility Reinforcement Learning

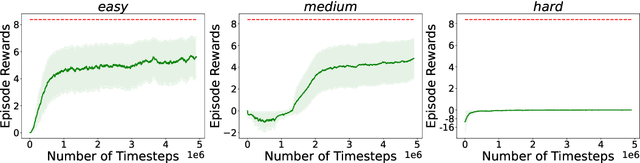
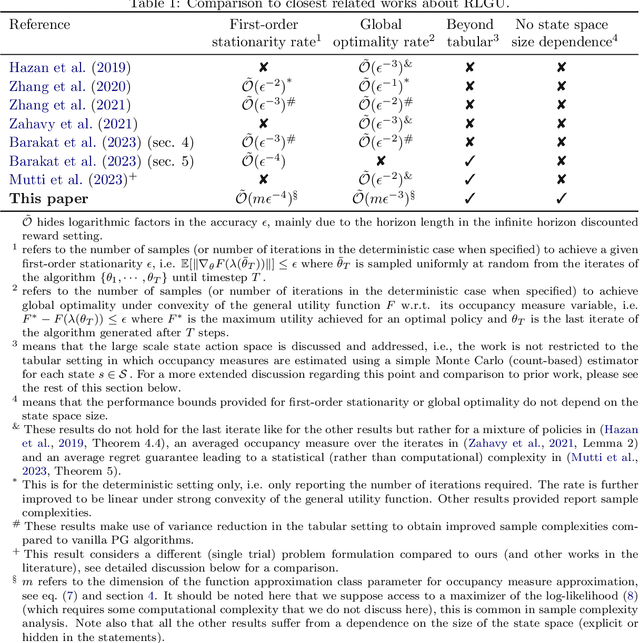
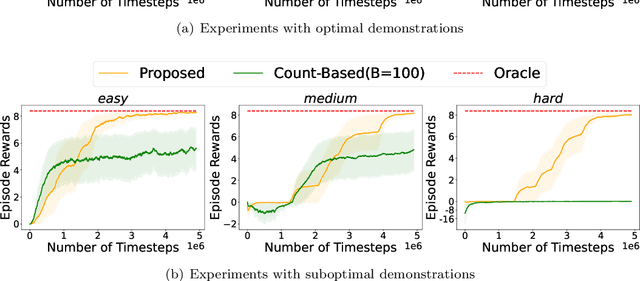
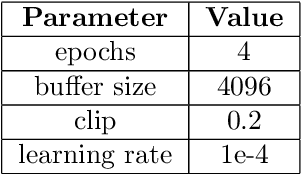
Reinforcement learning with general utilities has recently gained attention thanks to its ability to unify several problems, including imitation learning, pure exploration, and safe RL. However, prior work for solving this general problem in a unified way has mainly focused on the tabular setting. This is restrictive when considering larger state-action spaces because of the need to estimate occupancy measures during policy optimization. In this work, we address this issue and propose to approximate occupancy measures within a function approximation class using maximum likelihood estimation (MLE). We propose a simple policy gradient algorithm (PG-OMA) where an actor updates the policy parameters to maximize the general utility objective whereas a critic approximates the occupancy measure using MLE. We provide a sample complexity analysis of PG-OMA showing that our occupancy measure estimation error only scales with the dimension of our function approximation class rather than the size of the state action space. Under suitable assumptions, we establish first order stationarity and global optimality performance bounds for the proposed PG-OMA algorithm for nonconcave and concave general utilities respectively. We complement our methodological and theoretical findings with promising empirical results showing the scalability potential of our approach compared to existing tabular count-based approaches.

Beyond Expected Returns: A Policy Gradient Algorithm for Cumulative Prospect Theoretic Reinforcement Learning

The widely used expected utility theory has been shown to be empirically inconsistent with human preferences in the psychology and behavioral economy literatures. Cumulative Prospect Theory (CPT) has been developed to fill in this gap and provide a better model for human-based decision-making supported by empirical evidence. It allows to express a wide range of attitudes and perceptions towards risk, gains and losses. A few years ago, CPT has been combined with Reinforcement Learning (RL) to formulate a CPT policy optimization problem where the goal of the agent is to search for a policy generating long-term returns which are aligned with their preferences. In this work, we revisit this policy optimization problem and provide new insights on optimal policies and their nature depending on the utility function under consideration. We further derive a novel policy gradient theorem for the CPT policy optimization objective generalizing the seminal corresponding result in standard RL. This result enables us to design a model-free policy gradient algorithm to solve the CPT-RL problem. We illustrate the performance of our algorithm in simple examples motivated by traffic control and electricity management applications. We also demonstrate that our policy gradient algorithm scales better to larger state spaces compared to the existing zeroth order algorithm for solving the same problem.

Independent Policy Mirror Descent for Markov Potential Games: Scaling to Large Number of Players

Markov Potential Games (MPGs) form an important sub-class of Markov games, which are a common framework to model multi-agent reinforcement learning problems. In particular, MPGs include as a special case the identical-interest setting where all the agents share the same reward function. Scaling the performance of Nash equilibrium learning algorithms to a large number of agents is crucial for multi-agent systems. To address this important challenge, we focus on the independent learning setting where agents can only have access to their local information to update their own policy. In prior work on MPGs, the iteration complexity for obtaining $\epsilon$-Nash regret scales linearly with the number of agents $N$. In this work, we investigate the iteration complexity of an independent policy mirror descent (PMD) algorithm for MPGs. We show that PMD with KL regularization, also known as natural policy gradient, enjoys a better $\sqrt{N}$ dependence on the number of agents, improving over PMD with Euclidean regularization and prior work. Furthermore, the iteration complexity is also independent of the sizes of the agents' action spaces.

Policy Mirror Descent with Lookahead

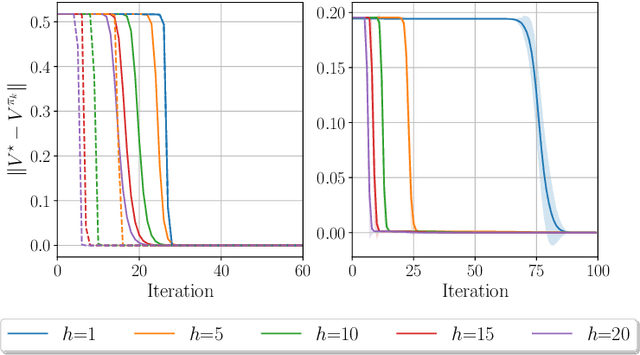
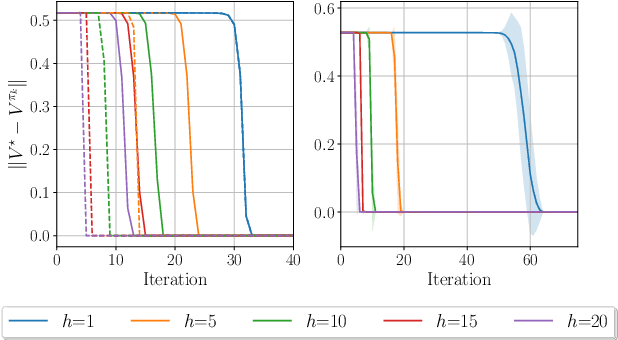
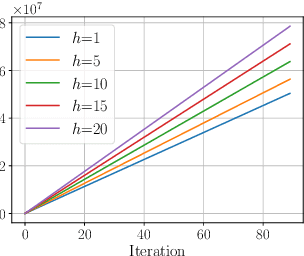
Policy Mirror Descent (PMD) stands as a versatile algorithmic framework encompassing several seminal policy gradient algorithms such as natural policy gradient, with connections with state-of-the-art reinforcement learning (RL) algorithms such as TRPO and PPO. PMD can be seen as a soft Policy Iteration algorithm implementing regularized 1-step greedy policy improvement. However, 1-step greedy policies might not be the best choice and recent remarkable empirical successes in RL such as AlphaGo and AlphaZero have demonstrated that greedy approaches with respect to multiple steps outperform their 1-step counterpart. In this work, we propose a new class of PMD algorithms called $h$-PMD which incorporates multi-step greedy policy improvement with lookahead depth $h$ to the PMD update rule. To solve discounted infinite horizon Markov Decision Processes with discount factor $\gamma$, we show that $h$-PMD which generalizes the standard PMD enjoys a faster dimension-free $\gamma^h$-linear convergence rate, contingent on the computation of multi-step greedy policies. We propose an inexact version of $h$-PMD where lookahead action values are estimated. Under a generative model, we establish a sample complexity for $h$-PMD which improves over prior work. Finally, we extend our result to linear function approximation to scale to large state spaces. Under suitable assumptions, our sample complexity only involves dependence on the dimension of the feature map space instead of the state space size.

Independent Learning in Constrained Markov Potential Games

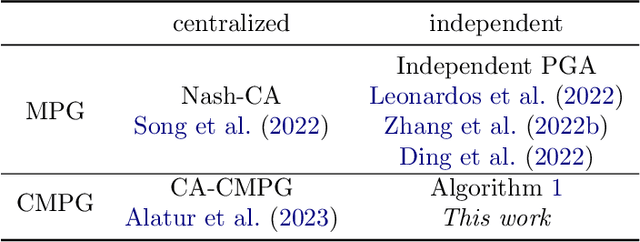
Constrained Markov games offer a formal mathematical framework for modeling multi-agent reinforcement learning problems where the behavior of the agents is subject to constraints. In this work, we focus on the recently introduced class of constrained Markov Potential Games. While centralized algorithms have been proposed for solving such constrained games, the design of converging independent learning algorithms tailored for the constrained setting remains an open question. We propose an independent policy gradient algorithm for learning approximate constrained Nash equilibria: Each agent observes their own actions and rewards, along with a shared state. Inspired by the optimization literature, our algorithm performs proximal-point-like updates augmented with a regularized constraint set. Each proximal step is solved inexactly using a stochastic switching gradient algorithm. Notably, our algorithm can be implemented independently without a centralized coordination mechanism requiring turn-based agent updates. Under some technical constraint qualification conditions, we establish convergence guarantees towards constrained approximate Nash equilibria. We perform simulations to illustrate our results.

Learning Zero-Sum Linear Quadratic Games with Improved Sample Complexity

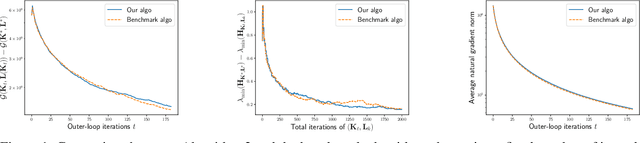
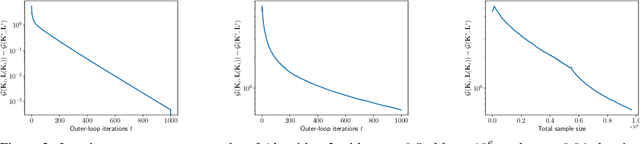
Zero-sum Linear Quadratic (LQ) games are fundamental in optimal control and can be used (i) as a dynamic game formulation for risk-sensitive or robust control, or (ii) as a benchmark setting for multi-agent reinforcement learning with two competing agents in continuous state-control spaces. In contrast to the well-studied single-agent linear quadratic regulator problem, zero-sum LQ games entail solving a challenging nonconvex-nonconcave min-max problem with an objective function that lacks coercivity. Recently, Zhang et al. discovered an implicit regularization property of natural policy gradient methods which is crucial for safety-critical control systems since it preserves the robustness of the controller during learning. Moreover, in the model-free setting where the knowledge of model parameters is not available, Zhang et al. proposed the first polynomial sample complexity algorithm to reach an $\epsilon$-neighborhood of the Nash equilibrium while maintaining the desirable implicit regularization property. In this work, we propose a simpler nested Zeroth-Order (ZO) algorithm improving sample complexity by several orders of magnitude. Our main result guarantees a $\widetilde{\mathcal{O}}(\epsilon^{-3})$ sample complexity under the same assumptions using a single-point ZO estimator. Furthermore, when the estimator is replaced by a two-point estimator, our method enjoys a better $\widetilde{\mathcal{O}}(\epsilon^{-2})$ sample complexity. Our key improvements rely on a more sample-efficient nested algorithm design and finer control of the ZO natural gradient estimation error.

Reinforcement Learning with General Utilities: Simpler Variance Reduction and Large State-Action Space

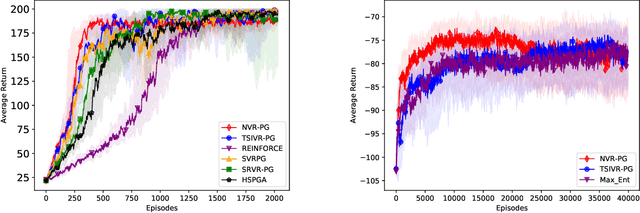
We consider the reinforcement learning (RL) problem with general utilities which consists in maximizing a function of the state-action occupancy measure. Beyond the standard cumulative reward RL setting, this problem includes as particular cases constrained RL, pure exploration and learning from demonstrations among others. For this problem, we propose a simpler single-loop parameter-free normalized policy gradient algorithm. Implementing a recursive momentum variance reduction mechanism, our algorithm achieves $\tilde{\mathcal{O}}(\epsilon^{-3})$ and $\tilde{\mathcal{O}}(\epsilon^{-2})$ sample complexities for $\epsilon$-first-order stationarity and $\epsilon$-global optimality respectively, under adequate assumptions. We further address the setting of large finite state action spaces via linear function approximation of the occupancy measure and show a $\tilde{\mathcal{O}}(\epsilon^{-4})$ sample complexity for a simple policy gradient method with a linear regression subroutine.

Stochastic Policy Gradient Methods: Improved Sample Complexity for Fisher-non-degenerate Policies

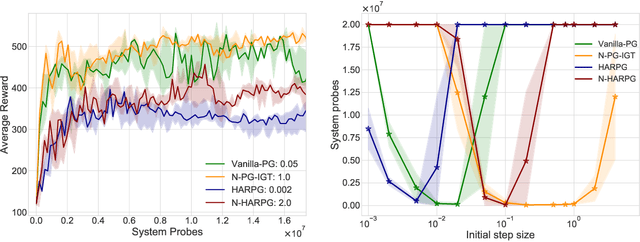
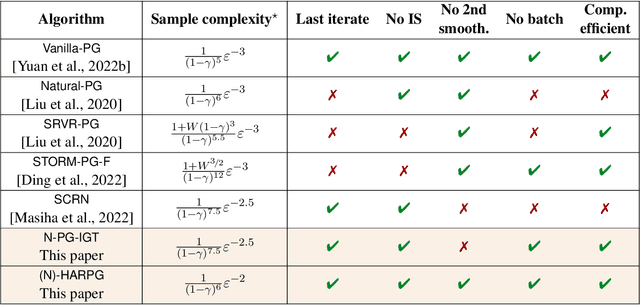
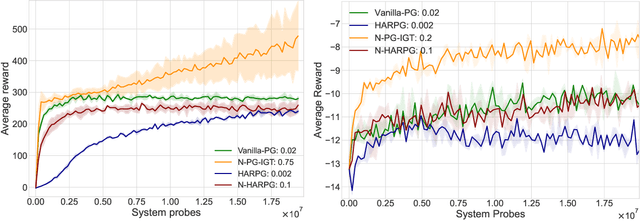
Recently, the impressive empirical success of policy gradient (PG) methods has catalyzed the development of their theoretical foundations. Despite the huge efforts directed at the design of efficient stochastic PG-type algorithms, the understanding of their convergence to a globally optimal policy is still limited. In this work, we develop improved global convergence guarantees for a general class of Fisher-non-degenerate parameterized policies which allows to address the case of continuous state action spaces. First, we propose a Normalized Policy Gradient method with Implicit Gradient Transport (N-PG-IGT) and derive a $\tilde{\mathcal{O}}(\varepsilon^{-2.5})$ sample complexity of this method for finding a global $\varepsilon$-optimal policy. Improving over the previously known $\tilde{\mathcal{O}}(\varepsilon^{-3})$ complexity, this algorithm does not require the use of importance sampling or second-order information and samples only one trajectory per iteration. Second, we further improve this complexity to $\tilde{ \mathcal{\mathcal{O}} }(\varepsilon^{-2})$ by considering a Hessian-Aided Recursive Policy Gradient ((N)-HARPG) algorithm enhanced with a correction based on a Hessian-vector product. Interestingly, both algorithms are $(i)$ simple and easy to implement: single-loop, do not require large batches of trajectories and sample at most two trajectories per iteration; $(ii)$ computationally and memory efficient: they do not require expensive subroutines at each iteration and can be implemented with memory linear in the dimension of parameters.