Reinforcement Learning with General Utilities: Simpler Variance Reduction and Large State-Action Space
Paper and Code
Jun 02, 2023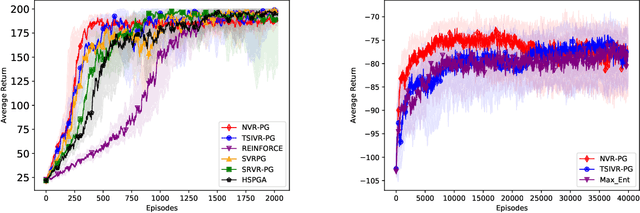
We consider the reinforcement learning (RL) problem with general utilities which consists in maximizing a function of the state-action occupancy measure. Beyond the standard cumulative reward RL setting, this problem includes as particular cases constrained RL, pure exploration and learning from demonstrations among others. For this problem, we propose a simpler single-loop parameter-free normalized policy gradient algorithm. Implementing a recursive momentum variance reduction mechanism, our algorithm achieves $\tilde{\mathcal{O}}(\epsilon^{-3})$ and $\tilde{\mathcal{O}}(\epsilon^{-2})$ sample complexities for $\epsilon$-first-order stationarity and $\epsilon$-global optimality respectively, under adequate assumptions. We further address the setting of large finite state action spaces via linear function approximation of the occupancy measure and show a $\tilde{\mathcal{O}}(\epsilon^{-4})$ sample complexity for a simple policy gradient method with a linear regression subroutine.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge