Nash Equilibria in Games with Playerwise Concave Coupling Constraints: Existence and Computation

We study the existence and computation of Nash equilibria in continuous static games where the players' admissible strategies are subject to shared coupling constraints, i.e., constraints that depend on their \emph{joint} strategies. Specifically, we focus on a class of games characterized by playerwise concave utilities and playerwise concave constraints. Prior results on the existence of Nash equilibria are not applicable to this class, as they rely on strong assumptions such as joint convexity of the feasible set. By leveraging topological fixed point theory and novel structural insights into the contractibility of feasible sets under playerwise concave constraints, we give an existence proof for Nash equilibria under weaker conditions. Having established existence, we then focus on the computation of Nash equilibria via independent gradient methods under the additional assumption that the utilities admit a potential function. To account for the possibly nonconvex feasible region, we employ a log barrier regularized gradient ascent with adaptive stepsizes. Starting from an initial feasible strategy profile and under exact gradient feedback, the proposed method converges to an $\epsilon$-approximate constrained Nash equilibrium within $\mathcal{O}(\epsilon^{-3})$ iterations.

Independent Learning in Constrained Markov Potential Games

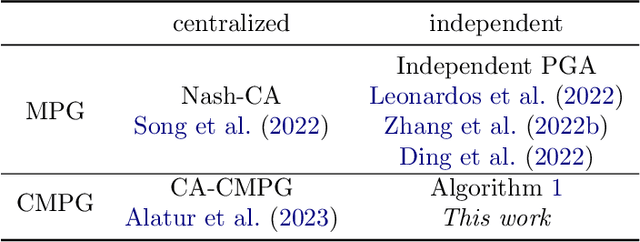
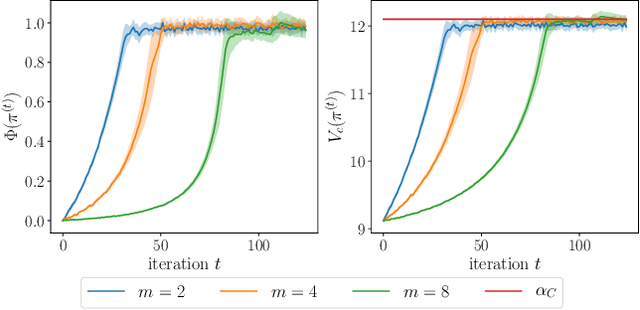
Constrained Markov games offer a formal mathematical framework for modeling multi-agent reinforcement learning problems where the behavior of the agents is subject to constraints. In this work, we focus on the recently introduced class of constrained Markov Potential Games. While centralized algorithms have been proposed for solving such constrained games, the design of converging independent learning algorithms tailored for the constrained setting remains an open question. We propose an independent policy gradient algorithm for learning approximate constrained Nash equilibria: Each agent observes their own actions and rewards, along with a shared state. Inspired by the optimization literature, our algorithm performs proximal-point-like updates augmented with a regularized constraint set. Each proximal step is solved inexactly using a stochastic switching gradient algorithm. Notably, our algorithm can be implemented independently without a centralized coordination mechanism requiring turn-based agent updates. Under some technical constraint qualification conditions, we establish convergence guarantees towards constrained approximate Nash equilibria. We perform simulations to illustrate our results.

Decentralized Federated Policy Gradient with Byzantine Fault-Tolerance and Provably Fast Convergence

In Federated Reinforcement Learning (FRL), agents aim to collaboratively learn a common task, while each agent is acting in its local environment without exchanging raw trajectories. Existing approaches for FRL either (a) do not provide any fault-tolerance guarantees (against misbehaving agents), or (b) rely on a trusted central agent (a single point of failure) for aggregating updates. We provide the first decentralized Byzantine fault-tolerant FRL method. Towards this end, we first propose a new centralized Byzantine fault-tolerant policy gradient (PG) algorithm that improves over existing methods by relying only on assumptions standard for non-fault-tolerant PG. Then, as our main contribution, we show how a combination of robust aggregation and Byzantine-resilient agreement methods can be leveraged in order to eliminate the need for a trusted central entity. Since our results represent the first sample complexity analysis for Byzantine fault-tolerant decentralized federated non-convex optimization, our technical contributions may be of independent interest. Finally, we corroborate our theoretical results experimentally for common RL environments, demonstrating the speed-up of decentralized federations w.r.t. the number of participating agents and resilience against various Byzantine attacks.