Independent Learning in Constrained Markov Potential Games
Paper and Code
Feb 27, 2024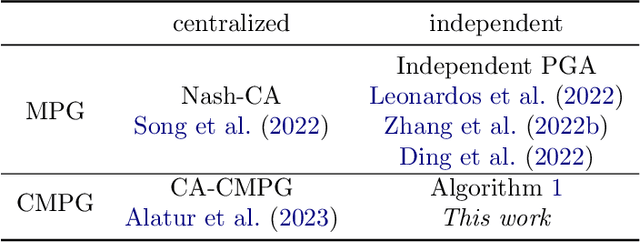
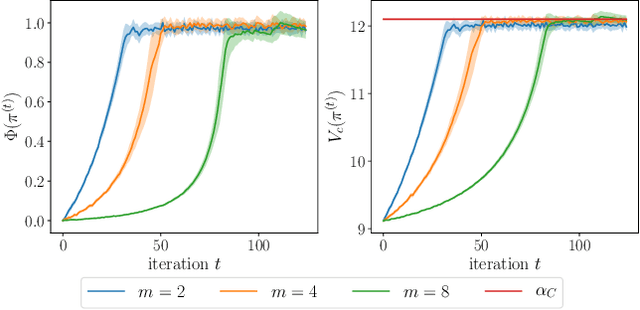
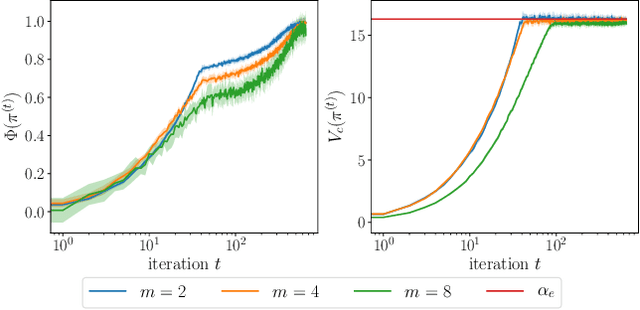
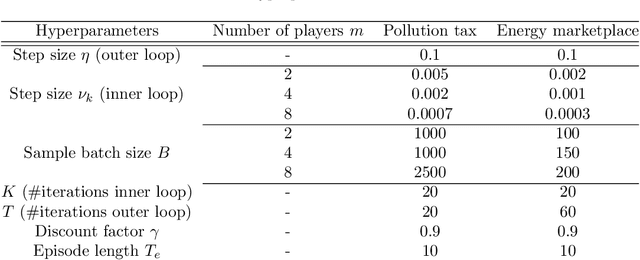
Constrained Markov games offer a formal mathematical framework for modeling multi-agent reinforcement learning problems where the behavior of the agents is subject to constraints. In this work, we focus on the recently introduced class of constrained Markov Potential Games. While centralized algorithms have been proposed for solving such constrained games, the design of converging independent learning algorithms tailored for the constrained setting remains an open question. We propose an independent policy gradient algorithm for learning approximate constrained Nash equilibria: Each agent observes their own actions and rewards, along with a shared state. Inspired by the optimization literature, our algorithm performs proximal-point-like updates augmented with a regularized constraint set. Each proximal step is solved inexactly using a stochastic switching gradient algorithm. Notably, our algorithm can be implemented independently without a centralized coordination mechanism requiring turn-based agent updates. Under some technical constraint qualification conditions, we establish convergence guarantees towards constrained approximate Nash equilibria. We perform simulations to illustrate our results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge