Independent Policy Mirror Descent for Markov Potential Games: Scaling to Large Number of Players

Markov Potential Games (MPGs) form an important sub-class of Markov games, which are a common framework to model multi-agent reinforcement learning problems. In particular, MPGs include as a special case the identical-interest setting where all the agents share the same reward function. Scaling the performance of Nash equilibrium learning algorithms to a large number of agents is crucial for multi-agent systems. To address this important challenge, we focus on the independent learning setting where agents can only have access to their local information to update their own policy. In prior work on MPGs, the iteration complexity for obtaining $\epsilon$-Nash regret scales linearly with the number of agents $N$. In this work, we investigate the iteration complexity of an independent policy mirror descent (PMD) algorithm for MPGs. We show that PMD with KL regularization, also known as natural policy gradient, enjoys a better $\sqrt{N}$ dependence on the number of agents, improving over PMD with Euclidean regularization and prior work. Furthermore, the iteration complexity is also independent of the sizes of the agents' action spaces.

Truly No-Regret Learning in Constrained MDPs

Constrained Markov decision processes (CMDPs) are a common way to model safety constraints in reinforcement learning. State-of-the-art methods for efficiently solving CMDPs are based on primal-dual algorithms. For these algorithms, all currently known regret bounds allow for error cancellations -- one can compensate for a constraint violation in one round with a strict constraint satisfaction in another. This makes the online learning process unsafe since it only guarantees safety for the final (mixture) policy but not during learning. As Efroni et al. (2020) pointed out, it is an open question whether primal-dual algorithms can provably achieve sublinear regret if we do not allow error cancellations. In this paper, we give the first affirmative answer. We first generalize a result on last-iterate convergence of regularized primal-dual schemes to CMDPs with multiple constraints. Building upon this insight, we propose a model-based primal-dual algorithm to learn in an unknown CMDP. We prove that our algorithm achieves sublinear regret without error cancellations.

Provably Learning Nash Policies in Constrained Markov Potential Games

Multi-agent reinforcement learning (MARL) addresses sequential decision-making problems with multiple agents, where each agent optimizes its own objective. In many real-world instances, the agents may not only want to optimize their objectives, but also ensure safe behavior. For example, in traffic routing, each car (agent) aims to reach its destination quickly (objective) while avoiding collisions (safety). Constrained Markov Games (CMGs) are a natural formalism for safe MARL problems, though generally intractable. In this work, we introduce and study Constrained Markov Potential Games (CMPGs), an important class of CMGs. We first show that a Nash policy for CMPGs can be found via constrained optimization. One tempting approach is to solve it by Lagrangian-based primal-dual methods. As we show, in contrast to the single-agent setting, however, CMPGs do not satisfy strong duality, rendering such approaches inapplicable and potentially unsafe. To solve the CMPG problem, we propose our algorithm Coordinate-Ascent for CMPGs (CA-CMPG), which provably converges to a Nash policy in tabular, finite-horizon CMPGs. Furthermore, we provide the first sample complexity bounds for learning Nash policies in unknown CMPGs, and, which under additional assumptions, guarantee safe exploration.

Cancellation-Free Regret Bounds for Lagrangian Approaches in Constrained Markov Decision Processes

Constrained Markov Decision Processes (CMDPs) are one of the common ways to model safe reinforcement learning problems, where the safety objectives are modeled by constraint functions. Lagrangian-based dual or primal-dual algorithms provide efficient methods for learning in CMDPs. For these algorithms, the currently known regret bounds in the finite-horizon setting allow for a \textit{cancellation of errors}; that is, one can compensate for a constraint violation in one episode with a strict constraint satisfaction in another episode. However, in practical applications, we do not consider such a behavior safe. In this paper, we overcome this weakness by proposing a novel model-based dual algorithm \textsc{OptAug-CMDP} for tabular finite-horizon CMDPs. Our algorithm is motivated by the augmented Lagrangian method and can be performed efficiently. We show that during $K$ episodes of exploring the CMDP, our algorithm obtains a regret of $\tilde{O}(\sqrt{K})$ for both the objective and the constraint violation. Unlike existing Lagrangian approaches, our algorithm achieves this regret without the need for the cancellation of errors.

Multi-Player Bandits: The Adversarial Case

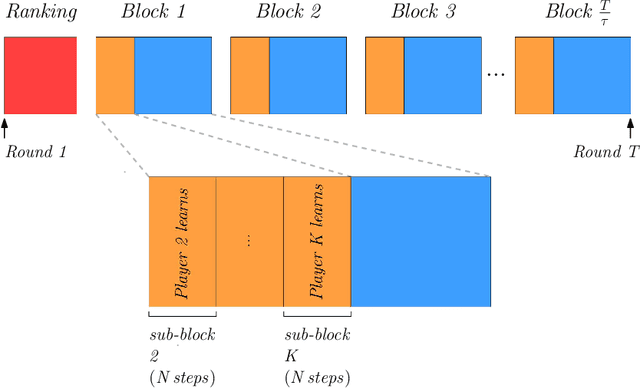
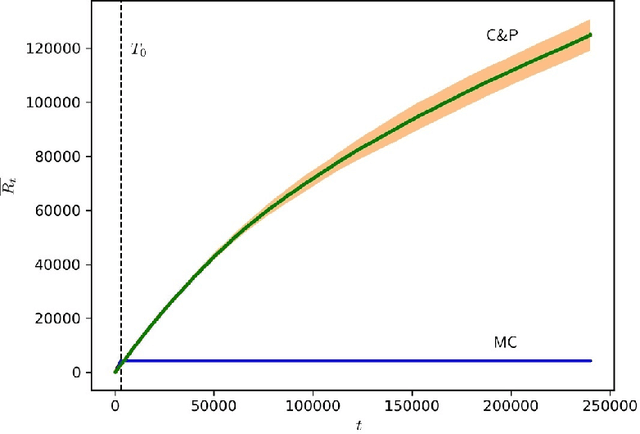
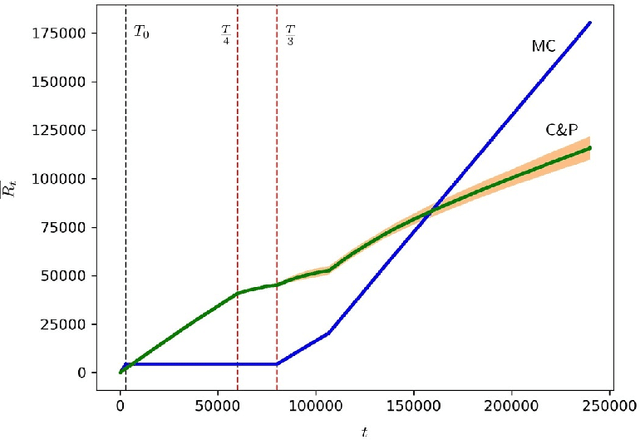
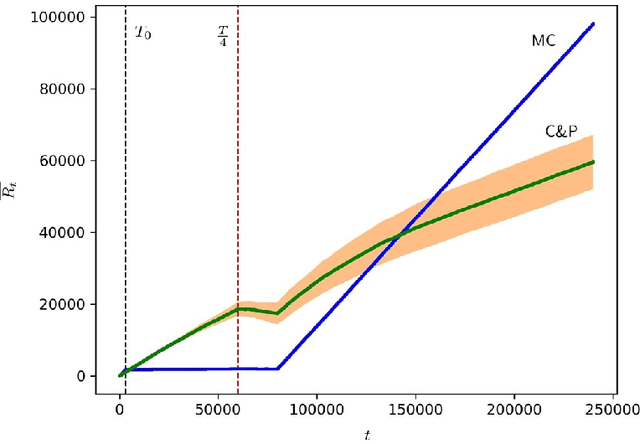
We consider a setting where multiple players sequentially choose among a common set of actions (arms). Motivated by a cognitive radio networks application, we assume that players incur a loss upon colliding, and that communication between players is not possible. Existing approaches assume that the system is stationary. Yet this assumption is often violated in practice, e.g., due to signal strength fluctuations. In this work, we design the first Multi-player Bandit algorithm that provably works in arbitrarily changing environments, where the losses of the arms may even be chosen by an adversary. This resolves an open problem posed by Rosenski, Shamir, and Szlak (2016).