Adrian Müller
Best of Both Worlds: Regret Minimization versus Minimax Play
Feb 17, 2025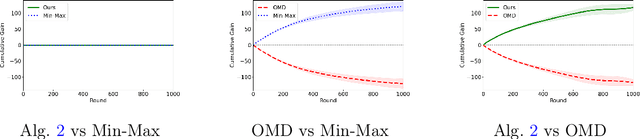


Abstract:In this paper, we investigate the existence of online learning algorithms with bandit feedback that simultaneously guarantee $O(1)$ regret compared to a given comparator strategy, and $O(\sqrt{T})$ regret compared to the best strategy in hindsight, where $T$ is the number of rounds. We provide the first affirmative answer to this question. In the context of symmetric zero-sum games, both in normal- and extensive form, we show that our results allow us to guarantee to risk at most $O(1)$ loss while being able to gain $\Omega(T)$ from exploitable opponents, thereby combining the benefits of both no-regret algorithms and minimax play.
Truly No-Regret Learning in Constrained MDPs
Feb 24, 2024Abstract:Constrained Markov decision processes (CMDPs) are a common way to model safety constraints in reinforcement learning. State-of-the-art methods for efficiently solving CMDPs are based on primal-dual algorithms. For these algorithms, all currently known regret bounds allow for error cancellations -- one can compensate for a constraint violation in one round with a strict constraint satisfaction in another. This makes the online learning process unsafe since it only guarantees safety for the final (mixture) policy but not during learning. As Efroni et al. (2020) pointed out, it is an open question whether primal-dual algorithms can provably achieve sublinear regret if we do not allow error cancellations. In this paper, we give the first affirmative answer. We first generalize a result on last-iterate convergence of regularized primal-dual schemes to CMDPs with multiple constraints. Building upon this insight, we propose a model-based primal-dual algorithm to learn in an unknown CMDP. We prove that our algorithm achieves sublinear regret without error cancellations.
Cancellation-Free Regret Bounds for Lagrangian Approaches in Constrained Markov Decision Processes
Jun 12, 2023
Abstract:Constrained Markov Decision Processes (CMDPs) are one of the common ways to model safe reinforcement learning problems, where the safety objectives are modeled by constraint functions. Lagrangian-based dual or primal-dual algorithms provide efficient methods for learning in CMDPs. For these algorithms, the currently known regret bounds in the finite-horizon setting allow for a \textit{cancellation of errors}; that is, one can compensate for a constraint violation in one episode with a strict constraint satisfaction in another episode. However, in practical applications, we do not consider such a behavior safe. In this paper, we overcome this weakness by proposing a novel model-based dual algorithm \textsc{OptAug-CMDP} for tabular finite-horizon CMDPs. Our algorithm is motivated by the augmented Lagrangian method and can be performed efficiently. We show that during $K$ episodes of exploring the CMDP, our algorithm obtains a regret of $\tilde{O}(\sqrt{K})$ for both the objective and the constraint violation. Unlike existing Lagrangian approaches, our algorithm achieves this regret without the need for the cancellation of errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge