Best of Both Worlds: Regret Minimization versus Minimax Play

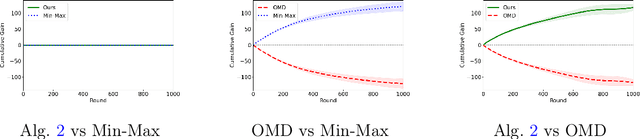
In this paper, we investigate the existence of online learning algorithms with bandit feedback that simultaneously guarantee $O(1)$ regret compared to a given comparator strategy, and $O(\sqrt{T})$ regret compared to the best strategy in hindsight, where $T$ is the number of rounds. We provide the first affirmative answer to this question. In the context of symmetric zero-sum games, both in normal- and extensive form, we show that our results allow us to guarantee to risk at most $O(1)$ loss while being able to gain $\Omega(T)$ from exploitable opponents, thereby combining the benefits of both no-regret algorithms and minimax play.