Jon Schneider
Coherence Mechanisms for Provable Self-Improvement
Nov 11, 2025Abstract:Self-improvement is a critical capability for large language models and other intelligent systems, enabling them to refine their behavior and internal consistency without external supervision. Despite its importance, prior approaches largely rely on empirical heuristics and lack formal guarantees. In this paper, we propose a principled framework for self-improvement based on the concept of \emph{coherence}, which requires that a model's outputs remain consistent under task-preserving transformations of the input. We formalize this concept using projection-based mechanisms that update a baseline model to be coherent while remaining as close as possible to its original behavior. We provide rigorous theoretical guarantees that these mechanisms achieve \emph{monotonic improvement}, measured by a reduction in expected Bregman divergence. Our analysis is comprehensive, covering both \emph{direct} and \emph{two-step} projection methods, and robustly extends these guarantees to non-realizable settings, empirical (finite-sample) distributions, and relaxed coherence constraints. Furthermore, we establish a general \emph{characterization theorem}, showing that any mechanism with similar provable improvement guarantees must inherently conform to a coherence-based structure. This culminates in rigidity results under the demand for universal improvement, establishing coherence as a fundamental and, in a formal sense, necessary principle for provable self-improvement.
High-Dimensional Calibration from Swap Regret
May 27, 2025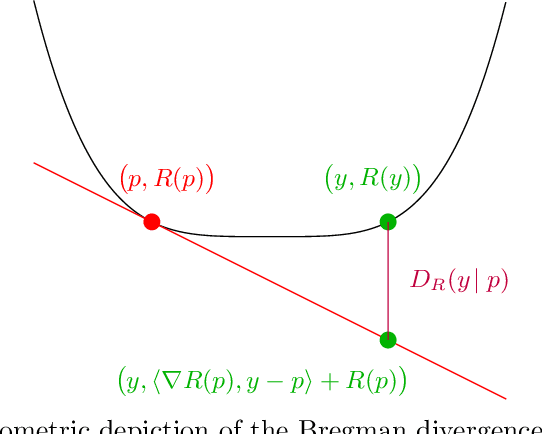
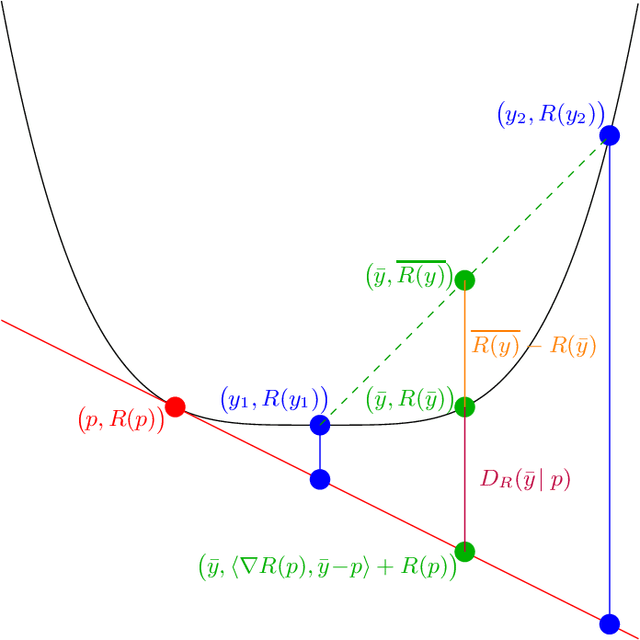

Abstract:We study the online calibration of multi-dimensional forecasts over an arbitrary convex set $\mathcal{P} \subset \mathbb{R}^d$ relative to an arbitrary norm $\Vert\cdot\Vert$. We connect this with the problem of external regret minimization for online linear optimization, showing that if it is possible to guarantee $O(\sqrt{\rho T})$ worst-case regret after $T$ rounds when actions are drawn from $\mathcal{P}$ and losses are drawn from the dual $\Vert \cdot \Vert_*$ unit norm ball, then it is also possible to obtain $\epsilon$-calibrated forecasts after $T = \exp(O(\rho /\epsilon^2))$ rounds. When $\mathcal{P}$ is the $d$-dimensional simplex and $\Vert \cdot \Vert$ is the $\ell_1$-norm, the existence of $O(\sqrt{T\log d})$-regret algorithms for learning with experts implies that it is possible to obtain $\epsilon$-calibrated forecasts after $T = \exp(O(\log{d}/\epsilon^2)) = d^{O(1/\epsilon^2)}$ rounds, recovering a recent result of Peng (2025). Interestingly, our algorithm obtains this guarantee without requiring access to any online linear optimization subroutine or knowledge of the optimal rate $\rho$ -- in fact, our algorithm is identical for every setting of $\mathcal{P}$ and $\Vert \cdot \Vert$. Instead, we show that the optimal regularizer for the above OLO problem can be used to upper bound the above calibration error by a swap regret, which we then minimize by running the recent TreeSwap algorithm with Follow-The-Leader as a subroutine. Finally, we prove that any online calibration algorithm that guarantees $\epsilon T$ $\ell_1$-calibration error over the $d$-dimensional simplex requires $T \geq \exp(\mathrm{poly}(1/\epsilon))$ (assuming $d \geq \mathrm{poly}(1/\epsilon)$). This strengthens the corresponding $d^{\Omega(\log{1/\epsilon})}$ lower bound of Peng, and shows that an exponential dependence on $1/\epsilon$ is necessary.
A New Benchmark for Online Learning with Budget-Balancing Constraints
Mar 19, 2025Abstract:The adversarial Bandit with Knapsack problem is a multi-armed bandits problem with budget constraints and adversarial rewards and costs. In each round, a learner selects an action to take and observes the reward and cost of the selected action. The goal is to maximize the sum of rewards while satisfying the budget constraint. The classical benchmark to compare against is the best fixed distribution over actions that satisfies the budget constraint in expectation. Unlike its stochastic counterpart, where rewards and costs are drawn from some fixed distribution (Badanidiyuru et al., 2018), the adversarial BwK problem does not admit a no-regret algorithm for every problem instance due to the "spend-or-save" dilemma (Immorlica et al., 2022). A key problem left open by existing works is whether there exists a weaker but still meaningful benchmark to compare against such that no-regret learning is still possible. In this work, we present a new benchmark to compare against, motivated both by real-world applications such as autobidding and by its underlying mathematical structure. The benchmark is based on the Earth Mover's Distance (EMD), and we show that sublinear regret is attainable against any strategy whose spending pattern is within EMD $o(T^2)$ of any sub-pacing spending pattern. As a special case, we obtain results against the "pacing over windows" benchmark, where we partition time into disjoint windows of size $w$ and allow the benchmark strategies to choose a different distribution over actions for each window while satisfying a pacing budget constraint. Against this benchmark, our algorithm obtains a regret bound of $\tilde{O}(T/\sqrt{w}+\sqrt{wT})$. We also show a matching lower bound, proving the optimality of our algorithm in this important special case. In addition, we provide further evidence of the necessity of the EMD condition for obtaining a sublinear regret.
Swap Regret and Correlated Equilibria Beyond Normal-Form Games
Feb 27, 2025Abstract:Swap regret is a notion that has proven itself to be central to the study of general-sum normal-form games, with swap-regret minimization leading to convergence to the set of correlated equilibria and guaranteeing non-manipulability against a self-interested opponent. However, the situation for more general classes of games -- such as Bayesian games and extensive-form games -- is less clear-cut, with multiple candidate definitions for swap-regret but no known efficiently minimizable variant of swap regret that implies analogous non-manipulability guarantees. In this paper, we present a new variant of swap regret for polytope games that we call ``profile swap regret'', with the property that obtaining sublinear profile swap regret is both necessary and sufficient for any learning algorithm to be non-manipulable by an opponent (resolving an open problem of Mansour et al., 2022). Although we show profile swap regret is NP-hard to compute given a transcript of play, we show it is nonetheless possible to design efficient learning algorithms that guarantee at most $O(\sqrt{T})$ profile swap regret. Finally, we explore the correlated equilibrium notion induced by low-profile-swap-regret play, and demonstrate a gap between the set of outcomes that can be implemented by this learning process and the set of outcomes that can be implemented by a third-party mediator (in contrast to the situation in normal-form games).
Best of Both Worlds: Regret Minimization versus Minimax Play
Feb 17, 2025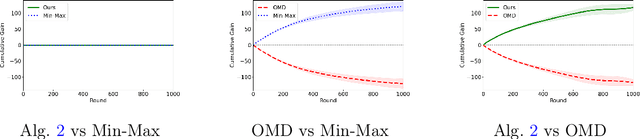


Abstract:In this paper, we investigate the existence of online learning algorithms with bandit feedback that simultaneously guarantee $O(1)$ regret compared to a given comparator strategy, and $O(\sqrt{T})$ regret compared to the best strategy in hindsight, where $T$ is the number of rounds. We provide the first affirmative answer to this question. In the context of symmetric zero-sum games, both in normal- and extensive form, we show that our results allow us to guarantee to risk at most $O(1)$ loss while being able to gain $\Omega(T)$ from exploitable opponents, thereby combining the benefits of both no-regret algorithms and minimax play.
Full Swap Regret and Discretized Calibration
Feb 13, 2025Abstract:We study the problem of minimizing swap regret in structured normal-form games. Players have a very large (potentially infinite) number of pure actions, but each action has an embedding into $d$-dimensional space and payoffs are given by bilinear functions of these embeddings. We provide an efficient learning algorithm for this setting that incurs at most $\tilde{O}(T^{(d+1)/(d+3)})$ swap regret after $T$ rounds. To achieve this, we introduce a new online learning problem we call \emph{full swap regret minimization}. In this problem, a learner repeatedly takes a (randomized) action in a bounded convex $d$-dimensional action set $\mathcal{K}$ and then receives a loss from the adversary, with the goal of minimizing their regret with respect to the \emph{worst-case} swap function mapping $\mathcal{K}$ to $\mathcal{K}$. For varied assumptions about the convexity and smoothness of the loss functions, we design algorithms with full swap regret bounds ranging from $O(T^{d/(d+2)})$ to $O(T^{(d+1)/(d+2)})$. Finally, we apply these tools to the problem of online forecasting to minimize calibration error, showing that several notions of calibration can be viewed as specific instances of full swap regret. In particular, we design efficient algorithms for online forecasting that guarantee at most $O(T^{1/3})$ $\ell_2$-calibration error and $O(\max(\sqrt{\epsilon T}, T^{1/3}))$ \emph{discretized-calibration} error (when the forecaster is restricted to predicting multiples of $\epsilon$).
Learning to Play Against Unknown Opponents
Dec 24, 2024
Abstract:We consider the problem of a learning agent who has to repeatedly play a general sum game against a strategic opponent who acts to maximize their own payoff by optimally responding against the learner's algorithm. The learning agent knows their own payoff function, but is uncertain about the payoff of their opponent (knowing only that it is drawn from some distribution $\mathcal{D}$). What learning algorithm should the agent run in order to maximize their own total utility? We demonstrate how to construct an $\varepsilon$-optimal learning algorithm (obtaining average utility within $\varepsilon$ of the optimal utility) for this problem in time polynomial in the size of the input and $1/\varepsilon$ when either the size of the game or the support of $\mathcal{D}$ is constant. When the learning algorithm is further constrained to be a no-regret algorithm, we demonstrate how to efficiently construct an optimal learning algorithm (asymptotically achieving the optimal utility) in polynomial time, independent of any other assumptions. Both results make use of recently developed machinery that converts the analysis of learning algorithms to the study of the class of corresponding geometric objects known as menus.
Computing Optimal Regularizers for Online Linear Optimization
Oct 22, 2024Abstract:Follow-the-Regularized-Leader (FTRL) algorithms are a popular class of learning algorithms for online linear optimization (OLO) that guarantee sub-linear regret, but the choice of regularizer can significantly impact dimension-dependent factors in the regret bound. We present an algorithm that takes as input convex and symmetric action sets and loss sets for a specific OLO instance, and outputs a regularizer such that running FTRL with this regularizer guarantees regret within a universal constant factor of the best possible regret bound. In particular, for any choice of (convex, symmetric) action set and loss set we prove that there exists an instantiation of FTRL which achieves regret within a constant factor of the best possible learning algorithm, strengthening the universality result of Srebro et al., 2011. Our algorithm requires preprocessing time and space exponential in the dimension $d$ of the OLO instance, but can be run efficiently online assuming a membership and linear optimization oracle for the action and loss sets, respectively (and is fully polynomial time for the case of constant dimension $d$). We complement this with a lower bound showing that even deciding whether a given regularizer is $\alpha$-strongly-convex with respect to a given norm is NP-hard.
Adversarial Online Learning with Temporal Feedback Graphs
Jun 30, 2024Abstract:We study a variant of prediction with expert advice where the learner's action at round $t$ is only allowed to depend on losses on a specific subset of the rounds (where the structure of which rounds' losses are visible at time $t$ is provided by a directed "feedback graph" known to the learner). We present a novel learning algorithm for this setting based on a strategy of partitioning the losses across sub-cliques of this graph. We complement this with a lower bound that is tight in many practical settings, and which we conjecture to be within a constant factor of optimal. For the important class of transitive feedback graphs, we prove that this algorithm is efficiently implementable and obtains the optimal regret bound (up to a universal constant).
Rate-Preserving Reductions for Blackwell Approachability
Jun 10, 2024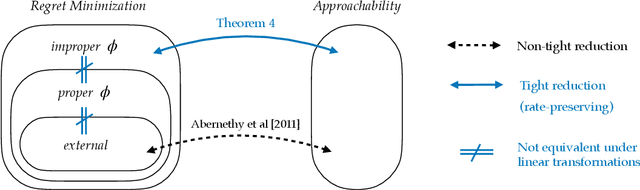
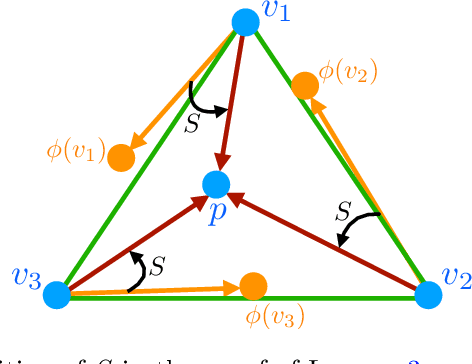
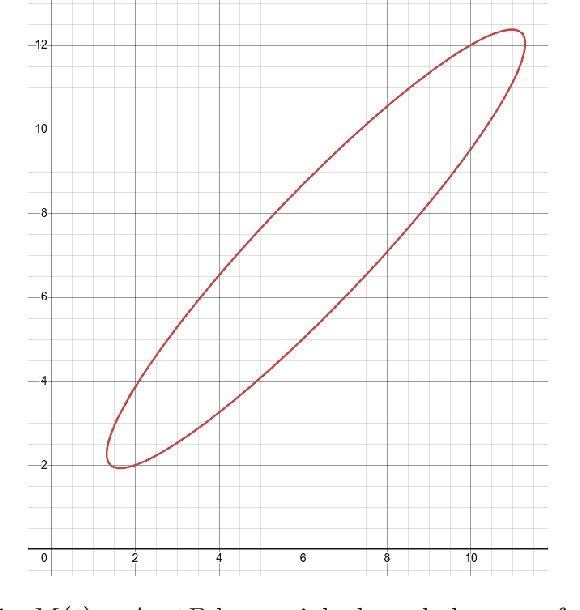
Abstract:Abernethy et al. (2011) showed that Blackwell approachability and no-regret learning are equivalent, in the sense that any algorithm that solves a specific Blackwell approachability instance can be converted to a sublinear regret algorithm for a specific no-regret learning instance, and vice versa. In this paper, we study a more fine-grained form of such reductions, and ask when this translation between problems preserves not only a sublinear rate of convergence, but also preserves the optimal rate of convergence. That is, in which cases does it suffice to find the optimal regret bound for a no-regret learning instance in order to find the optimal rate of convergence for a corresponding approachability instance? We show that the reduction of Abernethy et al. (2011) does not preserve rates: their reduction may reduce a $d$-dimensional approachability instance $I_1$ with optimal convergence rate $R_1$ to a no-regret learning instance $I_2$ with optimal regret-per-round of $R_2$, with $R_{2}/R_{1}$ arbitrarily large (in particular, it is possible that $R_1 = 0$ and $R_{2} > 0$). On the other hand, we show that it is possible to tightly reduce any approachability instance to an instance of a generalized form of regret minimization we call improper $\phi$-regret minimization (a variant of the $\phi$-regret minimization of Gordon et al. (2008) where the transformation functions may map actions outside of the action set). Finally, we characterize when linear transformations suffice to reduce improper $\phi$-regret minimization problems to standard classes of regret minimization problems in a rate preserving manner. We prove that some improper $\phi$-regret minimization instances cannot be reduced to either subclass of instance in this way, suggesting that approachability can capture some problems that cannot be phrased in the language of online learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge