Understanding Influence Functions and Datamodels via Harmonic Analysis

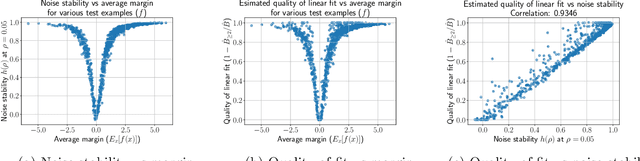
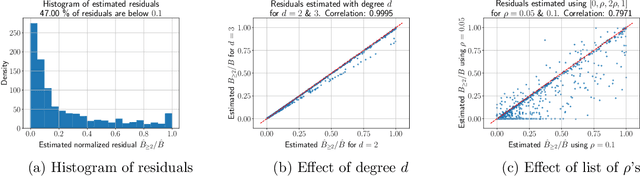
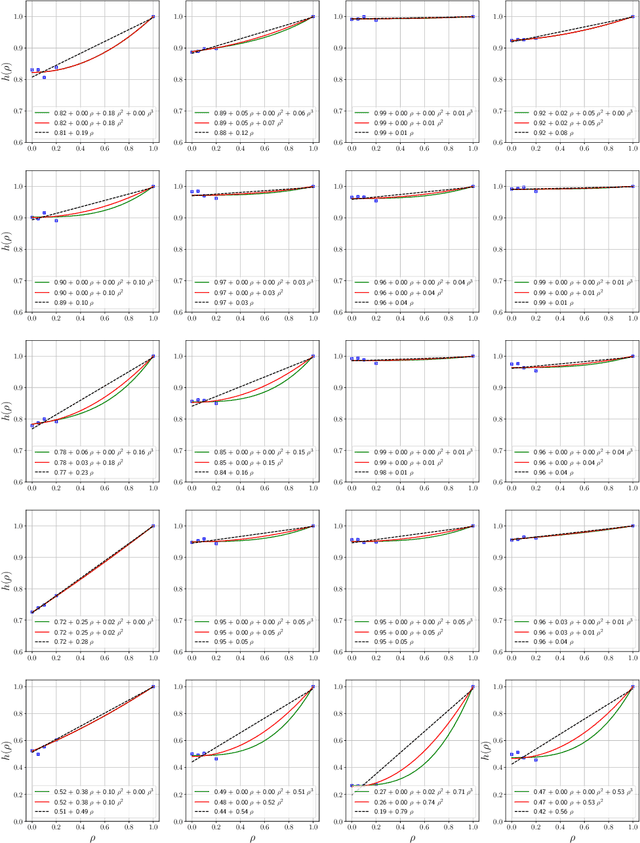
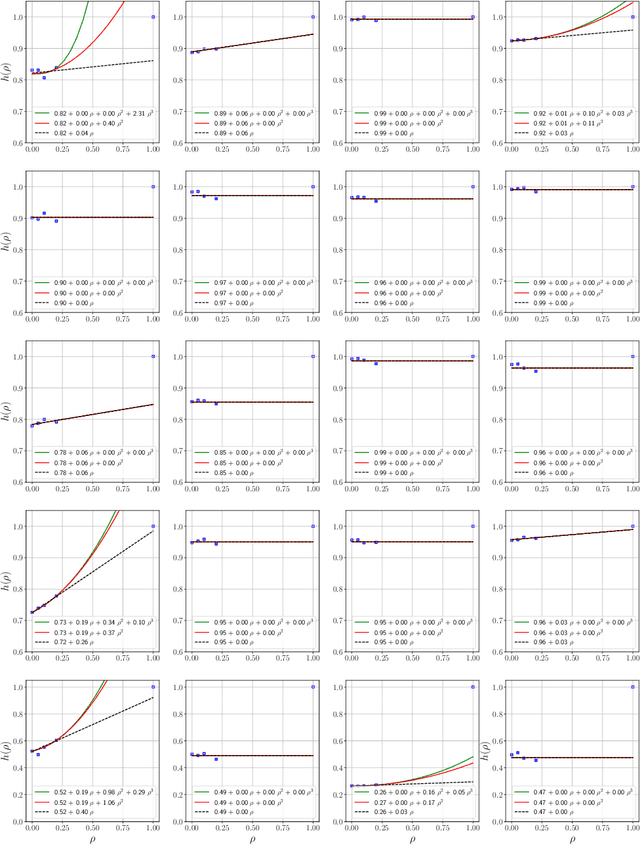
Influence functions estimate effect of individual data points on predictions of the model on test data and were adapted to deep learning in Koh and Liang [2017]. They have been used for detecting data poisoning, detecting helpful and harmful examples, influence of groups of datapoints, etc. Recently, Ilyas et al. [2022] introduced a linear regression method they termed datamodels to predict the effect of training points on outputs on test data. The current paper seeks to provide a better theoretical understanding of such interesting empirical phenomena. The primary tool is harmonic analysis and the idea of noise stability. Contributions include: (a) Exact characterization of the learnt datamodel in terms of Fourier coefficients. (b) An efficient method to estimate the residual error and quality of the optimum linear datamodel without having to train the datamodel. (c) New insights into when influences of groups of datapoints may or may not add up linearly.

Statistically Near-Optimal Hypothesis Selection

Hypothesis Selection is a fundamental distribution learning problem where given a comparator-class $Q=\{q_1,\ldots, q_n\}$ of distributions, and a sampling access to an unknown target distribution $p$, the goal is to output a distribution $q$ such that $\mathsf{TV}(p,q)$ is close to $opt$, where $opt = \min_i\{\mathsf{TV}(p,q_i)\}$ and $\mathsf{TV}(\cdot, \cdot)$ denotes the total-variation distance. Despite the fact that this problem has been studied since the 19th century, its complexity in terms of basic resources, such as number of samples and approximation guarantees, remains unsettled (this is discussed, e.g., in the charming book by Devroye and Lugosi `00). This is in stark contrast with other (younger) learning settings, such as PAC learning, for which these complexities are well understood. We derive an optimal $2$-approximation learning strategy for the Hypothesis Selection problem, outputting $q$ such that $\mathsf{TV}(p,q) \leq2 \cdot opt + \eps$, with a (nearly) optimal sample complexity of~$\tilde O(\log n/\epsilon^2)$. This is the first algorithm that simultaneously achieves the best approximation factor and sample complexity: previously, Bousquet, Kane, and Moran (COLT `19) gave a learner achieving the optimal $2$-approximation, but with an exponentially worse sample complexity of $\tilde O(\sqrt{n}/\epsilon^{2.5})$, and Yatracos~(Annals of Statistics `85) gave a learner with optimal sample complexity of $O(\log n /\epsilon^2)$ but with a sub-optimal approximation factor of $3$.

Optimization-friendly generic mechanisms without money

The goal of this paper is to develop a generic framework for converting modern optimization algorithms into mechanisms where inputs come from self-interested agents. We focus on aggregating preferences from $n$ players in a context without money. Special cases of this setting include voting, allocation of items by lottery, and matching. Our key technical contribution is a new meta-algorithm we call \apex (Adaptive Pricing Equalizing Externalities). The framework is sufficiently general to be combined with any optimization algorithm that is based on local search. We outline an agenda for studying the algorithm's properties and its applications. As a special case of applying the framework to the problem of one-sided assignment with lotteries, we obtain a strengthening of the 1979 result by Hylland and Zeckhauser on allocation via a competitive equilibrium from equal incomes (CEEI). The [HZ79] result posits that there is a (fractional) allocation and a set of item prices such that the allocation is a competitive equilibrium given prices. We further show that there is always a reweighing of the players' utility values such that running unit-demand VCG with reweighed utilities leads to a HZ-equilibrium prices. Interestingly, not all HZ competitive equilibria come from VCG prices. As part of our proof, we re-prove the [HZ79] result using only Brouwer's fixed point theorem (and not the more general Kakutani's theorem). This may be of independent interest.

The Role of Randomness and Noise in Strategic Classification

We investigate the problem of designing optimal classifiers in the strategic classification setting, where the classification is part of a game in which players can modify their features to attain a favorable classification outcome (while incurring some cost). Previously, the problem has been considered from a learning-theoretic perspective and from the algorithmic fairness perspective. Our main contributions include 1. Showing that if the objective is to maximize the efficiency of the classification process (defined as the accuracy of the outcome minus the sunk cost of the qualified players manipulating their features to gain a better outcome), then using randomized classifiers (that is, ones where the probability of a given feature vector to be accepted by the classifier is strictly between 0 and 1) is necessary. 2. Showing that in many natural cases, the imposed optimal solution (in terms of efficiency) has the structure where players never change their feature vectors (the randomized classifier is structured in a way, such that the gain in the probability of being classified as a 1 does not justify the expense of changing one's features). 3. Observing that the randomized classification is not a stable best-response from the classifier's viewpoint, and that the classifier doesn't benefit from randomized classifiers without creating instability in the system. 4. Showing that in some cases, a noisier signal leads to better equilibria outcomes -- improving both accuracy and fairness when more than one subpopulation with different feature adjustment costs are involved. This is interesting from a policy perspective, since it is hard to force institutions to stick to a particular randomized classification strategy (especially in a context of a market with multiple classifiers), but it is possible to alter the information environment to make the feature signals inherently noisier.

The gradient complexity of linear regression

We investigate the computational complexity of several basic linear algebra primitives, including largest eigenvector computation and linear regression, in the computational model that allows access to the data via a matrix-vector product oracle. We show that for polynomial accuracy, $\Theta(d)$ calls to the oracle are necessary and sufficient even for a randomized algorithm. Our lower bound is based on a reduction to estimating the least eigenvalue of a random Wishart matrix. This simple distribution enables a concise proof, leveraging a few key properties of the random Wishart ensemble.

Convex Set Disjointness, Distributed Learning of Halfspaces, and LP Feasibility

We study the Convex Set Disjointness (CSD) problem, where two players have input sets taken from an arbitrary fixed domain~$U\subseteq \mathbb{R}^d$ of size $\lvert U\rvert = n$. Their mutual goal is to decide using minimum communication whether the convex hulls of their sets intersect (equivalently, whether their sets can be separated by a hyperplane). Different forms of this problem naturally arise in distributed learning and optimization: it is equivalent to {\em Distributed Linear Program (LP) Feasibility} -- a basic task in distributed optimization, and it is tightly linked to {\it Distributed Learning of Halfdpaces in $\mathbb{R}^d$}. In {communication complexity theory}, CSD can be viewed as a geometric interpolation between the classical problems of {Set Disjointness} (when~$d\geq n-1$) and {Greater-Than} (when $d=1$). We establish a nearly tight bound of $\tilde \Theta(d\log n)$ on the communication complexity of learning halfspaces in $\mathbb{R}^d$. For Convex Set Disjointness (and the equivalent task of distributed LP feasibility) we derive upper and lower bounds of $\tilde O(d^2\log n)$ and~$\Omega(d\log n)$. These results improve upon several previous works in distributed learning and optimization. Unlike typical works in communication complexity, the main technical contribution of this work lies in the upper bounds. In particular, our protocols are based on a {\it Container Lemma for Halfspaces} and on two variants of {\it Carath\'eodory's Theorem}, which may be of independent interest. These geometric statements are used by our protocols to provide a compressed summary of the players' input.

Sorted Top-k in Rounds

We consider the sorted top-$k$ problem whose goal is to recover the top-$k$ items with the correct order out of $n$ items using pairwise comparisons. In many applications, multiple rounds of interaction can be costly. We restrict our attention to algorithms with a constant number of rounds $r$ and try to minimize the sample complexity, i.e. the number of comparisons. When the comparisons are noiseless, we characterize how the optimal sample complexity depends on the number of rounds (up to a polylogarithmic factor for general $r$ and up to a constant factor for $r=1$ or 2). In particular, the sample complexity is $\Theta(n^2)$ for $r=1$, $\Theta(n\sqrt{k} + n^{4/3})$ for $r=2$ and $\tilde{\Theta}\left(n^{2/r} k^{(r-1)/r} + n\right)$ for $r \geq 3$. We extend our results of sorted top-$k$ to the noisy case where each comparison is correct with probability $2/3$. When $r=1$ or 2, we show that the sample complexity gets an extra $\Theta(\log(k))$ factor when we transition from the noiseless case to the noisy case. We also prove new results for top-$k$ and sorting in the noisy case. We believe our techniques can be generally useful for understanding the trade-off between round complexities and sample complexities of rank aggregation problems.

Calibration, Entropy Rates, and Memory in Language Models

Building accurate language models that capture meaningful long-term dependencies is a core challenge in natural language processing. Towards this end, we present a calibration-based approach to measure long-term discrepancies between a generative sequence model and the true distribution, and use these discrepancies to improve the model. Empirically, we show that state-of-the-art language models, including LSTMs and Transformers, are \emph{miscalibrated}: the entropy rates of their generations drift dramatically upward over time. We then provide provable methods to mitigate this phenomenon. Furthermore, we show how this calibration-based approach can also be used to measure the amount of memory that language models use for prediction.

Selling to a No-Regret Buyer

We consider the problem of a single seller repeatedly selling a single item to a single buyer (specifically, the buyer has a value drawn fresh from known distribution $D$ in every round). Prior work assumes that the buyer is fully rational and will perfectly reason about how their bids today affect the seller's decisions tomorrow. In this work we initiate a different direction: the buyer simply runs a no-regret learning algorithm over possible bids. We provide a fairly complete characterization of optimal auctions for the seller in this domain. Specifically: - If the buyer bids according to EXP3 (or any "mean-based" learning algorithm), then the seller can extract expected revenue arbitrarily close to the expected welfare. This auction is independent of the buyer's valuation $D$, but somewhat unnatural as it is sometimes in the buyer's interest to overbid. - There exists a learning algorithm $\mathcal{A}$ such that if the buyer bids according to $\mathcal{A}$ then the optimal strategy for the seller is simply to post the Myerson reserve for $D$ every round. - If the buyer bids according to EXP3 (or any "mean-based" learning algorithm), but the seller is restricted to "natural" auction formats where overbidding is dominated (e.g. Generalized First-Price or Generalized Second-Price), then the optimal strategy for the seller is a pay-your-bid format with decreasing reserves over time. Moreover, the seller's optimal achievable revenue is characterized by a linear program, and can be unboundedly better than the best truthful auction yet simultaneously unboundedly worse than the expected welfare.

Multi-armed Bandit Problems with Strategic Arms

We study a strategic version of the multi-armed bandit problem, where each arm is an individual strategic agent and we, the principal, pull one arm each round. When pulled, the arm receives some private reward $v_a$ and can choose an amount $x_a$ to pass on to the principal (keeping $v_a-x_a$ for itself). All non-pulled arms get reward $0$. Each strategic arm tries to maximize its own utility over the course of $T$ rounds. Our goal is to design an algorithm for the principal incentivizing these arms to pass on as much of their private rewards as possible. When private rewards are stochastically drawn each round ($v_a^t \leftarrow D_a$), we show that: - Algorithms that perform well in the classic adversarial multi-armed bandit setting necessarily perform poorly: For all algorithms that guarantee low regret in an adversarial setting, there exist distributions $D_1,\ldots,D_k$ and an approximate Nash equilibrium for the arms where the principal receives reward $o(T)$. - Still, there exists an algorithm for the principal that induces a game among the arms where each arm has a dominant strategy. When each arm plays its dominant strategy, the principal sees expected reward $\mu'T - o(T)$, where $\mu'$ is the second-largest of the means $\mathbb{E}[D_{a}]$. This algorithm maintains its guarantee if the arms are non-strategic ($x_a = v_a$), and also if there is a mix of strategic and non-strategic arms.