Multiplayer Bandit Learning, from Competition to Cooperation

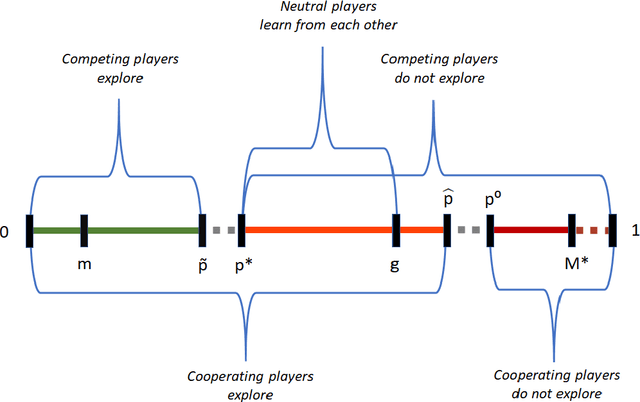
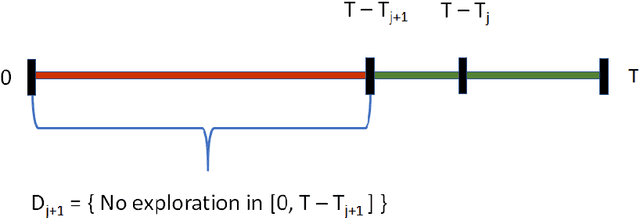
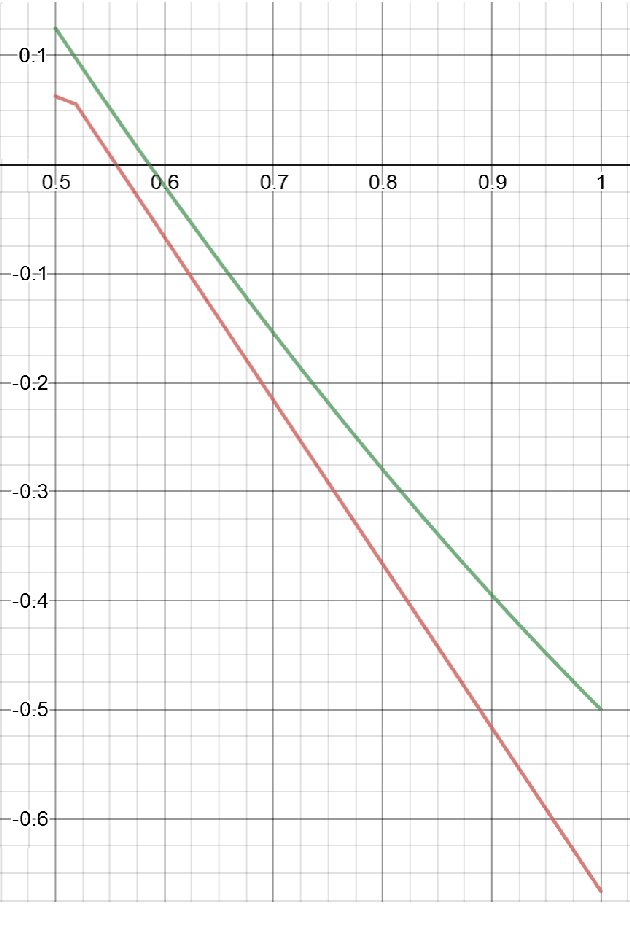
The stochastic multi-armed bandit problem is a classic model illustrating the tradeoff between exploration and exploitation. We study the effects of competition and cooperation on this tradeoff. Suppose there are $k$ arms and two players, Alice and Bob. In every round, each player pulls an arm, receives the resulting reward, and observes the choice of the other player but not their reward. Alice's utility is $\Gamma_A + \lambda \Gamma_B$ (and similarly for Bob), where $\Gamma_A$ is Alice's total reward and $\lambda \in [-1,1]$ is a cooperation parameter. At $\lambda = -1$ the players are competing in a zero-sum game, at $\lambda = 1$, they are fully cooperating, and at $\lambda = 0$, they are neutral: each player's utility is their own reward. The model is related to the economics literature on strategic experimentation, where usually the players observe each other's rewards. In the discounted setting, the Gittins index reduces the one-player problem to the comparison between a risky arm, with a prior $\mu$, and a predictable arm with success probability $p$. The value of $p$ where the player is indifferent between the arms is the Gittins index $g(\mu,\beta) > m$, where $m$ is the mean of the risky arm and $\beta$ the discount factor. We show that competing players explore less than a single player: there is $p^* \in (m, g(\mu, \beta))$ so that for all $p > p^*$, the players stay at the predictable arm. However, the players are not completely myopic: they still explore for some $p > m$. On the other hand, cooperating players explore more than a single player. Finally, we show that neutral players learn from each other, receiving strictly higher total rewards than they would playing alone, for all $ p\in (p^*, g(\mu,\beta))$, where $p^*$ is the threshold above which competing players do not explore. We show similar phenomena in the finite horizon setting.

Sorted Top-k in Rounds

We consider the sorted top-$k$ problem whose goal is to recover the top-$k$ items with the correct order out of $n$ items using pairwise comparisons. In many applications, multiple rounds of interaction can be costly. We restrict our attention to algorithms with a constant number of rounds $r$ and try to minimize the sample complexity, i.e. the number of comparisons. When the comparisons are noiseless, we characterize how the optimal sample complexity depends on the number of rounds (up to a polylogarithmic factor for general $r$ and up to a constant factor for $r=1$ or 2). In particular, the sample complexity is $\Theta(n^2)$ for $r=1$, $\Theta(n\sqrt{k} + n^{4/3})$ for $r=2$ and $\tilde{\Theta}\left(n^{2/r} k^{(r-1)/r} + n\right)$ for $r \geq 3$. We extend our results of sorted top-$k$ to the noisy case where each comparison is correct with probability $2/3$. When $r=1$ or 2, we show that the sample complexity gets an extra $\Theta(\log(k))$ factor when we transition from the noiseless case to the noisy case. We also prove new results for top-$k$ and sorting in the noisy case. We believe our techniques can be generally useful for understanding the trade-off between round complexities and sample complexities of rank aggregation problems.

Non-Stochastic Multi-Player Multi-Armed Bandits: Optimal Rate With Collision Information, Sublinear Without

We consider the non-stochastic version of the (cooperative) multi-player multi-armed bandit problem. The model assumes no communication at all between the players, and furthermore when two (or more) players select the same action this results in a maximal loss. We prove the first $\sqrt{T}$-type regret guarantee for this problem, under the feedback model where collisions are announced to the colliding players. Such a bound was not known even for the simpler stochastic version. We also prove the first sublinear guarantee for the feedback model where collision information is not available, namely $T^{1-\frac{1}{2m}}$ where $m$ is the number of players.

Online Learning with an Almost Perfect Expert

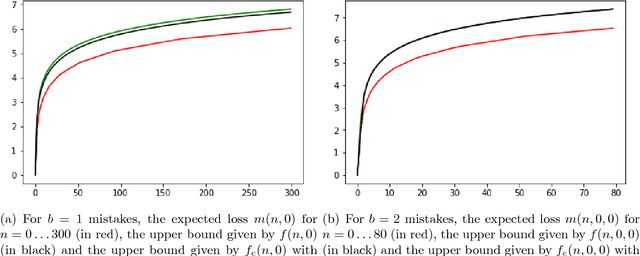
We study the multiclass online learning problem where a forecaster makes a sequence of predictions using the advice of $n$ experts. Our main contribution is to analyze the regime where the best expert makes at most $b$ mistakes and to show that when $b = o(\log_4{n})$, the expected number of mistakes made by the optimal forecaster is at most $\log_4{n} + o(\log_4{n})$. We also describe an adversary strategy showing that this bound is tight and that the worst case is attained for binary prediction.

Mixing time estimation in reversible Markov chains from a single sample path

The spectral gap $\gamma$ of a finite, ergodic, and reversible Markov chain is an important parameter measuring the asymptotic rate of convergence. In applications, the transition matrix $P$ may be unknown, yet one sample of the chain up to a fixed time $n$ may be observed. We consider here the problem of estimating $\gamma$ from this data. Let $\pi$ be the stationary distribution of $P$, and $\pi_\star = \min_x \pi(x)$. We show that if $n = \tilde{O}\bigl(\frac{1}{\gamma \pi_\star}\bigr)$, then $\gamma$ can be estimated to within multiplicative constants with high probability. When $\pi$ is uniform on $d$ states, this matches (up to logarithmic correction) a lower bound of $\tilde{\Omega}\bigl(\frac{d}{\gamma}\bigr)$ steps required for precise estimation of $\gamma$. Moreover, we provide the first procedure for computing a fully data-dependent interval, from a single finite-length trajectory of the chain, that traps the mixing time $t_{\text{mix}}$ of the chain at a prescribed confidence level. The interval does not require the knowledge of any parameters of the chain. This stands in contrast to previous approaches, which either only provide point estimates, or require a reset mechanism, or additional prior knowledge. The interval is constructed around the relaxation time $t_{\text{relax}} = 1/\gamma$, which is strongly related to the mixing time, and the width of the interval converges to zero roughly at a $1/\sqrt{n}$ rate, where $n$ is the length of the sample path.

Tight Lower Bounds for Multiplicative Weights Algorithmic Families

We study the fundamental problem of prediction with expert advice and develop regret lower bounds for a large family of algorithms for this problem. We develop simple adversarial primitives, that lend themselves to various combinations leading to sharp lower bounds for many algorithmic families. We use these primitives to show that the classic Multiplicative Weights Algorithm (MWA) has a regret of $\sqrt{\frac{T \ln k}{2}}$, there by completely closing the gap between upper and lower bounds. We further show a regret lower bound of $\frac{2}{3}\sqrt{\frac{T\ln k}{2}}$ for a much more general family of algorithms than MWA, where the learning rate can be arbitrarily varied over time, or even picked from arbitrary distributions over time. We also use our primitives to construct adversaries in the geometric horizon setting for MWA to precisely characterize the regret at $\frac{0.391}{\sqrt{\delta}}$ for the case of $2$ experts and a lower bound of $\frac{1}{2}\sqrt{\frac{\ln k}{2\delta}}$ for the case of arbitrary number of experts $k$.

Towards Optimal Algorithms for Prediction with Expert Advice

We study the classical problem of prediction with expert advice in the adversarial setting with a geometric stopping time. In 1965, Cover gave the optimal algorithm for the case of 2 experts. In this paper, we design the optimal algorithm, adversary and regret for the case of 3 experts. Further, we show that the optimal algorithm for $2$ and $3$ experts is a probability matching algorithm (analogous to Thompson sampling) against a particular randomized adversary. Remarkably, our proof shows that the probability matching algorithm is not only optimal against this particular randomized adversary, but also minimax optimal. Our analysis develops upper and lower bounds simultaneously, analogous to the primal-dual method. Our analysis of the optimal adversary goes through delicate asymptotics of the random walk of a particle between multiple walls. We use the connection we develop to random walks to derive an improved algorithm and regret bound for the case of $4$ experts, and, provide a general framework for designing the optimal algorithm and adversary for an arbitrary number of experts.

Approval Voting and Incentives in Crowdsourcing

The growing need for labeled training data has made crowdsourcing an important part of machine learning. The quality of crowdsourced labels is, however, adversely affected by three factors: (1) the workers are not experts; (2) the incentives of the workers are not aligned with those of the requesters; and (3) the interface does not allow workers to convey their knowledge accurately, by forcing them to make a single choice among a set of options. In this paper, we address these issues by introducing approval voting to utilize the expertise of workers who have partial knowledge of the true answer, and coupling it with a ("strictly proper") incentive-compatible compensation mechanism. We show rigorous theoretical guarantees of optimality of our mechanism together with a simple axiomatic characterization. We also conduct preliminary empirical studies on Amazon Mechanical Turk which validate our approach.

Bandit Convex Optimization: sqrt{T} Regret in One Dimension

We analyze the minimax regret of the adversarial bandit convex optimization problem. Focusing on the one-dimensional case, we prove that the minimax regret is $\widetilde\Theta(\sqrt{T})$ and partially resolve a decade-old open problem. Our analysis is non-constructive, as we do not present a concrete algorithm that attains this regret rate. Instead, we use minimax duality to reduce the problem to a Bayesian setting, where the convex loss functions are drawn from a worst-case distribution, and then we solve the Bayesian version of the problem with a variant of Thompson Sampling. Our analysis features a novel use of convexity, formalized as a "local-to-global" property of convex functions, that may be of independent interest.

Online Learning with Composite Loss Functions

We study a new class of online learning problems where each of the online algorithm's actions is assigned an adversarial value, and the loss of the algorithm at each step is a known and deterministic function of the values assigned to its recent actions. This class includes problems where the algorithm's loss is the minimum over the recent adversarial values, the maximum over the recent values, or a linear combination of the recent values. We analyze the minimax regret of this class of problems when the algorithm receives bandit feedback, and prove that when the minimum or maximum functions are used, the minimax regret is $\tilde \Omega(T^{2/3})$ (so called hard online learning problems), and when a linear function is used, the minimax regret is $\tilde O(\sqrt{T})$ (so called easy learning problems). Previously, the only online learning problem that was known to be provably hard was the multi-armed bandit with switching costs.