Simina Brânzei
Dueling Over Dessert, Mastering the Art of Repeated Cake Cutting
Feb 18, 2024Abstract:We consider the setting of repeated fair division between two players, denoted Alice and Bob, with private valuations over a cake. In each round, a new cake arrives, which is identical to the ones in previous rounds. Alice cuts the cake at a point of her choice, while Bob chooses the left piece or the right piece, leaving the remainder for Alice. We consider two versions: sequential, where Bob observes Alice's cut point before choosing left/right, and simultaneous, where he only observes her cut point after making his choice. The simultaneous version was first considered by Aumann and Maschler (1995). We observe that if Bob is almost myopic and chooses his favorite piece too often, then he can be systematically exploited by Alice through a strategy akin to a binary search. This strategy allows Alice to approximate Bob's preferences with increasing precision, thereby securing a disproportionate share of the resource over time. We analyze the limits of how much a player can exploit the other one and show that fair utility profiles are in fact achievable. Specifically, the players can enforce the equitable utility profile of $(1/2, 1/2)$ in the limit on every trajectory of play, by keeping the other player's utility to approximately $1/2$ on average while guaranteeing they themselves get at least approximately $1/2$ on average. We show this theorem using a connection with Blackwell approachability. Finally, we analyze a natural dynamic known as fictitious play, where players best respond to the empirical distribution of the other player. We show that fictitious play converges to the equitable utility profile of $(1/2, 1/2)$ at a rate of $O(1/\sqrt{T})$.
Online Learning in Multi-unit Auctions
May 27, 2023Abstract:We consider repeated multi-unit auctions with uniform pricing, which are widely used in practice for allocating goods such as carbon licenses. In each round, $K$ identical units of a good are sold to a group of buyers that have valuations with diminishing marginal returns. The buyers submit bids for the units, and then a price $p$ is set per unit so that all the units are sold. We consider two variants of the auction, where the price is set to the $K$-th highest bid and $(K+1)$-st highest bid, respectively. We analyze the properties of this auction in both the offline and online settings. In the offline setting, we consider the problem that one player $i$ is facing: given access to a data set that contains the bids submitted by competitors in past auctions, find a bid vector that maximizes player $i$'s cumulative utility on the data set. We design a polynomial time algorithm for this problem, by showing it is equivalent to finding a maximum-weight path on a carefully constructed directed acyclic graph. In the online setting, the players run learning algorithms to update their bids as they participate in the auction over time. Based on our offline algorithm, we design efficient online learning algorithms for bidding. The algorithms have sublinear regret, under both full information and bandit feedback structures. We complement our online learning algorithms with regret lower bounds. Finally, we analyze the quality of the equilibria in the worst case through the lens of the core solution concept in the game among the bidders. We show that the $(K+1)$-st price format is susceptible to collusion among the bidders; meanwhile, the $K$-th price format does not have this issue.
Multiplayer Bandit Learning, from Competition to Cooperation
Aug 03, 2019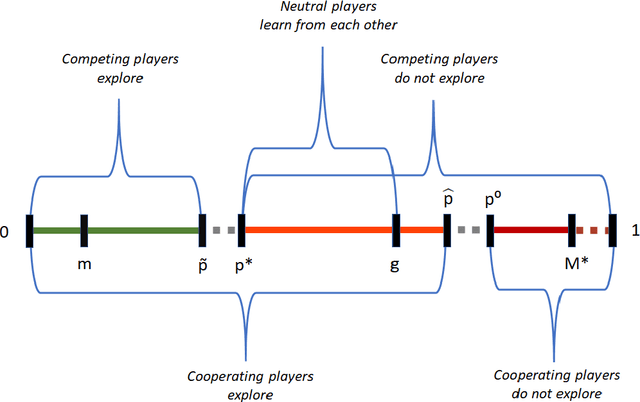
Abstract:The stochastic multi-armed bandit problem is a classic model illustrating the tradeoff between exploration and exploitation. We study the effects of competition and cooperation on this tradeoff. Suppose there are $k$ arms and two players, Alice and Bob. In every round, each player pulls an arm, receives the resulting reward, and observes the choice of the other player but not their reward. Alice's utility is $\Gamma_A + \lambda \Gamma_B$ (and similarly for Bob), where $\Gamma_A$ is Alice's total reward and $\lambda \in [-1,1]$ is a cooperation parameter. At $\lambda = -1$ the players are competing in a zero-sum game, at $\lambda = 1$, they are fully cooperating, and at $\lambda = 0$, they are neutral: each player's utility is their own reward. The model is related to the economics literature on strategic experimentation, where usually the players observe each other's rewards. In the discounted setting, the Gittins index reduces the one-player problem to the comparison between a risky arm, with a prior $\mu$, and a predictable arm with success probability $p$. The value of $p$ where the player is indifferent between the arms is the Gittins index $g(\mu,\beta) > m$, where $m$ is the mean of the risky arm and $\beta$ the discount factor. We show that competing players explore less than a single player: there is $p^* \in (m, g(\mu, \beta))$ so that for all $p > p^*$, the players stay at the predictable arm. However, the players are not completely myopic: they still explore for some $p > m$. On the other hand, cooperating players explore more than a single player. Finally, we show that neutral players learn from each other, receiving strictly higher total rewards than they would playing alone, for all $ p\in (p^*, g(\mu,\beta))$, where $p^*$ is the threshold above which competing players do not explore. We show similar phenomena in the finite horizon setting.
Online Learning with an Almost Perfect Expert
Sep 27, 2018
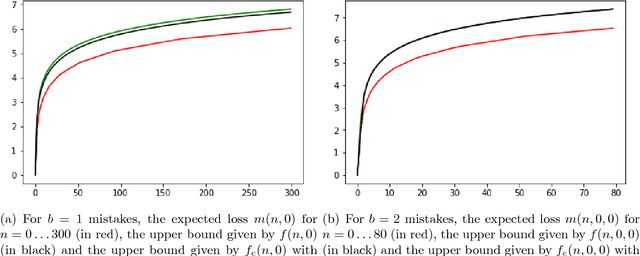
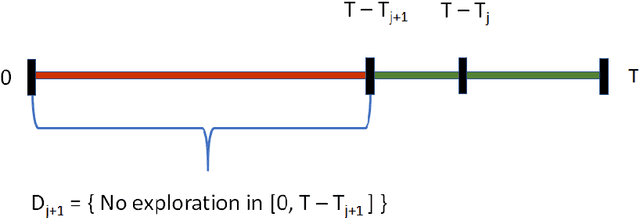
Abstract:We study the multiclass online learning problem where a forecaster makes a sequence of predictions using the advice of $n$ experts. Our main contribution is to analyze the regime where the best expert makes at most $b$ mistakes and to show that when $b = o(\log_4{n})$, the expected number of mistakes made by the optimal forecaster is at most $\log_4{n} + o(\log_4{n})$. We also describe an adversary strategy showing that this bound is tight and that the worst case is attained for binary prediction.
Weighted Clustering
Oct 04, 2016
Abstract:One of the most prominent challenges in clustering is "the user's dilemma," which is the problem of selecting an appropriate clustering algorithm for a specific task. A formal approach for addressing this problem relies on the identification of succinct, user-friendly properties that formally capture when certain clustering methods are preferred over others. Until now these properties focused on advantages of classical Linkage-Based algorithms, failing to identify when other clustering paradigms, such as popular center-based methods, are preferable. We present surprisingly simple new properties that delineate the differences between common clustering paradigms, which clearly and formally demonstrates advantages of center-based approaches for some applications. These properties address how sensitive algorithms are to changes in element frequencies, which we capture in a generalized setting where every element is associated with a real-valued weight.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge