Distribution Learnability and Robustness

We examine the relationship between learnability and robust (or agnostic) learnability for the problem of distribution learning. We show that, contrary to other learning settings (e.g., PAC learning of function classes), realizable learnability of a class of probability distributions does not imply its agnostic learnability. We go on to examine what type of data corruption can disrupt the learnability of a distribution class and what is such learnability robust against. We show that realizable learnability of a class of distributions implies its robust learnability with respect to only additive corruption, but not against subtractive corruption. We also explore related implications in the context of compression schemes and differentially private learnability.

Continual Learning: Applications and the Road Forward

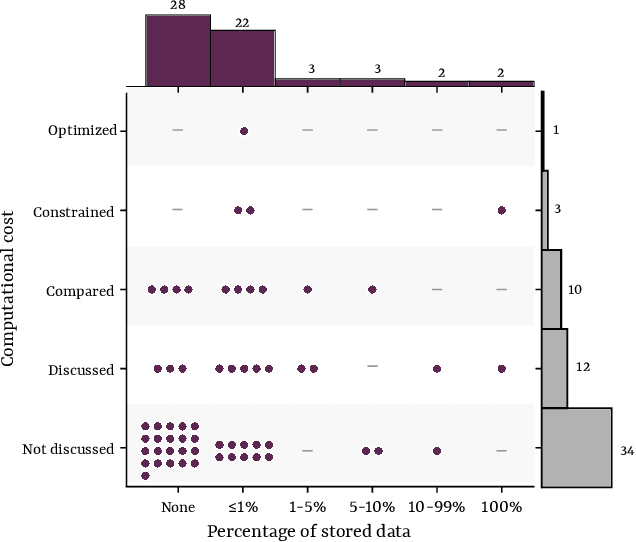
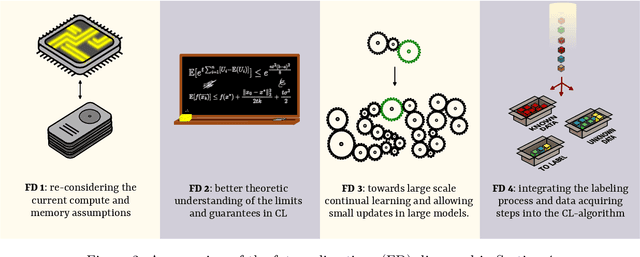
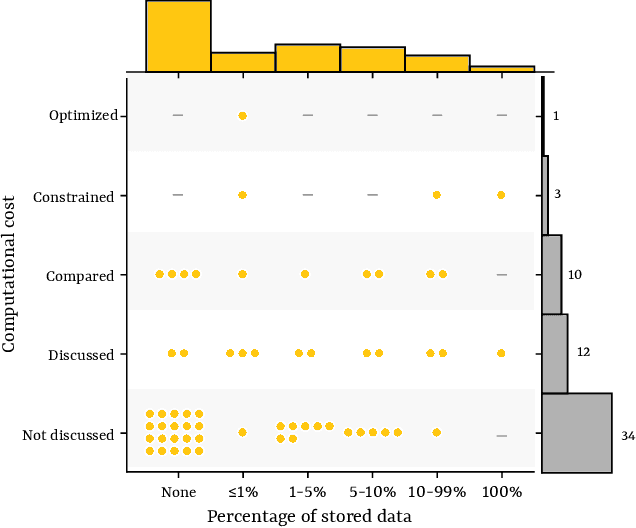
Continual learning is a sub-field of machine learning, which aims to allow machine learning models to continuously learn on new data, by accumulating knowledge without forgetting what was learned in the past. In this work, we take a step back, and ask: "Why should one care about continual learning in the first place?". We set the stage by surveying recent continual learning papers published at three major machine learning conferences, and show that memory-constrained settings dominate the field. Then, we discuss five open problems in machine learning, and even though they seem unrelated to continual learning at first sight, we show that continual learning will inevitably be part of their solution. These problems are model-editing, personalization, on-device learning, faster (re-)training and reinforcement learning. Finally, by comparing the desiderata from these unsolved problems and the current assumptions in continual learning, we highlight and discuss four future directions for continual learning research. We hope that this work offers an interesting perspective on the future of continual learning, while displaying its potential value and the paths we have to pursue in order to make it successful. This work is the result of the many discussions the authors had at the Dagstuhl seminar on Deep Continual Learning, in March 2023.

Private Distribution Learning with Public Data: The View from Sample Compression

We study the problem of private distribution learning with access to public data. In this setup, which we refer to as public-private learning, the learner is given public and private samples drawn from an unknown distribution $p$ belonging to a class $\mathcal Q$, with the goal of outputting an estimate of $p$ while adhering to privacy constraints (here, pure differential privacy) only with respect to the private samples. We show that the public-private learnability of a class $\mathcal Q$ is connected to the existence of a sample compression scheme for $\mathcal Q$, as well as to an intermediate notion we refer to as list learning. Leveraging this connection: (1) approximately recovers previous results on Gaussians over $\mathbb R^d$; and (2) leads to new ones, including sample complexity upper bounds for arbitrary $k$-mixtures of Gaussians over $\mathbb R^d$, results for agnostic and distribution-shift resistant learners, as well as closure properties for public-private learnability under taking mixtures and products of distributions. Finally, via the connection to list learning, we show that for Gaussians in $\mathbb R^d$, at least $d$ public samples are necessary for private learnability, which is close to the known upper bound of $d+1$ public samples.

On Computable Online Learning

We initiate a study of computable online (c-online) learning, which we analyze under varying requirements for "optimality" in terms of the mistake bound. Our main contribution is to give a necessary and sufficient condition for optimal c-online learning and show that the Littlestone dimension no longer characterizes the optimal mistake bound of c-online learning. Furthermore, we introduce anytime optimal (a-optimal) online learning, a more natural conceptualization of "optimality" and a generalization of Littlestone's Standard Optimal Algorithm. We show the existence of a computational separation between a-optimal and optimal online learning, proving that a-optimal online learning is computationally more difficult. Finally, we consider online learning with no requirements for optimality, and show, under a weaker notion of computability, that the finiteness of the Littlestone dimension no longer characterizes whether a class is c-online learnable with finite mistake bound. A potential avenue for strengthening this result is suggested by exploring the relationship between c-online and CPAC learning, where we show that c-online learning is as difficult as improper CPAC learning.

Impossibility results for fair representations

With the growing awareness to fairness in machine learning and the realization of the central role that data representation has in data processing tasks, there is an obvious interest in notions of fair data representations. The goal of such representations is that a model trained on data under the representation (e.g., a classifier) will be guaranteed to respect some fairness constraints. Such representations are useful when they can be fixed for training models on various different tasks and also when they serve as data filtering between the raw data (known to the representation designer) and potentially malicious agents that use the data under the representation to learn predictive models and make decisions. A long list of recent research papers strive to provide tools for achieving these goals. However, we prove that this is basically a futile effort. Roughly stated, we prove that no representation can guarantee the fairness of classifiers for different tasks trained using it; even the basic goal of achieving label-independent Demographic Parity fairness fails once the marginal data distribution shifts. More refined notions of fairness, like Odds Equality, cannot be guaranteed by a representation that does not take into account the task specific labeling rule with respect to which such fairness will be evaluated (even if the marginal data distribution is known a priory). Furthermore, except for trivial cases, no representation can guarantee Odds Equality fairness for any two different tasks, while allowing accurate label predictions for both. While some of our conclusions are intuitive, we formulate (and prove) crisp statements of such impossibilities, often contrasting impressions conveyed by many recent works on fair representations.

Enforcing Interpretability and its Statistical Impacts: Trade-offs between Accuracy and Interpretability

To date, there has been no formal study of the statistical cost of interpretability in machine learning. As such, the discourse around potential trade-offs is often informal and misconceptions abound. In this work, we aim to initiate a formal study of these trade-offs. A seemingly insurmountable roadblock is the lack of any agreed upon definition of interpretability. Instead, we propose a shift in perspective. Rather than attempt to define interpretability, we propose to model the \emph{act} of \emph{enforcing} interpretability. As a starting point, we focus on the setting of empirical risk minimization for binary classification, and view interpretability as a constraint placed on learning. That is, we assume we are given a subset of hypothesis that are deemed to be interpretable, possibly depending on the data distribution and other aspects of the context. We then model the act of enforcing interpretability as that of performing empirical risk minimization over the set of interpretable hypotheses. This model allows us to reason about the statistical implications of enforcing interpretability, using known results in statistical learning theory. Focusing on accuracy, we perform a case analysis, explaining why one may or may not observe a trade-off between accuracy and interpretability when the restriction to interpretable classifiers does or does not come at the cost of some excess statistical risk. We close with some worked examples and some open problems, which we hope will spur further theoretical development around the tradeoffs involved in interpretability.

When can unlabeled data improve the learning rate?

In semi-supervised classification, one is given access both to labeled and unlabeled data. As unlabeled data is typically cheaper to acquire than labeled data, this setup becomes advantageous as soon as one can exploit the unlabeled data in order to produce a better classifier than with labeled data alone. However, the conditions under which such an improvement is possible are not fully understood yet. Our analysis focuses on improvements in the minimax learning rate in terms of the number of labeled examples (with the number of unlabeled examples being allowed to depend on the number of labeled ones). We argue that for such improvements to be realistic and indisputable, certain specific conditions should be satisfied and previous analyses have failed to meet those conditions. We then demonstrate examples where these conditions can be met, in particular showing rate changes from $1/\sqrt{\ell}$ to $e^{-c\ell}$ and from $1/\sqrt{\ell}$ to $1/\ell$. These results improve our understanding of what is and isn't possible in semi-supervised learning.

Semi-supervised clustering for de-duplication

Data de-duplication is the task of detecting multiple records that correspond to the same real-world entity in a database. In this work, we view de-duplication as a clustering problem where the goal is to put records corresponding to the same physical entity in the same cluster and putting records corresponding to different physical entities into different clusters. We introduce a framework which we call promise correlation clustering. Given a complete graph $G$ with the edges labelled $0$ and $1$, the goal is to find a clustering that minimizes the number of $0$ edges within a cluster plus the number of $1$ edges across different clusters (or correlation loss). The optimal clustering can also be viewed as a complete graph $G^*$ with edges corresponding to points in the same cluster being labelled $0$ and other edges being labelled $1$. Under the promise that the edge difference between $G$ and $G^*$ is "small", we prove that finding the optimal clustering (or $G^*$) is still NP-Hard. [Ashtiani et. al, 2016] introduced the framework of semi-supervised clustering, where the learning algorithm has access to an oracle, which answers whether two points belong to the same or different clusters. We further prove that even with access to a same-cluster oracle, the promise version is NP-Hard as long as the number queries to the oracle is not too large ($o(n)$ where $n$ is the number of vertices). Given these negative results, we consider a restricted version of correlation clustering. As before, the goal is to find a clustering that minimizes the correlation loss. However, we restrict ourselves to a given class $\mathcal F$ of clusterings. We offer a semi-supervised algorithmic approach to solve the restricted variant with success guarantees.

Provably noise-robust, regularised $k$-means clustering

We consider the problem of clustering in the presence of noise. That is, when on top of cluster structure, the data also contains a subset of \emph{unstructured} points. Our goal is to detect the clusters despite the presence of many unstructured points. Any algorithm that achieves this goal is noise-robust. We consider a regularisation method which converts any center-based clustering objective into a noise-robust one. We focus on the $k$-means objective and we prove that the regularised version of $k$-means is NP-Hard even for $k=1$. We consider two algorithms based on the convex (sdp and lp) relaxation of the regularised objective and prove robustness guarantees for both. The sdp and lp relaxation of the standard (non-regularised) $k$-means objective has been previously studied by [ABC+15]. Under the stochastic ball model of the data they show that the sdp-based algorithm recovers the underlying structure as long as the balls are separated by $\delta > 2\sqrt{2} + \epsilon$. We improve upon this result in two ways. First, we show recovery even for $\delta > 2 + \epsilon$. Second, our regularised algorithm recovers the balls even in the presence of noise so long as the number of noisy points is not too large. We complement our theoretical analysis with simulations and analyse the effect of various parameters like regularization constant, noise-level etc. on the performance of our algorithm. In the presence of noise, our algorithm performs better than $k$-means++ on MNIST.

Empirical Risk Minimization under Fairness Constraints

We address the problem of algorithmic fairness: ensuring that sensitive variables do not unfairly influence the outcome of a classifier. We present an approach based on empirical risk minimization, which incorporates a fairness constraint into the learning problem. It encourages the conditional risk of the learned classifier to be approximately constant with respect to the sensitive variable. We derive both risk and fairness bounds that support the statistical consistency of our approach. We specify our approach to kernel methods and observe that the fairness requirement implies an orthogonality constraint which can be easily added to these methods. We further observe that for linear models the constraint translates into a simple data preprocessing step. Experiments indicate that the method is empirically effective and performs favorably against state-of-the-art approaches.