Aggregating Data for Optimal and Private Learning

Multiple Instance Regression (MIR) and Learning from Label Proportions (LLP) are learning frameworks arising in many applications, where the training data is partitioned into disjoint sets or bags, and only an aggregate label i.e., bag-label for each bag is available to the learner. In the case of MIR, the bag-label is the label of an undisclosed instance from the bag, while in LLP, the bag-label is the mean of the bag's labels. In this paper, we study for various loss functions in MIR and LLP, what is the optimal way to partition the dataset into bags such that the utility for downstream tasks like linear regression is maximized. We theoretically provide utility guarantees, and show that in each case, the optimal bagging strategy (approximately) reduces to finding an optimal clustering of the feature vectors or the labels with respect to natural objectives such as $k$-means. We also show that our bagging mechanisms can be made label-differentially private, incurring an additional utility error. We then generalize our results to the setting of Generalized Linear Models (GLMs). Finally, we experimentally validate our theoretical results.

On the Power of Randomization in Fair Classification and Representation

Fair classification and fair representation learning are two important problems in supervised and unsupervised fair machine learning, respectively. Fair classification asks for a classifier that maximizes accuracy on a given data distribution subject to fairness constraints. Fair representation maps a given data distribution over the original feature space to a distribution over a new representation space such that all classifiers over the representation satisfy fairness. In this paper, we examine the power of randomization in both these problems to minimize the loss of accuracy that results when we impose fairness constraints. Previous work on fair classification has characterized the optimal fair classifiers on a given data distribution that maximize accuracy subject to fairness constraints, e.g., Demographic Parity (DP), Equal Opportunity (EO), and Predictive Equality (PE). We refine these characterizations to demonstrate when the optimal randomized fair classifiers can surpass their deterministic counterparts in accuracy. We also show how the optimal randomized fair classifier that we characterize can be obtained as a solution to a convex optimization problem. Recent work has provided techniques to construct fair representations for a given data distribution such that any classifier over this representation satisfies DP. However, the classifiers on these fair representations either come with no or weak accuracy guarantees when compared to the optimal fair classifier on the original data distribution. Extending our ideas for randomized fair classification, we improve on these works, and construct DP-fair, EO-fair, and PE-fair representations that have provably optimal accuracy and suffer no accuracy loss compared to the optimal DP-fair, EO-fair, and PE-fair classifiers respectively on the original data distribution.

Private Mean Estimation with Person-Level Differential Privacy

We study differentially private (DP) mean estimation in the case where each person holds multiple samples. Commonly referred to as the "user-level" setting, DP here requires the usual notion of distributional stability when all of a person's datapoints can be modified. Informally, if $n$ people each have $m$ samples from an unknown $d$-dimensional distribution with bounded $k$-th moments, we show that \[n = \tilde \Theta\left(\frac{d}{\alpha^2 m} + \frac{d }{ \alpha m^{1/2} \varepsilon} + \frac{d}{\alpha^{k/(k-1)} m \varepsilon} + \frac{d}{\varepsilon}\right)\] people are necessary and sufficient to estimate the mean up to distance $\alpha$ in $\ell_2$-norm under $\varepsilon$-differential privacy (and its common relaxations). In the multivariate setting, we give computationally efficient algorithms under approximate DP (with slightly degraded sample complexity) and computationally inefficient algorithms under pure DP, and our nearly matching lower bounds hold for the most permissive case of approximate DP. Our computationally efficient estimators are based on the well known noisy-clipped-mean approach, but the analysis for our setting requires new bounds on the tails of sums of independent, vector-valued, bounded-moments random variables, and a new argument for bounding the bias introduced by clipping.

Impossibility results for fair representations

With the growing awareness to fairness in machine learning and the realization of the central role that data representation has in data processing tasks, there is an obvious interest in notions of fair data representations. The goal of such representations is that a model trained on data under the representation (e.g., a classifier) will be guaranteed to respect some fairness constraints. Such representations are useful when they can be fixed for training models on various different tasks and also when they serve as data filtering between the raw data (known to the representation designer) and potentially malicious agents that use the data under the representation to learn predictive models and make decisions. A long list of recent research papers strive to provide tools for achieving these goals. However, we prove that this is basically a futile effort. Roughly stated, we prove that no representation can guarantee the fairness of classifiers for different tasks trained using it; even the basic goal of achieving label-independent Demographic Parity fairness fails once the marginal data distribution shifts. More refined notions of fairness, like Odds Equality, cannot be guaranteed by a representation that does not take into account the task specific labeling rule with respect to which such fairness will be evaluated (even if the marginal data distribution is known a priory). Furthermore, except for trivial cases, no representation can guarantee Odds Equality fairness for any two different tasks, while allowing accurate label predictions for both. While some of our conclusions are intuitive, we formulate (and prove) crisp statements of such impossibilities, often contrasting impressions conveyed by many recent works on fair representations.

Towards the Unification and Robustness of Perturbation and Gradient Based Explanations

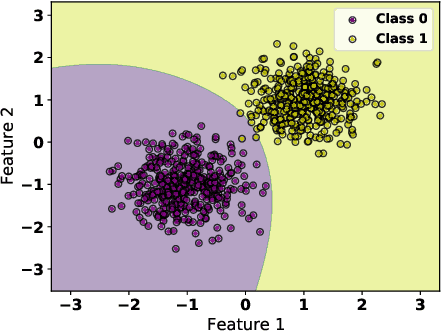
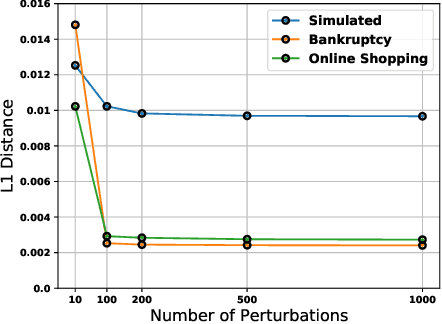
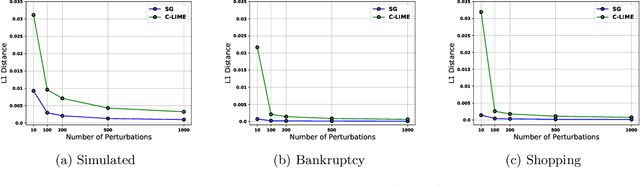
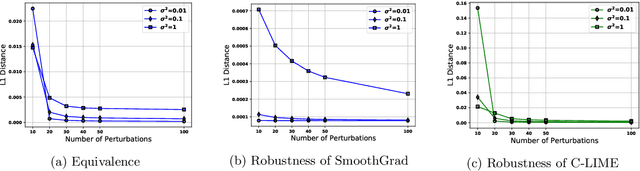
As machine learning black boxes are increasingly being deployed in critical domains such as healthcare and criminal justice, there has been a growing emphasis on developing techniques for explaining these black boxes in a post hoc manner. In this work, we analyze two popular post hoc interpretation techniques: SmoothGrad which is a gradient based method, and a variant of LIME which is a perturbation based method. More specifically, we derive explicit closed form expressions for the explanations output by these two methods and show that they both converge to the same explanation in expectation, i.e., when the number of perturbed samples used by these methods is large. We then leverage this connection to establish other desirable properties, such as robustness, for these techniques. We also derive finite sample complexity bounds for the number of perturbations required for these methods to converge to their expected explanation. Finally, we empirically validate our theory using extensive experimentation on both synthetic and real world datasets.