Aggregating Data for Optimal and Private Learning

Multiple Instance Regression (MIR) and Learning from Label Proportions (LLP) are learning frameworks arising in many applications, where the training data is partitioned into disjoint sets or bags, and only an aggregate label i.e., bag-label for each bag is available to the learner. In the case of MIR, the bag-label is the label of an undisclosed instance from the bag, while in LLP, the bag-label is the mean of the bag's labels. In this paper, we study for various loss functions in MIR and LLP, what is the optimal way to partition the dataset into bags such that the utility for downstream tasks like linear regression is maximized. We theoretically provide utility guarantees, and show that in each case, the optimal bagging strategy (approximately) reduces to finding an optimal clustering of the feature vectors or the labels with respect to natural objectives such as $k$-means. We also show that our bagging mechanisms can be made label-differentially private, incurring an additional utility error. We then generalize our results to the setting of Generalized Linear Models (GLMs). Finally, we experimentally validate our theoretical results.

Learning from Label Proportions and Covariate-shifted Instances

In many applications, especially due to lack of supervision or privacy concerns, the training data is grouped into bags of instances (feature-vectors) and for each bag we have only an aggregate label derived from the instance-labels in the bag. In learning from label proportions (LLP) the aggregate label is the average of the instance-labels in a bag, and a significant body of work has focused on training models in the LLP setting to predict instance-labels. In practice however, the training data may have fully supervised albeit covariate-shifted source data, along with the usual target data with bag-labels, and we wish to train a good instance-level predictor on the target domain. We call this the covariate-shifted hybrid LLP problem. Fully supervised covariate shifted data often has useful training signals and the goal is to leverage them for better predictive performance in the hybrid LLP setting. To achieve this, we develop methods for hybrid LLP which naturally incorporate the target bag-labels along with the source instance-labels, in the domain adaptation framework. Apart from proving theoretical guarantees bounding the target generalization error, we also conduct experiments on several publicly available datasets showing that our methods outperform LLP and domain adaptation baselines as well techniques from previous related work.

Weak to Strong Learning from Aggregate Labels

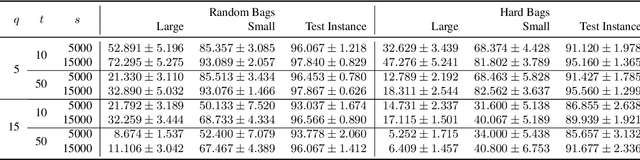
In learning from aggregate labels, the training data consists of sets or "bags" of feature-vectors (instances) along with an aggregate label for each bag derived from the (usually {0,1}-valued) labels of its instances. In learning from label proportions (LLP), the aggregate label is the average of the bag's instance labels, whereas in multiple instance learning (MIL) it is the OR. The goal is to train an instance-level predictor, typically achieved by fitting a model on the training data, in particular one that maximizes the accuracy which is the fraction of satisfied bags i.e., those on which the predicted labels are consistent with the aggregate label. A weak learner has at a constant accuracy < 1 on the training bags, while a strong learner's accuracy can be arbitrarily close to 1. We study the problem of using a weak learner on such training bags with aggregate labels to obtain a strong learner, analogous to supervised learning for which boosting algorithms are known. Our first result shows the impossibility of boosting in LLP using weak classifiers of any accuracy < 1 by constructing a collection of bags for which such weak learners (for any weight assignment) exist, while not admitting any strong learner. A variant of this construction also rules out boosting in MIL for a non-trivial range of weak learner accuracy. In the LLP setting however, we show that a weak learner (with small accuracy) on large enough bags can in fact be used to obtain a strong learner for small bags, in polynomial time. We also provide more efficient, sampling based variant of our procedure with probabilistic guarantees which are empirically validated on three real and two synthetic datasets. Our work is the first to theoretically study weak to strong learning from aggregate labels, with an algorithm to achieve the same for LLP, while proving the impossibility of boosting for both LLP and MIL.

FRACTAL: Fine-Grained Scoring from Aggregate Text Labels

Large language models (LLMs) are being increasingly tuned to power complex generation tasks such as writing, fact-seeking, querying and reasoning. Traditionally, human or model feedback for evaluating and further tuning LLM performance has been provided at the response level, enabling faster and more cost-effective assessments. However, recent works (Amplayo et al. [2022], Wu et al. [2023]) indicate that sentence-level labels may provide more accurate and interpretable feedback for LLM optimization. In this work, we introduce methods to disaggregate response-level labels into sentence-level (pseudo-)labels. Our approach leverages multiple instance learning (MIL) and learning from label proportions (LLP) techniques in conjunction with prior information (e.g., document-sentence cosine similarity) to train a specialized model for sentence-level scoring. We also employ techniques which use model predictions to pseudo-label the train-set at the sentence-level for model training to further improve performance. We conduct extensive evaluations of our methods across six datasets and four tasks: retrieval, question answering, summarization, and math reasoning. Our results demonstrate improved performance compared to multiple baselines across most of these tasks. Our work is the first to develop response-level feedback to sentence-level scoring techniques, leveraging sentence-level prior information, along with comprehensive evaluations on multiple tasks as well as end-to-end finetuning evaluation showing performance comparable to a model trained on fine-grained human annotated labels.

Hardness of Learning Boolean Functions from Label Proportions

In recent years the framework of learning from label proportions (LLP) has been gaining importance in machine learning. In this setting, the training examples are aggregated into subsets or bags and only the average label per bag is available for learning an example-level predictor. This generalizes traditional PAC learning which is the special case of unit-sized bags. The computational learning aspects of LLP were studied in recent works (Saket, NeurIPS'21; Saket, NeurIPS'22) which showed algorithms and hardness for learning halfspaces in the LLP setting. In this work we focus on the intractability of LLP learning Boolean functions. Our first result shows that given a collection of bags of size at most $2$ which are consistent with an OR function, it is NP-hard to find a CNF of constantly many clauses which satisfies any constant-fraction of the bags. This is in contrast with the work of (Saket, NeurIPS'21) which gave a $(2/5)$-approximation for learning ORs using a halfspace. Thus, our result provides a separation between constant clause CNFs and halfspaces as hypotheses for LLP learning ORs. Next, we prove the hardness of satisfying more than $1/2 + o(1)$ fraction of such bags using a $t$-DNF (i.e. DNF where each term has $\leq t$ literals) for any constant $t$. In usual PAC learning such a hardness was known (Khot-Saket, FOCS'08) only for learning noisy ORs. We also study the learnability of parities and show that it is NP-hard to satisfy more than $(q/2^{q-1} + o(1))$-fraction of $q$-sized bags which are consistent with a parity using a parity, while a random parity based algorithm achieves a $(1/2^{q-2})$-approximation.

Label Differential Privacy via Aggregation

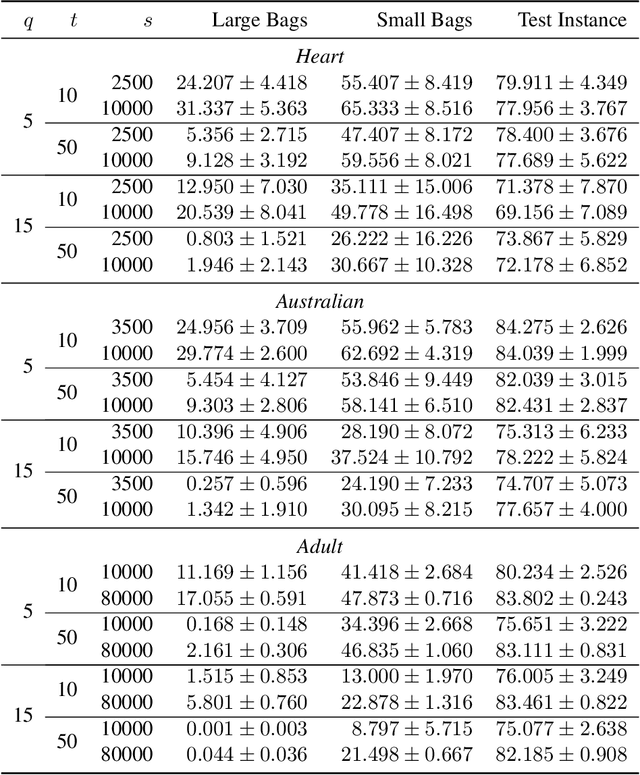
In many real-world applications, in particular due to recent developments in the privacy landscape, training data may be aggregated to preserve the privacy of sensitive training labels. In the learning from label proportions (LLP) framework, the dataset is partitioned into bags of feature-vectors which are available only with the sum of the labels per bag. A further restriction, which we call learning from bag aggregates (LBA) is where instead of individual feature-vectors, only the (possibly weighted) sum of the feature-vectors per bag is available. We study whether such aggregation techniques can provide privacy guarantees under the notion of label differential privacy (label-DP) previously studied in for e.g. [Chaudhuri-Hsu'11, Ghazi et al.'21, Esfandiari et al.'22]. It is easily seen that naive LBA and LLP do not provide label-DP. Our main result however, shows that weighted LBA using iid Gaussian weights with $m$ randomly sampled disjoint $k$-sized bags is in fact $(\varepsilon, \delta)$-label-DP for any $\varepsilon > 0$ with $\delta \approx \exp(-\Omega(\sqrt{k}))$ assuming a lower bound on the linear-mse regression loss. Further, this preserves the optimum over linear mse-regressors of bounded norm to within $(1 \pm o(1))$-factor w.p. $\approx 1 - \exp(-\Omega(m))$. We emphasize that no additive label noise is required. The analogous weighted-LLP does not however admit label-DP. Nevertheless, we show that if additive $N(0, 1)$ noise can be added to any constant fraction of the instance labels, then the noisy weighted-LLP admits similar label-DP guarantees without assumptions on the dataset, while preserving the utility of Lipschitz-bounded neural mse-regression tasks. Our work is the first to demonstrate that label-DP can be achieved by randomly weighted aggregation for regression tasks, using no or little additive noise.

LLP-Bench: A Large Scale Tabular Benchmark for Learning from Label Proportions

In the task of Learning from Label Proportions (LLP), a model is trained on groups (a.k.a bags) of instances and their corresponding label proportions to predict labels for individual instances. LLP has been applied pre-dominantly on two types of datasets - image and tabular. In image LLP, bags of fixed size are created by randomly sampling instances from an underlying dataset. Bags created via this methodology are called random bags. Experimentation on Image LLP has been mostly on random bags on CIFAR-* and MNIST datasets. Despite being a very crucial task in privacy sensitive applications, tabular LLP does not yet have a open, large scale LLP benchmark. One of the unique properties of tabular LLP is the ability to create feature bags where all the instances in a bag have the same value for a given feature. It has been shown in prior research that feature bags are very common in practical, real world applications [Chen et. al '23, Saket et. al. '22]. In this paper, we address the lack of a open, large scale tabular benchmark. First we propose LLP-Bench, a suite of 56 LLP datasets (52 feature bag and 4 random bag datasets) created from the Criteo CTR prediction dataset consisting of 45 million instances. The 56 datasets represent diverse ways in which bags can be constructed from underlying tabular data. To the best of our knowledge, LLP-Bench is the first large scale tabular LLP benchmark with an extensive diversity in constituent datasets. Second, we propose four metrics that characterize and quantify the hardness of a LLP dataset. Using these four metrics we present deep analysis of the 56 datasets in LLP-Bench. Finally we present the performance of 9 SOTA and popular tabular LLP techniques on all the 56 datasets. To the best of our knowledge, our study consisting of more than 2500 experiments is the most extensive study of popular tabular LLP techniques in literature.

PAC Learning Linear Thresholds from Label Proportions

Learning from label proportions (LLP) is a generalization of supervised learning in which the training data is available as sets or bags of feature-vectors (instances) along with the average instance-label of each bag. The goal is to train a good instance classifier. While most previous works on LLP have focused on training models on such training data, computational learnability of LLP was only recently explored by [Saket'21, Saket'22] who showed worst case intractability of properly learning linear threshold functions (LTFs) from label proportions. However, their work did not rule out efficient algorithms for this problem on natural distributions. In this work we show that it is indeed possible to efficiently learn LTFs using LTFs when given access to random bags of some label proportion in which feature-vectors are, conditioned on their labels, independently sampled from a Gaussian distribution $N(\mathbf{\mu}, \mathbf{\Sigma})$. Our work shows that a certain matrix -- formed using covariances of the differences of feature-vectors sampled from the bags with and without replacement -- necessarily has its principal component, after a transformation, in the direction of the normal vector of the LTF. Our algorithm estimates the means and covariance matrices using subgaussian concentration bounds which we show can be applied to efficiently sample bags for approximating the normal direction. Using this in conjunction with novel generalization error bounds in the bag setting, we show that a low error hypothesis LTF can be identified. For some special cases of the $N(\mathbf{0}, \mathbf{I})$ distribution we provide a simpler mean estimation based algorithm. We include an experimental evaluation of our learning algorithms along with a comparison with those of [Saket'21, Saket'22] and random LTFs, demonstrating the effectiveness of our techniques.

Multi-Variate Time Series Forecasting on Variable Subsets

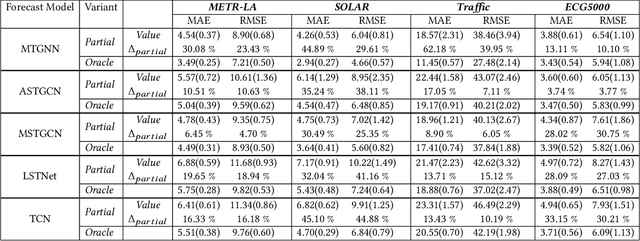
We formulate a new inference task in the domain of multivariate time series forecasting (MTSF), called Variable Subset Forecast (VSF), where only a small subset of the variables is available during inference. Variables are absent during inference because of long-term data loss (eg. sensor failures) or high -> low-resource domain shift between train / test. To the best of our knowledge, robustness of MTSF models in presence of such failures, has not been studied in the literature. Through extensive evaluation, we first show that the performance of state of the art methods degrade significantly in the VSF setting. We propose a non-parametric, wrapper technique that can be applied on top any existing forecast models. Through systematic experiments across 4 datasets and 5 forecast models, we show that our technique is able to recover close to 95\% performance of the models even when only 15\% of the original variables are present.