Towards the Unification and Robustness of Perturbation and Gradient Based Explanations
Paper and Code
Feb 21, 2021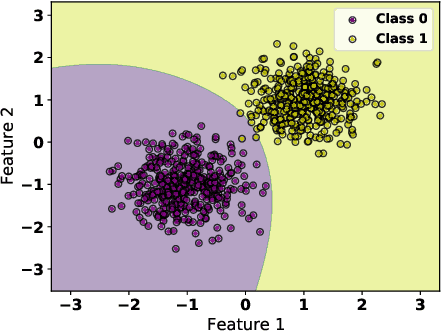
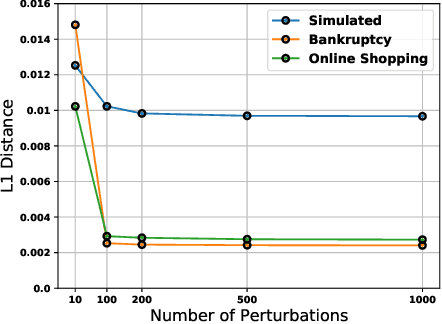
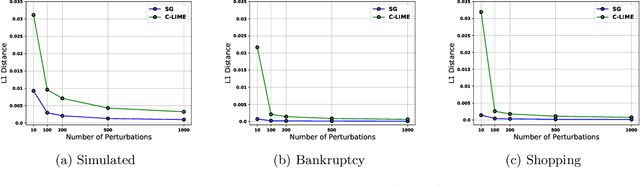
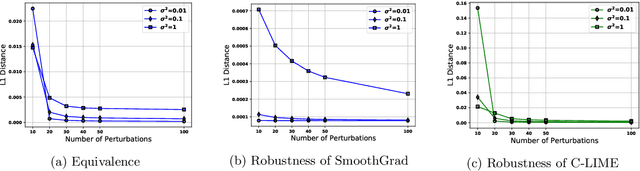
As machine learning black boxes are increasingly being deployed in critical domains such as healthcare and criminal justice, there has been a growing emphasis on developing techniques for explaining these black boxes in a post hoc manner. In this work, we analyze two popular post hoc interpretation techniques: SmoothGrad which is a gradient based method, and a variant of LIME which is a perturbation based method. More specifically, we derive explicit closed form expressions for the explanations output by these two methods and show that they both converge to the same explanation in expectation, i.e., when the number of perturbed samples used by these methods is large. We then leverage this connection to establish other desirable properties, such as robustness, for these techniques. We also derive finite sample complexity bounds for the number of perturbations required for these methods to converge to their expected explanation. Finally, we empirically validate our theory using extensive experimentation on both synthetic and real world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge