Over-parameterization and Adversarial Robustness in Neural Networks: An Overview and Empirical Analysis

Thanks to their extensive capacity, over-parameterized neural networks exhibit superior predictive capabilities and generalization. However, having a large parameter space is considered one of the main suspects of the neural networks' vulnerability to adversarial example -- input samples crafted ad-hoc to induce a desired misclassification. Relevant literature has claimed contradictory remarks in support of and against the robustness of over-parameterized networks. These contradictory findings might be due to the failure of the attack employed to evaluate the networks' robustness. Previous research has demonstrated that depending on the considered model, the algorithm employed to generate adversarial examples may not function properly, leading to overestimating the model's robustness. In this work, we empirically study the robustness of over-parameterized networks against adversarial examples. However, unlike the previous works, we also evaluate the considered attack's reliability to support the results' veracity. Our results show that over-parameterized networks are robust against adversarial attacks as opposed to their under-parameterized counterparts.

Robustness-Congruent Adversarial Training for Secure Machine Learning Model Updates

Machine-learning models demand for periodic updates to improve their average accuracy, exploiting novel architectures and additional data. However, a newly-updated model may commit mistakes that the previous model did not make. Such misclassifications are referred to as negative flips, and experienced by users as a regression of performance. In this work, we show that this problem also affects robustness to adversarial examples, thereby hindering the development of secure model update practices. In particular, when updating a model to improve its adversarial robustness, some previously-ineffective adversarial examples may become misclassified, causing a regression in the perceived security of the system. We propose a novel technique, named robustness-congruent adversarial training, to address this issue. It amounts to fine-tuning a model with adversarial training, while constraining it to retain higher robustness on the adversarial examples that were correctly classified before the update. We show that our algorithm and, more generally, learning with non-regression constraints, provides a theoretically-grounded framework to train consistent estimators. Our experiments on robust models for computer vision confirm that (i) both accuracy and robustness, even if improved after model update, can be affected by negative flips, and (ii) our robustness-congruent adversarial training can mitigate the problem, outperforming competing baseline methods.

Fairness in Machine Learning

Machine learning based systems are reaching society at large and in many aspects of everyday life. This phenomenon has been accompanied by concerns about the ethical issues that may arise from the adoption of these technologies. ML fairness is a recently established area of machine learning that studies how to ensure that biases in the data and model inaccuracies do not lead to models that treat individuals unfavorably on the basis of characteristics such as e.g. race, gender, disabilities, and sexual or political orientation. In this manuscript, we discuss some of the limitations present in the current reasoning about fairness and in methods that deal with it, and describe some work done by the authors to address them. More specifically, we show how causal Bayesian networks can play an important role to reason about and deal with fairness, especially in complex unfairness scenarios. We describe how optimal transport theory can be used to develop methods that impose constraints on the full shapes of distributions corresponding to different sensitive attributes, overcoming the limitation of most approaches that approximate fairness desiderata by imposing constraints on the lower order moments or other functions of those distributions. We present a unified framework that encompasses methods that can deal with different settings and fairness criteria, and that enjoys strong theoretical guarantees. We introduce an approach to learn fair representations that can generalize to unseen tasks. Finally, we describe a technique that accounts for legal restrictions about the use of sensitive attributes.

Fair Regression with Wasserstein Barycenters

We study the problem of learning a real-valued function that satisfies the Demographic Parity constraint. It demands the distribution of the predicted output to be independent of the sensitive attribute. We consider the case that the sensitive attribute is available for prediction. We establish a connection between fair regression and optimal transport theory, based on which we derive a close form expression for the optimal fair predictor. Specifically, we show that the distribution of this optimum is the Wasserstein barycenter of the distributions induced by the standard regression function on the sensitive groups. This result offers an intuitive interpretation of the optimal fair prediction and suggests a simple post-processing algorithm to achieve fairness. We establish risk and distribution-free fairness guarantees for this procedure. Numerical experiments indicate that our method is very effective in learning fair models, with a relative increase in error rate that is inferior to the relative gain in fairness.

Learning Fair and Transferable Representations

Developing learning methods which do not discriminate subgroups in the population is a central goal of algorithmic fairness. One way to reach this goal is by modifying the data representation in order to meet certain fairness constraints. In this work we measure fairness according to demographic parity. This requires the probability of the possible model decisions to be independent of the sensitive information. We argue that the goal of imposing demographic parity can be substantially facilitated within a multitask learning setting. We leverage task similarities by encouraging a shared fair representation across the tasks via low rank matrix factorization. We derive learning bounds establishing that the learned representation transfers well to novel tasks both in terms of prediction performance and fairness metrics. We present experiments on three real world datasets, showing that the proposed method outperforms state-of-the-art approaches by a significant margin.

Leveraging Labeled and Unlabeled Data for Consistent Fair Binary Classification

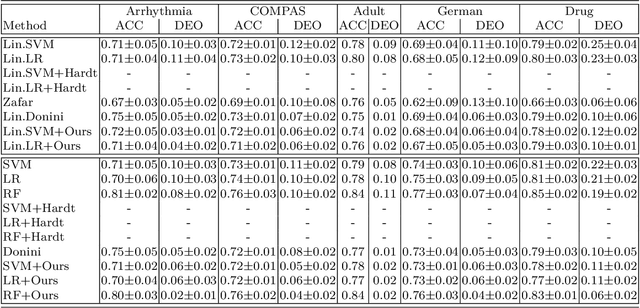
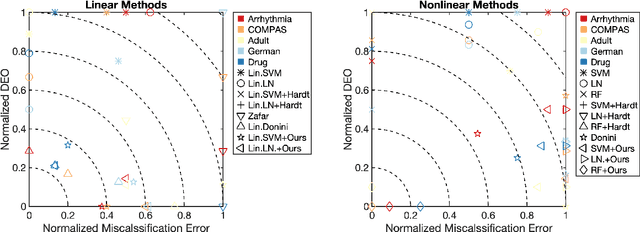
We study the problem of fair binary classification using the notion of Equal Opportunity. It requires the true positive rate to distribute equally across the sensitive groups. Within this setting we show that the fair optimal classifier is obtained by recalibrating the Bayes classifier by a group-dependent threshold. We provide a constructive expression for the threshold. This result motivates us to devise a plug-in classification procedure based on both unlabeled and labeled datasets. While the latter is used to learn the output conditional probability, the former is used for calibration. The overall procedure can be computed in polynomial time and it is shown to be statistically consistent both in terms of classification error and fairness measure. Finally, we present numerical experiments which indicate that our method is often superior or competitive with the state-of-the-art methods on benchmark datasets.

General Fair Empirical Risk Minimization

We tackle the problem of algorithmic fairness, where the goal is to avoid the unfairly influence of sensitive information, in the general context of regression with possible continuous sensitive attributes. We extend the framework of fair empirical risk minimization to this general scenario, covering in this way the whole standard supervised learning setting. Our generalized fairness measure reduces to well known notions of fairness available in literature. We derive learning guarantees for our method, that imply in particular its statistical consistency, both in terms of the risk and the fairness measure. We then specialize our approach to kernel methods and propose a convex fair estimator in that setting. We test the estimator on a commonly used benchmark dataset (Communities and Crime) and on a new dataset collected at the University of Genova, containing the information of the academic career of five thousand students. The latter dataset provides a challenging real case scenario of unfair behaviour of standard regression methods that benefits from our methodology. The experimental results show that our estimator is effective at mitigating the trade-off between accuracy and fairness requirements.

Taking Advantage of Multitask Learning for Fair Classification

A central goal of algorithmic fairness is to reduce bias in automated decision making. An unavoidable tension exists between accuracy gains obtained by using sensitive information (e.g., gender or ethnic group) as part of a statistical model, and any commitment to protect these characteristics. Often, due to biases present in the data, using the sensitive information in the functional form of a classifier improves classification accuracy. In this paper we show how it is possible to get the best of both worlds: optimize model accuracy and fairness without explicitly using the sensitive feature in the functional form of the model, thereby treating different individuals equally. Our method is based on two key ideas. On the one hand, we propose to use Multitask Learning (MTL), enhanced with fairness constraints, to jointly learn group specific classifiers that leverage information between sensitive groups. On the other hand, since learning group specific models might not be permitted, we propose to first predict the sensitive features by any learning method and then to use the predicted sensitive feature to train MTL with fairness constraints. This enables us to tackle fairness with a three-pronged approach, that is, by increasing accuracy on each group, enforcing measures of fairness during training, and protecting sensitive information during testing. Experimental results on two real datasets support our proposal, showing substantial improvements in both accuracy and fairness.

Empirical Risk Minimization under Fairness Constraints

We address the problem of algorithmic fairness: ensuring that sensitive variables do not unfairly influence the outcome of a classifier. We present an approach based on empirical risk minimization, which incorporates a fairness constraint into the learning problem. It encourages the conditional risk of the learned classifier to be approximately constant with respect to the sensitive variable. We derive both risk and fairness bounds that support the statistical consistency of our approach. We specify our approach to kernel methods and observe that the fairness requirement implies an orthogonality constraint which can be easily added to these methods. We further observe that for linear models the constraint translates into a simple data preprocessing step. Experiments indicate that the method is empirically effective and performs favorably against state-of-the-art approaches.