Regression under demographic parity constraints via unlabeled post-processing

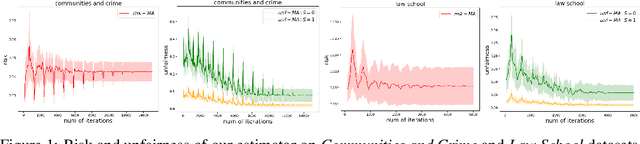
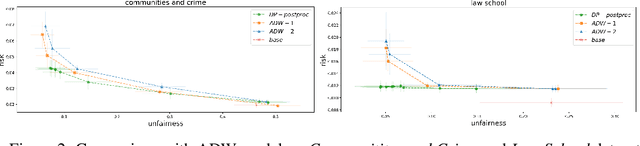
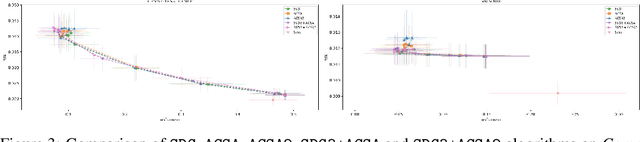
We address the problem of performing regression while ensuring demographic parity, even without access to sensitive attributes during inference. We present a general-purpose post-processing algorithm that, using accurate estimates of the regression function and a sensitive attribute predictor, generates predictions that meet the demographic parity constraint. Our method involves discretization and stochastic minimization of a smooth convex function. It is suitable for online post-processing and multi-class classification tasks only involving unlabeled data for the post-processing. Unlike prior methods, our approach is fully theory-driven. We require precise control over the gradient norm of the convex function, and thus, we rely on more advanced techniques than standard stochastic gradient descent. Our algorithm is backed by finite-sample analysis and post-processing bounds, with experimental results validating our theoretical findings.

Narrowing the Gap between Adversarial and Stochastic MDPs via Policy Optimization

In this paper, we consider the problem of learning in adversarial Markov decision processes [MDPs] with an oblivious adversary in a full-information setting. The agent interacts with an environment during $T$ episodes, each of which consists of $H$ stages, and each episode is evaluated with respect to a reward function that will be revealed only at the end of the episode. We propose an algorithm, called APO-MVP, that achieves a regret bound of order $\tilde{\mathcal{O}}(\mathrm{poly}(H)\sqrt{SAT})$, where $S$ and $A$ are sizes of the state and action spaces, respectively. This result improves upon the best-known regret bound by a factor of $\sqrt{S}$, bridging the gap between adversarial and stochastic MDPs, and matching the minimax lower bound $\Omega(\sqrt{H^3SAT})$ as far as the dependencies in $S,A,T$ are concerned. The proposed algorithm and analysis completely avoid the typical tool given by occupancy measures; instead, it performs policy optimization based only on dynamic programming and on a black-box online linear optimization strategy run over estimated advantage functions, making it easy to implement. The analysis leverages two recent techniques: policy optimization based on online linear optimization strategies (Jonckheere et al., 2023) and a refined martingale analysis of the impact on values of estimating transitions kernels (Zhang et al., 2023).

Gradient-free optimization of highly smooth functions: improved analysis and a new algorithm

This work studies minimization problems with zero-order noisy oracle information under the assumption that the objective function is highly smooth and possibly satisfies additional properties. We consider two kinds of zero-order projected gradient descent algorithms, which differ in the form of the gradient estimator. The first algorithm uses a gradient estimator based on randomization over the $\ell_2$ sphere due to Bach and Perchet (2016). We present an improved analysis of this algorithm on the class of highly smooth and strongly convex functions studied in the prior work, and we derive rates of convergence for two more general classes of non-convex functions. Namely, we consider highly smooth functions satisfying the Polyak-{\L}ojasiewicz condition and the class of highly smooth functions with no additional property. The second algorithm is based on randomization over the $\ell_1$ sphere, and it extends to the highly smooth setting the algorithm that was recently proposed for Lipschitz convex functions in Akhavan et al. (2022). We show that, in the case of noiseless oracle, this novel algorithm enjoys better bounds on bias and variance than the $\ell_2$ randomization and the commonly used Gaussian randomization algorithms, while in the noisy case both $\ell_1$ and $\ell_2$ algorithms benefit from similar improved theoretical guarantees. The improvements are achieved thanks to a new proof techniques based on Poincar\'e type inequalities for uniform distributions on the $\ell_1$ or $\ell_2$ spheres. The results are established under weak (almost adversarial) assumptions on the noise. Moreover, we provide minimax lower bounds proving optimality or near optimality of the obtained upper bounds in several cases.

Parameter-free projected gradient descent

We consider the problem of minimizing a convex function over a closed convex set, with Projected Gradient Descent (PGD). We propose a fully parameter-free version of AdaGrad, which is adaptive to the distance between the initialization and the optimum, and to the sum of the square norm of the subgradients. Our algorithm is able to handle projection steps, does not involve restarts, reweighing along the trajectory or additional gradient evaluations compared to the classical PGD. It also fulfills optimal rates of convergence for cumulative regret up to logarithmic factors. We provide an extension of our approach to stochastic optimization and conduct numerical experiments supporting the developed theory.

Small Total-Cost Constraints in Contextual Bandits with Knapsacks, with Application to Fairness

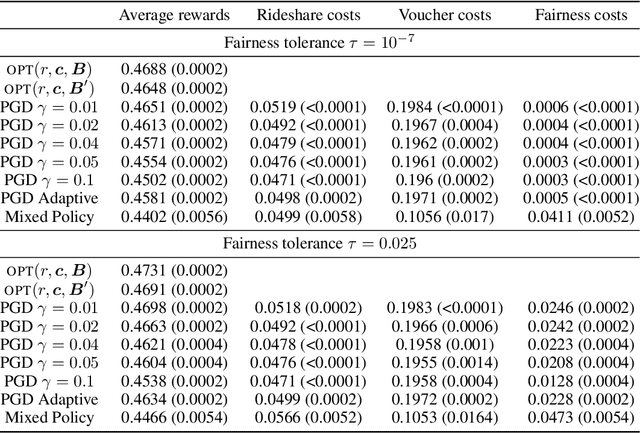
We consider contextual bandit problems with knapsacks [CBwK], a problem where at each round, a scalar reward is obtained and vector-valued costs are suffered. The learner aims to maximize the cumulative rewards while ensuring that the cumulative costs are lower than some predetermined cost constraints. We assume that contexts come from a continuous set, that costs can be signed, and that the expected reward and cost functions, while unknown, may be uniformly estimated -- a typical assumption in the literature. In this setting, total cost constraints had so far to be at least of order $T^{3/4}$, where $T$ is the number of rounds, and were even typically assumed to depend linearly on $T$. We are however motivated to use CBwK to impose a fairness constraint of equalized average costs between groups: the budget associated with the corresponding cost constraints should be as close as possible to the natural deviations, of order $\sqrt{T}$. To that end, we introduce a dual strategy based on projected-gradient-descent updates, that is able to deal with total-cost constraints of the order of $\sqrt{T}$ up to poly-logarithmic terms. This strategy is more direct and simpler than existing strategies in the literature. It relies on a careful, adaptive, tuning of the step size.

SignSVRG: fixing SignSGD via variance reduction

We consider the problem of unconstrained minimization of finite sums of functions. We propose a simple, yet, practical way to incorporate variance reduction techniques into SignSGD, guaranteeing convergence that is similar to the full sign gradient descent. The core idea is first instantiated on the problem of minimizing sums of convex and Lipschitz functions and is then extended to the smooth case via variance reduction. Our analysis is elementary and much simpler than the typical proof for variance reduction methods. We show that for smooth functions our method gives $\mathcal{O}(1 / \sqrt{T})$ rate for expected norm of the gradient and $\mathcal{O}(1/T)$ rate in the case of smooth convex functions, recovering convergence results of deterministic methods, while preserving computational advantages of SignSGD.

A gradient estimator via L1-randomization for online zero-order optimization with two point feedback

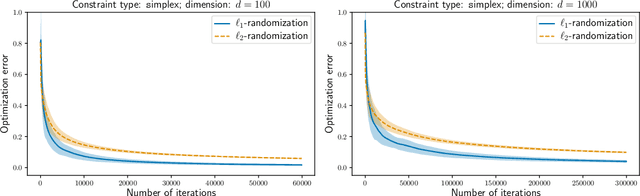
This work studies online zero-order optimization of convex and Lipschitz functions. We present a novel gradient estimator based on two function evaluation and randomization on the $\ell_1$-sphere. Considering different geometries of feasible sets and Lipschitz assumptions we analyse online mirror descent algorithm with our estimator in place of the usual gradient. We consider two types of assumptions on the noise of the zero-order oracle: canceling noise and adversarial noise. We provide an anytime and completely data-driven algorithm, which is adaptive to all parameters of the problem. In the case of canceling noise that was previously studied in the literature, our guarantees are either comparable or better than state-of-the-art bounds obtained by~\citet{duchi2015} and \citet{Shamir17} for non-adaptive algorithms. Our analysis is based on deriving a new Poincar\'e type inequality for the uniform measure on the $\ell_1$-sphere with explicit constants, which may be of independent interest.

A Unified Approach to Fair Online Learning via Blackwell Approachability

We provide a setting and a general approach to fair online learning with stochastic sensitive and non-sensitive contexts. The setting is a repeated game between the Player and Nature, where at each stage both pick actions based on the contexts. Inspired by the notion of unawareness, we assume that the Player can only access the non-sensitive context before making a decision, while we discuss both cases of Nature accessing the sensitive contexts and Nature unaware of the sensitive contexts. Adapting Blackwell's approachability theory to handle the case of an unknown contexts' distribution, we provide a general necessary and sufficient condition for learning objectives to be compatible with some fairness constraints. This condition is instantiated on (group-wise) no-regret and (group-wise) calibration objectives, and on demographic parity as an additional constraint. When the objective is not compatible with the constraint, the provided framework permits to characterise the optimal trade-off between the two.

Set-valued classification -- overview via a unified framework

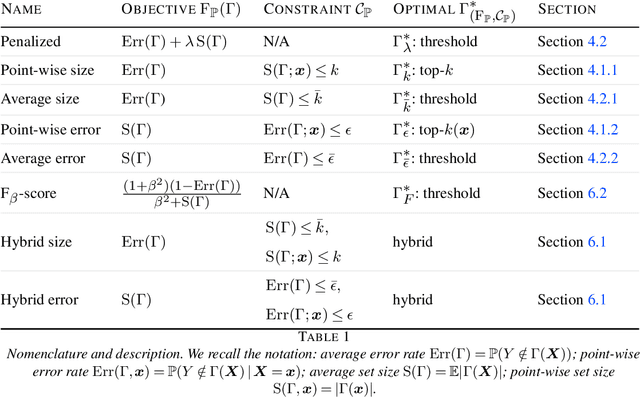
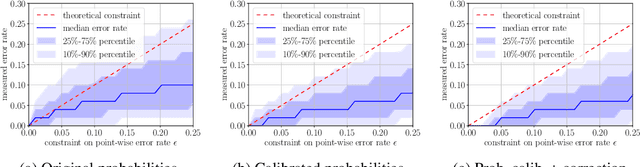
Multi-class classification problem is among the most popular and well-studied statistical frameworks. Modern multi-class datasets can be extremely ambiguous and single-output predictions fail to deliver satisfactory performance. By allowing predictors to predict a set of label candidates, set-valued classification offers a natural way to deal with this ambiguity. Several formulations of set-valued classification are available in the literature and each of them leads to different prediction strategies. The present survey aims to review popular formulations using a unified statistical framework. The proposed framework encompasses previously considered and leads to new formulations as well as it allows to understand underlying trade-offs of each formulation. We provide infinite sample optimal set-valued classification strategies and review a general plug-in principle to construct data-driven algorithms. The exposition is supported by examples and pointers to both theoretical and practical contributions. Finally, we provide experiments on real-world datasets comparing these approaches in practice and providing general practical guidelines.

Classification with abstention but without disparities

Classification with abstention has gained a lot of attention in recent years as it allows to incorporate human decision-makers in the process. Yet, abstention can potentially amplify disparities and lead to discriminatory predictions. The goal of this work is to build a general purpose classification algorithm, which is able to abstain from prediction, while avoiding disparate impact. We formalize this problem as risk minimization under fairness and abstention constraints for which we derive the form of the optimal classifier. Building on this result, we propose a post-processing classification algorithm, which is able to modify any off-the-shelf score-based classifier using only unlabeled sample. We establish finite sample risk, fairness, and abstention guarantees for the proposed algorithm. In particular, it is shown that fairness and abstention constraints can be achieved independently from the initial classifier as long as sufficiently many unlabeled data is available. The risk guarantee is established in terms of the quality of the initial classifier. Our post-processing scheme reduces to a sparse linear program allowing for an efficient implementation, which we provide. Finally, we validate our method empirically showing that moderate abstention rates allow to bypass the risk-fairness trade-off.