Conformal Prediction for Hierarchical Data

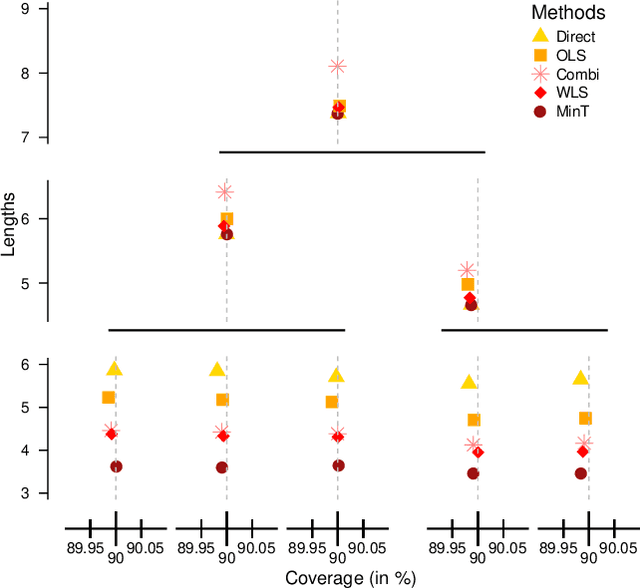
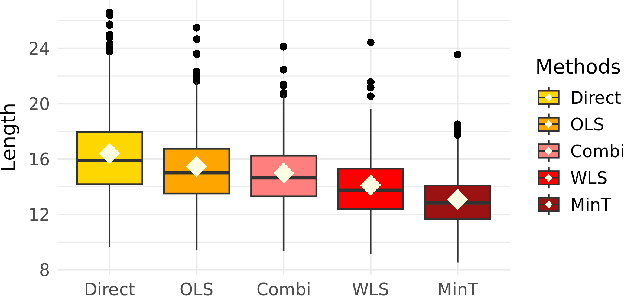
Reconciliation has become an essential tool in multivariate point forecasting for hierarchical time series. However, there is still a lack of understanding of the theoretical properties of probabilistic Forecast Reconciliation techniques. Meanwhile, Conformal Prediction is a general framework with growing appeal that provides prediction sets with probabilistic guarantees in finite sample. In this paper, we propose a first step towards combining Conformal Prediction and Forecast Reconciliation by analyzing how including a reconciliation step in the Split Conformal Prediction (SCP) procedure enhances the resulting prediction sets. In particular, we show that the validity granted by SCP remains while improving the efficiency of the prediction sets. We also advocate a variation of the theoretical procedure for practical use. Finally, we illustrate these results with simulations.

Narrowing the Gap between Adversarial and Stochastic MDPs via Policy Optimization

In this paper, we consider the problem of learning in adversarial Markov decision processes [MDPs] with an oblivious adversary in a full-information setting. The agent interacts with an environment during $T$ episodes, each of which consists of $H$ stages, and each episode is evaluated with respect to a reward function that will be revealed only at the end of the episode. We propose an algorithm, called APO-MVP, that achieves a regret bound of order $\tilde{\mathcal{O}}(\mathrm{poly}(H)\sqrt{SAT})$, where $S$ and $A$ are sizes of the state and action spaces, respectively. This result improves upon the best-known regret bound by a factor of $\sqrt{S}$, bridging the gap between adversarial and stochastic MDPs, and matching the minimax lower bound $\Omega(\sqrt{H^3SAT})$ as far as the dependencies in $S,A,T$ are concerned. The proposed algorithm and analysis completely avoid the typical tool given by occupancy measures; instead, it performs policy optimization based only on dynamic programming and on a black-box online linear optimization strategy run over estimated advantage functions, making it easy to implement. The analysis leverages two recent techniques: policy optimization based on online linear optimization strategies (Jonckheere et al., 2023) and a refined martingale analysis of the impact on values of estimating transitions kernels (Zhang et al., 2023).

Symphony of experts: orchestration with adversarial insights in reinforcement learning

Structured reinforcement learning leverages policies with advantageous properties to reach better performance, particularly in scenarios where exploration poses challenges. We explore this field through the concept of orchestration, where a (small) set of expert policies guides decision-making; the modeling thereof constitutes our first contribution. We then establish value-functions regret bounds for orchestration in the tabular setting by transferring regret-bound results from adversarial settings. We generalize and extend the analysis of natural policy gradient in Agarwal et al. [2021, Section 5.3] to arbitrary adversarial aggregation strategies. We also extend it to the case of estimated advantage functions, providing insights into sample complexity both in expectation and high probability. A key point of our approach lies in its arguably more transparent proofs compared to existing methods. Finally, we present simulations for a stochastic matching toy model.

Parameter-free projected gradient descent

We consider the problem of minimizing a convex function over a closed convex set, with Projected Gradient Descent (PGD). We propose a fully parameter-free version of AdaGrad, which is adaptive to the distance between the initialization and the optimum, and to the sum of the square norm of the subgradients. Our algorithm is able to handle projection steps, does not involve restarts, reweighing along the trajectory or additional gradient evaluations compared to the classical PGD. It also fulfills optimal rates of convergence for cumulative regret up to logarithmic factors. We provide an extension of our approach to stochastic optimization and conduct numerical experiments supporting the developed theory.

Small Total-Cost Constraints in Contextual Bandits with Knapsacks, with Application to Fairness

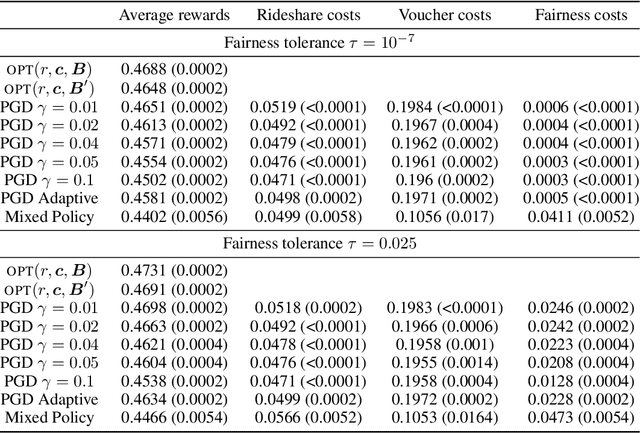
We consider contextual bandit problems with knapsacks [CBwK], a problem where at each round, a scalar reward is obtained and vector-valued costs are suffered. The learner aims to maximize the cumulative rewards while ensuring that the cumulative costs are lower than some predetermined cost constraints. We assume that contexts come from a continuous set, that costs can be signed, and that the expected reward and cost functions, while unknown, may be uniformly estimated -- a typical assumption in the literature. In this setting, total cost constraints had so far to be at least of order $T^{3/4}$, where $T$ is the number of rounds, and were even typically assumed to depend linearly on $T$. We are however motivated to use CBwK to impose a fairness constraint of equalized average costs between groups: the budget associated with the corresponding cost constraints should be as close as possible to the natural deviations, of order $\sqrt{T}$. To that end, we introduce a dual strategy based on projected-gradient-descent updates, that is able to deal with total-cost constraints of the order of $\sqrt{T}$ up to poly-logarithmic terms. This strategy is more direct and simpler than existing strategies in the literature. It relies on a careful, adaptive, tuning of the step size.

On Best-Arm Identification with a Fixed Budget in Non-Parametric Multi-Armed Bandits

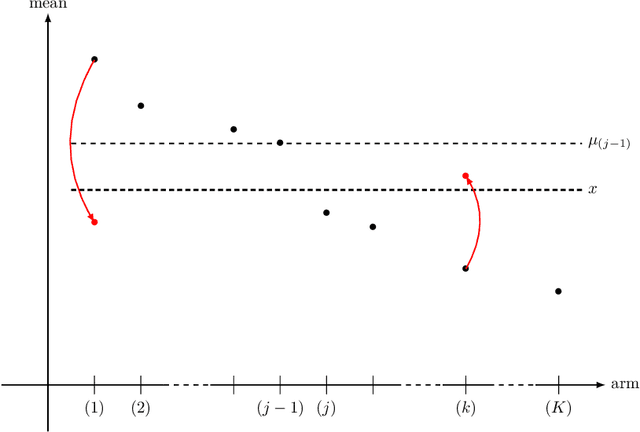
We lay the foundations of a non-parametric theory of best-arm identification in multi-armed bandits with a fixed budget T. We consider general, possibly non-parametric, models D for distributions over the arms; an overarching example is the model D = P(0,1) of all probability distributions over [0,1]. We propose upper bounds on the average log-probability of misidentifying the optimal arm based on information-theoretic quantities that correspond to infima over Kullback-Leibler divergences between some distributions in D and a given distribution. This is made possible by a refined analysis of the successive-rejects strategy of Audibert, Bubeck, and Munos (2010). We finally provide lower bounds on the same average log-probability, also in terms of the same new information-theoretic quantities; these lower bounds are larger when the (natural) assumptions on the considered strategies are stronger. All these new upper and lower bounds generalize existing bounds based, e.g., on gaps between distributions.

Contextual Bandits with Knapsacks for a Conversion Model

We consider contextual bandits with knapsacks, with an underlying structure between rewards generated and cost vectors suffered. We do so motivated by sales with commercial discounts. At each round, given the stochastic i.i.d.\ context $\mathbf{x}_t$ and the arm picked $a_t$ (corresponding, e.g., to a discount level), a customer conversion may be obtained, in which case a reward $r(a,\mathbf{x}_t)$ is gained and vector costs $c(a_t,\mathbf{x}_t)$ are suffered (corresponding, e.g., to losses of earnings). Otherwise, in the absence of a conversion, the reward and costs are null. The reward and costs achieved are thus coupled through the binary variable measuring conversion or the absence thereof. This underlying structure between rewards and costs is different from the linear structures considered by Agrawal and Devanur [2016] but we show that the techniques introduced in this article may also be applied to the latter case. Namely, the adaptive policies exhibited solve at each round a linear program based on upper-confidence estimates of the probabilities of conversion given $a$ and $\mathbf{x}$. This kind of policy is most natural and achieves a regret bound of the typical order (OPT/$B$) $\sqrt{T}$, where $B$ is the total budget allowed, OPT is the optimal expected reward achievable by a static policy, and $T$ is the number of rounds.

A Unified Approach to Fair Online Learning via Blackwell Approachability

We provide a setting and a general approach to fair online learning with stochastic sensitive and non-sensitive contexts. The setting is a repeated game between the Player and Nature, where at each stage both pick actions based on the contexts. Inspired by the notion of unawareness, we assume that the Player can only access the non-sensitive context before making a decision, while we discuss both cases of Nature accessing the sensitive contexts and Nature unaware of the sensitive contexts. Adapting Blackwell's approachability theory to handle the case of an unknown contexts' distribution, we provide a general necessary and sufficient condition for learning objectives to be compatible with some fairness constraints. This condition is instantiated on (group-wise) no-regret and (group-wise) calibration objectives, and on demographic parity as an additional constraint. When the objective is not compatible with the constraint, the provided framework permits to characterise the optimal trade-off between the two.

Diversity-Preserving K-Armed Bandits, Revisited

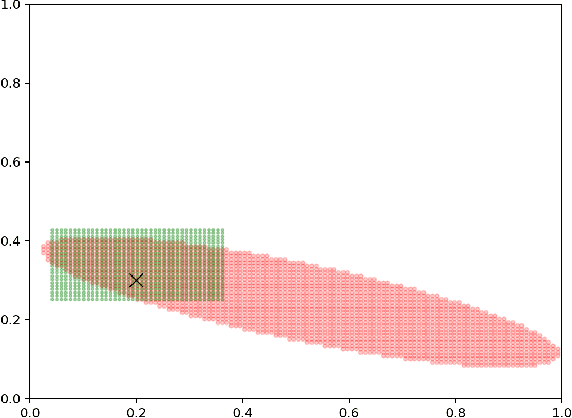
We consider the bandit-based framework for diversity-preserving recommendations introduced by Celis et al. (2019), who approached it mainly by a reduction to the setting of linear bandits. We design a UCB algorithm using the specific structure of the setting and show that it enjoys a bounded distribution-dependent regret in the natural cases when the optimal mixed actions put some probability mass on all actions (i.e., when diversity is desirable). Simulations illustrate this fact. We also provide regret lower bounds and briefly discuss distribution-free regret bounds.

Adaptation to the Range in $K$-Armed Bandits

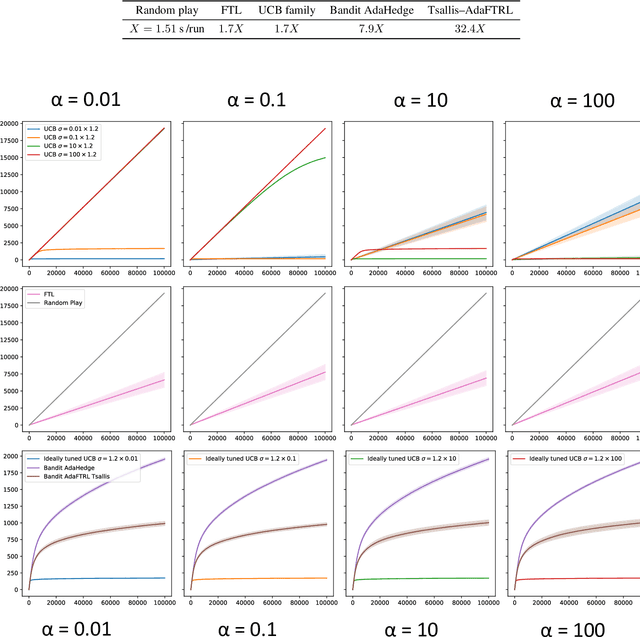
We consider stochastic bandit problems with $K$ arms, each associated with a bounded distribution supported on the range $[m,M]$. We do not assume that the range $[m,M]$ is known and show that there is a cost for learning this range. Indeed, a new trade-off between distribution-dependent and distribution-free regret bounds arises, which, for instance, prevents from simultaneously achieving the typical $\ln T$ and $\sqrt{T}$ bounds. For instance, a $\sqrt{T}$ distribution-free regret bound may only be achieved if the distribution-dependent regret bounds are at least of order $\sqrt{T}$. We exhibit a strategy achieving the rates for regret indicated by the new trade-off.