Tracking solutions of time-varying variational inequalities

Tracking the solution of time-varying variational inequalities is an important problem with applications in game theory, optimization, and machine learning. Existing work considers time-varying games or time-varying optimization problems. For strongly convex optimization problems or strongly monotone games, these results provide tracking guarantees under the assumption that the variation of the time-varying problem is restrained, that is, problems with a sublinear solution path. In this work we extend existing results in two ways: In our first result, we provide tracking bounds for (1) variational inequalities with a sublinear solution path but not necessarily monotone functions, and (2) for periodic time-varying variational inequalities that do not necessarily have a sublinear solution path-length. Our second main contribution is an extensive study of the convergence behavior and trajectory of discrete dynamical systems of periodic time-varying VI. We show that these systems can exhibit provably chaotic behavior or can converge to the solution. Finally, we illustrate our theoretical results with experiments.

Towards Characterizing the First-order Query Complexity of Learning (Approximate) Nash Equilibria in Zero-sum Matrix Games

In the first-order query model for zero-sum $K\times K$ matrix games, playersobserve the expected pay-offs for all their possible actions under therandomized action played by their opponent. This is a classical model,which has received renewed interest after the discoveryby Rakhlin and Sridharan that $\epsilon$-approximate Nash equilibria can be computedefficiently from $O(\ln K / \epsilon) $ instead of $O( \ln K / \epsilon^2)$ queries.Surprisingly, the optimal number of such queries, as a function of both$\epsilon$ and $K$, is not known.We make progress on this question on two fronts. First, we fully characterise the query complexity of learning exact equilibria ($\epsilon=0$), by showing that they require a number of queries that is linearin $K$, which means that it is essentially as hard as querying the wholematrix, which can also be done with $K$ queries. Second, for $\epsilon > 0$, the currentquery complexity upper bound stands at $O(\min(\ln(K) / \epsilon , K))$. We argue that, unfortunately, obtaining matchinglower bound is not possible with existing techniques: we prove that nolower bound can be derived by constructing hard matrices whose entriestake values in a known countable set, because such matrices can be fullyidentified by a single query. This rules out, for instance, reducing toa submodular optimization problem over the hypercube by encoding itas a binary matrix. We then introduce a new technique for lower bounds,which allows us to obtain lower bounds of order$\tilde\Omega(\log(1 / (K\epsilon)))$ for any $\epsilon \leq1 / cK^4$, where $c$ is a constant independent of $K$. We furtherdiscuss possible future directions to improve on our techniques in orderto close the gap with the upper bounds.

Between Stochastic and Adversarial Online Convex Optimization: Improved Regret Bounds via Smoothness

Stochastic and adversarial data are two widely studied settings in online learning. But many optimization tasks are neither i.i.d. nor fully adversarial, which makes it of fundamental interest to get a better theoretical understanding of the world between these extremes. In this work we establish novel regret bounds for online convex optimization in a setting that interpolates between stochastic i.i.d. and fully adversarial losses. By exploiting smoothness of the expected losses, these bounds replace a dependence on the maximum gradient length by the variance of the gradients, which was previously known only for linear losses. In addition, they weaken the i.i.d. assumption by allowing adversarially poisoned rounds or shifts in the data distribution. To accomplish this goal, we introduce two key quantities associated with the loss sequence, that we call the cumulative stochastic variance and the adversarial variation. Our upper bounds are attained by instances of optimistic follow the regularized leader, and we design adaptive learning rates that automatically adapt to the cumulative stochastic variance and adversarial variation. In the fully i.i.d. case, our bounds match the rates one would expect from results in stochastic acceleration, and in the fully adversarial case they gracefully deteriorate to match the minimax regret. We further provide lower bounds showing that our regret upper bounds are tight for all intermediate regimes for the cumulative stochastic variance and the adversarial variation.

Scale-free Unconstrained Online Learning for Curved Losses

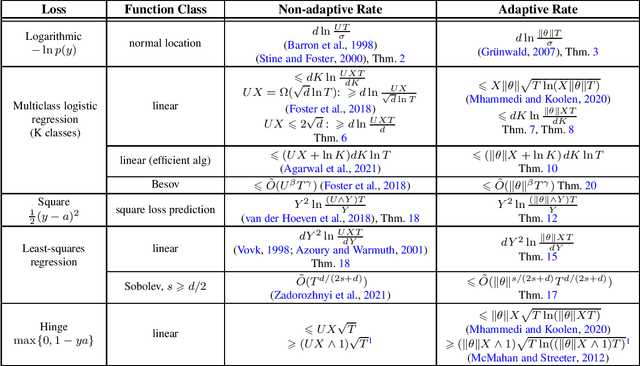
A sequence of works in unconstrained online convex optimisation have investigated the possibility of adapting simultaneously to the norm $U$ of the comparator and the maximum norm $G$ of the gradients. In full generality, matching upper and lower bounds are known which show that this comes at the unavoidable cost of an additive $G U^3$, which is not needed when either $G$ or $U$ is known in advance. Surprisingly, recent results by Kempka et al. (2019) show that no such price for adaptivity is needed in the specific case of $1$-Lipschitz losses like the hinge loss. We follow up on this observation by showing that there is in fact never a price to pay for adaptivity if we specialise to any of the other common supervised online learning losses: our results cover log loss, (linear and non-parametric) logistic regression, square loss prediction, and (linear and non-parametric) least-squares regression. We also fill in several gaps in the literature by providing matching lower bounds with an explicit dependence on $U$. In all cases we obtain scale-free algorithms, which are suitably invariant under rescaling of the data. Our general goal is to establish achievable rates without concern for computational efficiency, but for linear logistic regression we also provide an adaptive method that is as efficient as the recent non-adaptive algorithm by Agarwal et al. (2021).

Distributed Online Learning for Joint Regret with Communication Constraints

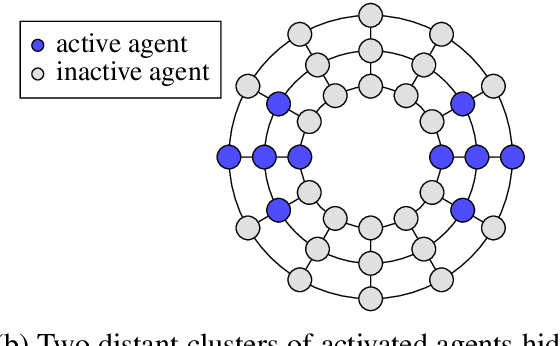
In this paper we consider a distributed online learning setting for joint regret with communication constraints. This is a multi-agent setting in which in each round $t$ an adversary activates an agent, which has to issue a prediction. A subset of all the agents may then communicate a $b$-bit message to their neighbors in a graph. All agents cooperate to control the joint regret, which is the sum of the losses of the agents minus the losses evaluated at the best fixed common comparator parameters $\pmb{u}$. We provide a comparator-adaptive algorithm for this setting, which means that the joint regret scales with the norm of the comparator $\|\pmb{u}\|$. To address communication constraints we provide deterministic and stochastic gradient compression schemes and show that with these compression schemes our algorithm has worst-case optimal regret for the case that all agents communicate in every round. Additionally, we exploit the comparator-adaptive property of our algorithm to learn the best partition from a set of candidate partitions, which allows different subsets of agents to learn a different comparator.

Diversity-Preserving K-Armed Bandits, Revisited

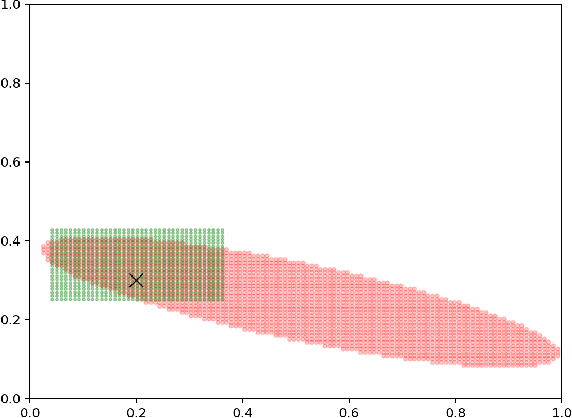
We consider the bandit-based framework for diversity-preserving recommendations introduced by Celis et al. (2019), who approached it mainly by a reduction to the setting of linear bandits. We design a UCB algorithm using the specific structure of the setting and show that it enjoys a bounded distribution-dependent regret in the natural cases when the optimal mixed actions put some probability mass on all actions (i.e., when diversity is desirable). Simulations illustrate this fact. We also provide regret lower bounds and briefly discuss distribution-free regret bounds.

Adaptation to the Range in $K$-Armed Bandits

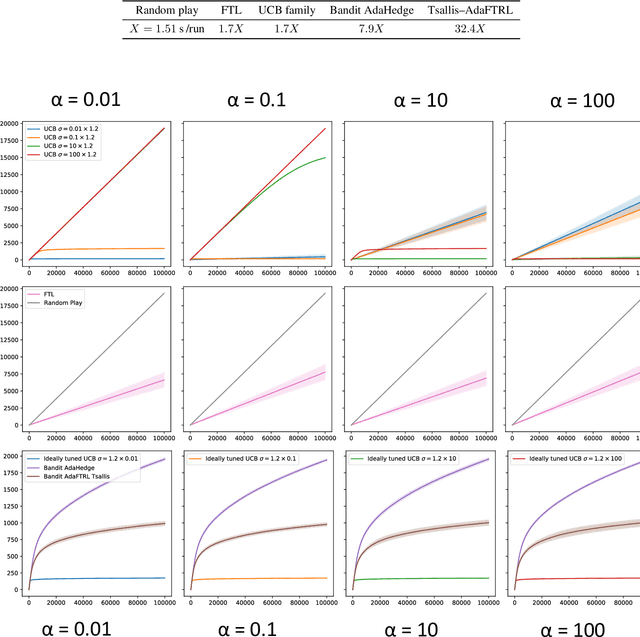
We consider stochastic bandit problems with $K$ arms, each associated with a bounded distribution supported on the range $[m,M]$. We do not assume that the range $[m,M]$ is known and show that there is a cost for learning this range. Indeed, a new trade-off between distribution-dependent and distribution-free regret bounds arises, which, for instance, prevents from simultaneously achieving the typical $\ln T$ and $\sqrt{T}$ bounds. For instance, a $\sqrt{T}$ distribution-free regret bound may only be achieved if the distribution-dependent regret bounds are at least of order $\sqrt{T}$. We exhibit a strategy achieving the rates for regret indicated by the new trade-off.

Polynomial Cost of Adaptation for X -Armed Bandits

In the context of stochastic continuum-armed bandits, we present an algorithm that adapts to the unknown smoothness of the objective function. We exhibit and compute a polynomial cost of adaptation to the H{\"o}lder regularity for regret minimization. To do this, we first reconsider the recent lower bound of Locatelli and Carpentier [20], and define and characterize admissible rate functions. Our new algorithm matches any of these minimal rate functions. We provide a finite-time analysis and a thorough discussion about asymptotic optimality.

KL-UCB-switch: optimal regret bounds for stochastic bandits from both a distribution-dependent and a distribution-free viewpoints

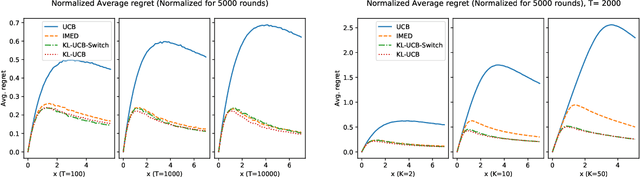
In the context of K-armed stochastic bandits with distribution only assumed to be supported by [0, 1], we introduce a new algorithm, KL-UCB-switch, and prove that it enjoys simultaneously a distribution-free regret bound of optimal order \sqrt{KT} and a distribution-dependent regret bound of optimal order as well, that is, matching the \kappa \ln T lower bound by Lai and Robbins (1985) and Burnetas and Katehakis (1996).