Beyond Average Return in Markov Decision Processes

What are the functionals of the reward that can be computed and optimized exactly in Markov Decision Processes? In the finite-horizon, undiscounted setting, Dynamic Programming (DP) can only handle these operations efficiently for certain classes of statistics. We summarize the characterization of these classes for policy evaluation, and give a new answer for the planning problem. Interestingly, we prove that only generalized means can be optimized exactly, even in the more general framework of Distributional Reinforcement Learning (DistRL).DistRL permits, however, to evaluate other functionals approximately. We provide error bounds on the resulting estimators, and discuss the potential of this approach as well as its limitations.These results contribute to advancing the theory of Markov Decision Processes by examining overall characteristics of the return, and particularly risk-conscious strategies.

About the Cost of Global Privacy in Density Estimation

We study non-parametric density estimation for densities in Lipschitz and Sobolev spaces, and under global privacy. In particular, we investigate regimes where the privacy budget is not supposed to be constant. We consider the classical definition of global differential privacy, but also the more recent notion of global concentrated differential privacy. We recover the result of Barber \& Duchi (2014) stating that histogram estimators are optimal against Lipschitz distributions for the L2 risk, and under regular differential privacy, and we extend it to other norms and notions of privacy. Then, we investigate higher degrees of smoothness, drawing two conclusions: First, and contrary to what happens with constant privacy budget (Wasserman \& Zhou, 2010), there are regimes where imposing privacy degrades the regular minimax risk of estimation on Sobolev densities. Second, so-called projection estimators are near-optimal against the same classes of densities in this new setup with pure differential privacy, but contrary to the constant privacy budget case, it comes at the cost of relaxation. With zero concentrated differential privacy, there is no need for relaxation, and we prove that the estimation is optimal.

Private Statistical Estimation of Many Quantiles

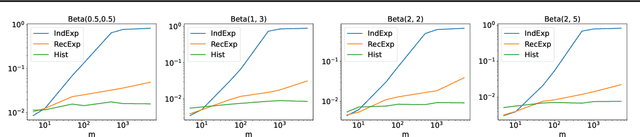
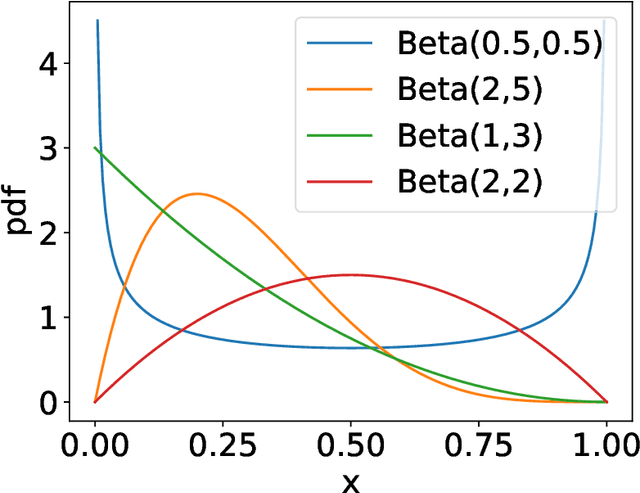
This work studies the estimation of many statistical quantiles under differential privacy. More precisely, given a distribution and access to i.i.d. samples from it, we study the estimation of the inverse of its cumulative distribution function (the quantile function) at specific points. For instance, this task is of key importance in private data generation. We present two different approaches. The first one consists in privately estimating the empirical quantiles of the samples and using this result as an estimator of the quantiles of the distribution. In particular, we study the statistical properties of the recently published algorithm introduced by Kaplan et al. 2022 that privately estimates the quantiles recursively. The second approach is to use techniques of density estimation in order to uniformly estimate the quantile function on an interval. In particular, we show that there is a tradeoff between the two methods. When we want to estimate many quantiles, it is better to estimate the density rather than estimating the quantile function at specific points.

Regret Analysis of the Stochastic Direct Search Method for Blind Resource Allocation

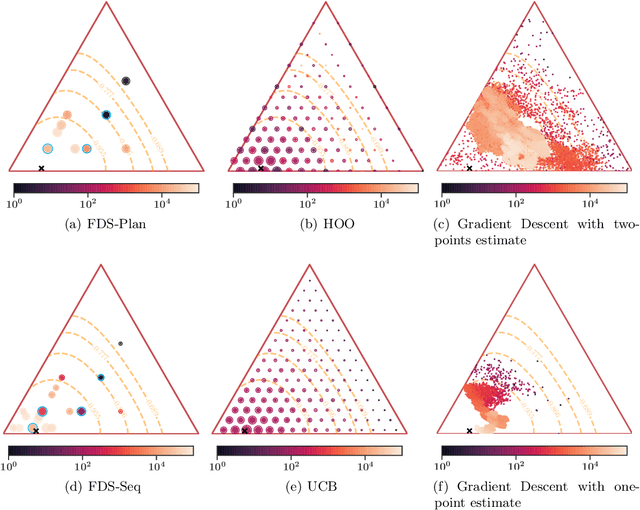
Motivated by programmatic advertising optimization, we consider the task of sequentially allocating budget across a set of resources. At every time step, a feasible allocation is chosen and only a corresponding random return is observed. The goal is to maximize the cumulative expected sum of returns. This is a realistic model for budget allocation across subdivisions of marketing campaigns, when the objective is to maximize the number of conversions. We study direct search (aka pattern search) methods for linearly constrained and derivative-free optimization in the presence of noise. Those algorithms are easy to implement and particularly suited to constrained optimization. They have not yet been analyzed from the perspective of cumulative regret. We provide a regret upper-bound of the order of T 2/3 in the general case. Our mathematical analysis also establishes, as a by-product, time-independent regret bounds in the deterministic, unconstrained case. We also propose an improved version of the method relying on sequential tests to accelerate the identification of descent directions.

On the Statistical Complexity of Estimation and Testing under Privacy Constraints

Producing statistics that respect the privacy of the samples while still maintaining their accuracy is an important topic of research. We study minimax lower bounds when the class of estimators is restricted to the differentially private ones. In particular, we show that characterizing the power of a distributional test under differential privacy can be done by solving a transport problem. With specific coupling constructions, this observation allows us to derivate Le Cam-type and Fano-type inequalities for both regular definitions of differential privacy and for divergence-based ones (based on Renyi divergence). We then proceed to illustrate our results on three simple, fully worked out examples. In particular, we show that the problem class has a huge importance on the provable degradation of utility due to privacy. For some problems, privacy leads to a provable degradation only when the rate of the privacy parameters is small enough whereas for other problem, the degradation systematically occurs under much looser hypotheses on the privacy parametters. Finally, we show that the known privacy guarantees of DP-SGLD, a private convex solver, when used to perform maximum likelihood, leads to an algorithm that is near-minimax optimal in both the sample size and the privacy tuning parameters of the problem for a broad class of parametric estimation procedures that includes exponential families.

On Best-Arm Identification with a Fixed Budget in Non-Parametric Multi-Armed Bandits

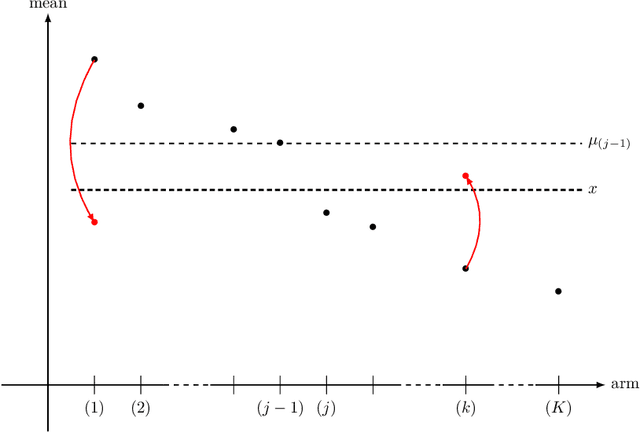
We lay the foundations of a non-parametric theory of best-arm identification in multi-armed bandits with a fixed budget T. We consider general, possibly non-parametric, models D for distributions over the arms; an overarching example is the model D = P(0,1) of all probability distributions over [0,1]. We propose upper bounds on the average log-probability of misidentifying the optimal arm based on information-theoretic quantities that correspond to infima over Kullback-Leibler divergences between some distributions in D and a given distribution. This is made possible by a refined analysis of the successive-rejects strategy of Audibert, Bubeck, and Munos (2010). We finally provide lower bounds on the same average log-probability, also in terms of the same new information-theoretic quantities; these lower bounds are larger when the (natural) assumptions on the considered strategies are stronger. All these new upper and lower bounds generalize existing bounds based, e.g., on gaps between distributions.

Private Quantiles Estimation in the Presence of Atoms

We address the differentially private estimation of multiple quantiles (MQ) of a dataset, a key building block in modern data analysis. We apply the recent non-smoothed Inverse Sensitivity (IS) mechanism to this specific problem and establish that the resulting method is closely related to the current state-of-the-art, the JointExp algorithm, sharing in particular the same computational complexity and a similar efficiency. However, we demonstrate both theoretically and empirically that (non-smoothed) JointExp suffers from an important lack of performance in the case of peaked distributions, with a potentially catastrophic impact in the presence of atoms. While its smoothed version would allow to leverage the performance guarantees of IS, it remains an open challenge to implement. As a proxy to fix the problem we propose a simple and numerically efficient method called Heuristically Smoothed JointExp (HSJointExp), which is endowed with performance guarantees for a broad class of distributions and achieves results that are orders of magnitude better on problematic datasets.

On the complexity of All $\varepsilon$-Best Arms Identification

We consider the problem introduced by \cite{Mason2020} of identifying all the $\varepsilon$-optimal arms in a finite stochastic multi-armed bandit with Gaussian rewards. In the fixed confidence setting, we give a lower bound on the number of samples required by any algorithm that returns the set of $\varepsilon$-good arms with a failure probability less than some risk level $\delta$. This bound writes as $T_{\varepsilon}^*(\mu)\log(1/\delta)$, where $T_{\varepsilon}^*(\mu)$ is a characteristic time that depends on the vector of mean rewards $\mu$ and the accuracy parameter $\varepsilon$. We also provide an efficient numerical method to solve the convex max-min program that defines the characteristic time. Our method is based on a complete characterization of the alternative bandit instances that the optimal sampling strategy needs to rule out, thus making our bound tighter than the one provided by \cite{Mason2020}. Using this method, we propose a Track-and-Stop algorithm that identifies the set of $\varepsilon$-good arms w.h.p and enjoys asymptotic optimality (when $\delta$ goes to zero) in terms of the expected sample complexity. Finally, using numerical simulations, we demonstrate our algorithm's advantage over state-of-the-art methods, even for moderate values of the risk parameter.

A/B/n Testing with Control in the Presence of Subpopulations

Motivated by A/B/n testing applications, we consider a finite set of distributions (called \emph{arms}), one of which is treated as a \emph{control}. We assume that the population is stratified into homogeneous subpopulations. At every time step, a subpopulation is sampled and an arm is chosen: the resulting observation is an independent draw from the arm conditioned on the subpopulation. The quality of each arm is assessed through a weighted combination of its subpopulation means. We propose a strategy for sequentially choosing one arm per time step so as to discover as fast as possible which arms, if any, have higher weighted expectation than the control. This strategy is shown to be asymptotically optimal in the following sense: if $\tau_\delta$ is the first time when the strategy ensures that it is able to output the correct answer with probability at least $1-\delta$, then $\mathbb{E}[\tau_\delta]$ grows linearly with $\log(1/\delta)$ at the exact optimal rate. This rate is identified in the paper in three different settings: (1) when the experimenter does not observe the subpopulation information, (2) when the subpopulation of each sample is observed but not chosen, and (3) when the experimenter can select the subpopulation from which each response is sampled. We illustrate the efficiency of the proposed strategy with numerical simulations on synthetic and real data collected from an A/B/n experiment.

Fast Rate Learning in Stochastic First Price Bidding

First-price auctions have largely replaced traditional bidding approaches based on Vickrey auctions in programmatic advertising. As far as learning is concerned, first-price auctions are more challenging because the optimal bidding strategy does not only depend on the value of the item but also requires some knowledge of the other bids. They have already given rise to several works in sequential learning, many of which consider models for which the value of the buyer or the opponents' maximal bid is chosen in an adversarial manner. Even in the simplest settings, this gives rise to algorithms whose regret grows as $\sqrt{T}$ with respect to the time horizon $T$. Focusing on the case where the buyer plays against a stationary stochastic environment, we show how to achieve significantly lower regret: when the opponents' maximal bid distribution is known we provide an algorithm whose regret can be as low as $\log^2(T)$; in the case where the distribution must be learnt sequentially, a generalization of this algorithm can achieve $T^{1/3+ \epsilon}$ regret, for any $\epsilon>0$. To obtain these results, we introduce two novel ideas that can be of interest in their own right. First, by transposing results obtained in the posted price setting, we provide conditions under which the first-price biding utility is locally quadratic around its optimum. Second, we leverage the observation that, on small sub-intervals, the concentration of the variations of the empirical distribution function may be controlled more accurately than by using the classical Dvoretzky-Kiefer-Wolfowitz inequality. Numerical simulations confirm that our algorithms converge much faster than alternatives proposed in the literature for various bid distributions, including for bids collected on an actual programmatic advertising platform.