Clément Gastaud
CB
Private Quantiles Estimation in the Presence of Atoms
Feb 15, 2022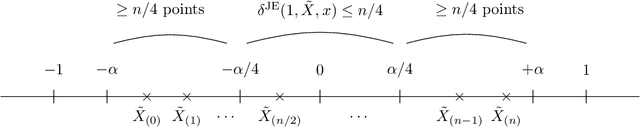


Abstract:We address the differentially private estimation of multiple quantiles (MQ) of a dataset, a key building block in modern data analysis. We apply the recent non-smoothed Inverse Sensitivity (IS) mechanism to this specific problem and establish that the resulting method is closely related to the current state-of-the-art, the JointExp algorithm, sharing in particular the same computational complexity and a similar efficiency. However, we demonstrate both theoretically and empirically that (non-smoothed) JointExp suffers from an important lack of performance in the case of peaked distributions, with a potentially catastrophic impact in the presence of atoms. While its smoothed version would allow to leverage the performance guarantees of IS, it remains an open challenge to implement. As a proxy to fix the problem we propose a simple and numerically efficient method called Heuristically Smoothed JointExp (HSJointExp), which is endowed with performance guarantees for a broad class of distributions and achieves results that are orders of magnitude better on problematic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge