About the Cost of Global Privacy in Density Estimation

We study non-parametric density estimation for densities in Lipschitz and Sobolev spaces, and under global privacy. In particular, we investigate regimes where the privacy budget is not supposed to be constant. We consider the classical definition of global differential privacy, but also the more recent notion of global concentrated differential privacy. We recover the result of Barber \& Duchi (2014) stating that histogram estimators are optimal against Lipschitz distributions for the L2 risk, and under regular differential privacy, and we extend it to other norms and notions of privacy. Then, we investigate higher degrees of smoothness, drawing two conclusions: First, and contrary to what happens with constant privacy budget (Wasserman \& Zhou, 2010), there are regimes where imposing privacy degrades the regular minimax risk of estimation on Sobolev densities. Second, so-called projection estimators are near-optimal against the same classes of densities in this new setup with pure differential privacy, but contrary to the constant privacy budget case, it comes at the cost of relaxation. With zero concentrated differential privacy, there is no need for relaxation, and we prove that the estimation is optimal.

Sparsity in neural networks can improve their privacy

This article measures how sparsity can make neural networks more robust to membership inference attacks. The obtained empirical results show that sparsity improves the privacy of the network, while preserving comparable performances on the task at hand. This empirical study completes and extends existing literature.

Sparsity in neural networks can increase their privacy

This article measures how sparsity can make neural networks more robust to membership inference attacks. The obtained empirical results show that sparsity improves the privacy of the network, while preserving comparable performances on the task at hand. This empirical study completes and extends existing literature.

Private Statistical Estimation of Many Quantiles

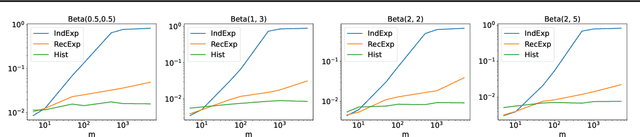
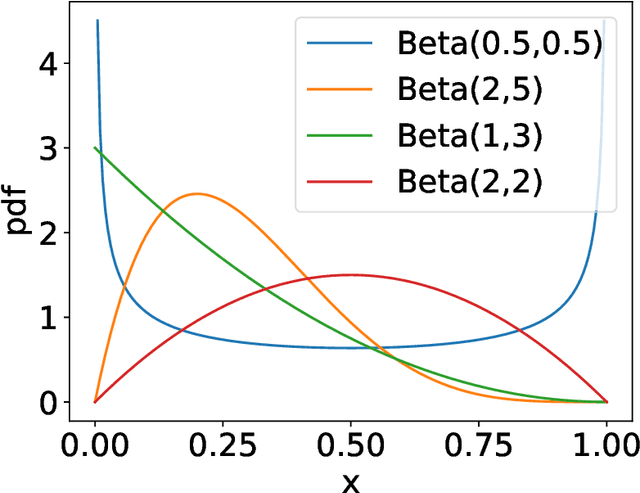
This work studies the estimation of many statistical quantiles under differential privacy. More precisely, given a distribution and access to i.i.d. samples from it, we study the estimation of the inverse of its cumulative distribution function (the quantile function) at specific points. For instance, this task is of key importance in private data generation. We present two different approaches. The first one consists in privately estimating the empirical quantiles of the samples and using this result as an estimator of the quantiles of the distribution. In particular, we study the statistical properties of the recently published algorithm introduced by Kaplan et al. 2022 that privately estimates the quantiles recursively. The second approach is to use techniques of density estimation in order to uniformly estimate the quantile function on an interval. In particular, we show that there is a tradeoff between the two methods. When we want to estimate many quantiles, it is better to estimate the density rather than estimating the quantile function at specific points.

On the Statistical Complexity of Estimation and Testing under Privacy Constraints

Producing statistics that respect the privacy of the samples while still maintaining their accuracy is an important topic of research. We study minimax lower bounds when the class of estimators is restricted to the differentially private ones. In particular, we show that characterizing the power of a distributional test under differential privacy can be done by solving a transport problem. With specific coupling constructions, this observation allows us to derivate Le Cam-type and Fano-type inequalities for both regular definitions of differential privacy and for divergence-based ones (based on Renyi divergence). We then proceed to illustrate our results on three simple, fully worked out examples. In particular, we show that the problem class has a huge importance on the provable degradation of utility due to privacy. For some problems, privacy leads to a provable degradation only when the rate of the privacy parameters is small enough whereas for other problem, the degradation systematically occurs under much looser hypotheses on the privacy parametters. Finally, we show that the known privacy guarantees of DP-SGLD, a private convex solver, when used to perform maximum likelihood, leads to an algorithm that is near-minimax optimal in both the sample size and the privacy tuning parameters of the problem for a broad class of parametric estimation procedures that includes exponential families.

Private Quantiles Estimation in the Presence of Atoms

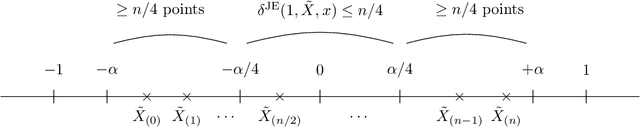
We address the differentially private estimation of multiple quantiles (MQ) of a dataset, a key building block in modern data analysis. We apply the recent non-smoothed Inverse Sensitivity (IS) mechanism to this specific problem and establish that the resulting method is closely related to the current state-of-the-art, the JointExp algorithm, sharing in particular the same computational complexity and a similar efficiency. However, we demonstrate both theoretically and empirically that (non-smoothed) JointExp suffers from an important lack of performance in the case of peaked distributions, with a potentially catastrophic impact in the presence of atoms. While its smoothed version would allow to leverage the performance guarantees of IS, it remains an open challenge to implement. As a proxy to fix the problem we propose a simple and numerically efficient method called Heuristically Smoothed JointExp (HSJointExp), which is endowed with performance guarantees for a broad class of distributions and achieves results that are orders of magnitude better on problematic datasets.

Extraction of Nystagmus Patterns from Eye-Tracker Data with Convolutional Sparse Coding

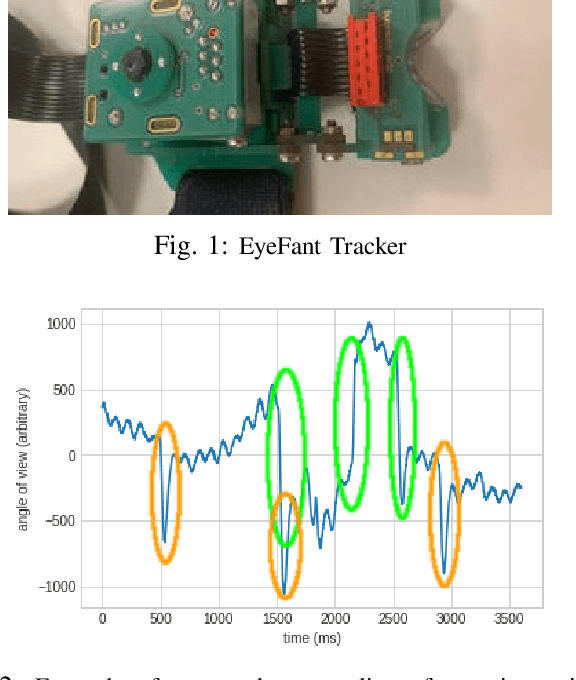
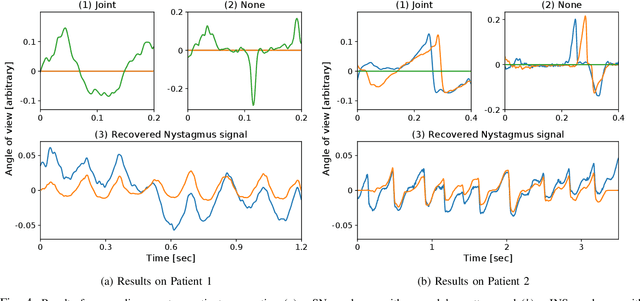
The analysis of the Nystagmus waveforms from eye-tracking records is crucial for the clinicial interpretation of this pathological movement. A major issue to automatize this analysis is the presence of natural eye movements and eye blink artefacts that are mixed with the signal of interest. We propose a method based on Convolutional Dictionary Learning that is able to automaticcaly highlight the Nystagmus waveforms, separating the natural motion from the pathological movements. We show on simulated signals that our method can indeed improve the pattern recovery rate and provide clinical examples to illustrate how this algorithm performs.