Claire Vernade
L2S
Non-Stationary Lipschitz Bandits
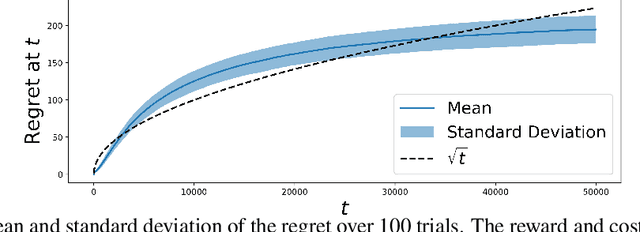
May 24, 2025Abstract:We study the problem of non-stationary Lipschitz bandits, where the number of actions is infinite and the reward function, satisfying a Lipschitz assumption, can change arbitrarily over time. We design an algorithm that adaptively tracks the recently introduced notion of significant shifts, defined by large deviations of the cumulative reward function. To detect such reward changes, our algorithm leverages a hierarchical discretization of the action space. Without requiring any prior knowledge of the non-stationarity, our algorithm achieves a minimax-optimal dynamic regret bound of $\mathcal{\widetilde{O}}(\tilde{L}^{1/3}T^{2/3})$, where $\tilde{L}$ is the number of significant shifts and $T$ the horizon. This result provides the first optimal guarantee in this setting.
Put CASH on Bandits: A Max K-Armed Problem for Automated Machine Learning
May 08, 2025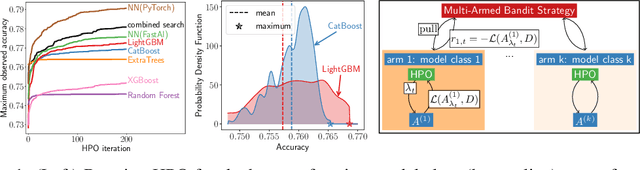
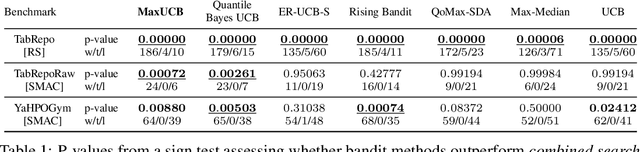
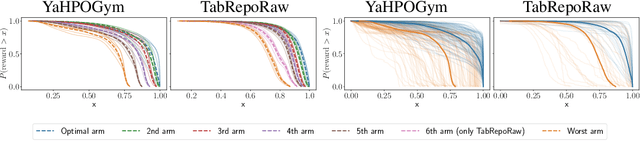
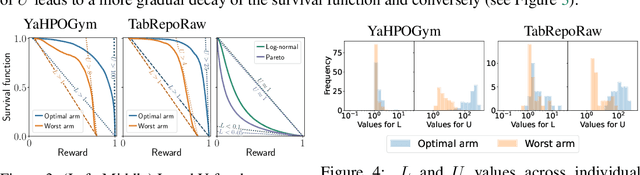
Abstract:The Combined Algorithm Selection and Hyperparameter optimization (CASH) is a challenging resource allocation problem in the field of AutoML. We propose MaxUCB, a max $k$-armed bandit method to trade off exploring different model classes and conducting hyperparameter optimization. MaxUCB is specifically designed for the light-tailed and bounded reward distributions arising in this setting and, thus, provides an efficient alternative compared to classic max $k$-armed bandit methods assuming heavy-tailed reward distributions. We theoretically and empirically evaluate our method on four standard AutoML benchmarks, demonstrating superior performance over prior approaches.
Quantization-Free Autoregressive Action Transformer
Mar 18, 2025
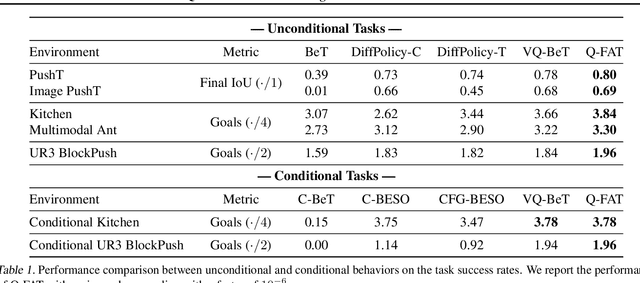
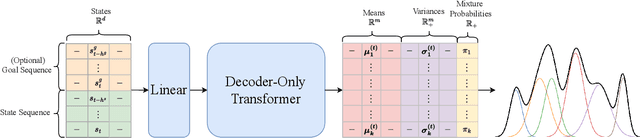
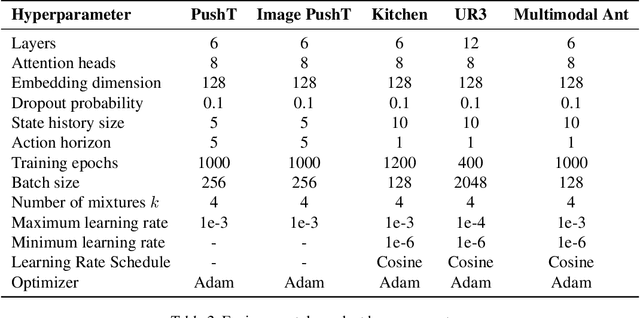
Abstract:Current transformer-based imitation learning approaches introduce discrete action representations and train an autoregressive transformer decoder on the resulting latent code. However, the initial quantization breaks the continuous structure of the action space thereby limiting the capabilities of the generative model. We propose a quantization-free method instead that leverages Generative Infinite-Vocabulary Transformers (GIVT) as a direct, continuous policy parametrization for autoregressive transformers. This simplifies the imitation learning pipeline while achieving state-of-the-art performance on a variety of popular simulated robotics tasks. We enhance our policy roll-outs by carefully studying sampling algorithms, further improving the results.
Clustered KL-barycenter design for policy evaluation
Mar 04, 2025Abstract:In the context of stochastic bandit models, this article examines how to design sample-efficient behavior policies for the importance sampling evaluation of multiple target policies. From importance sampling theory, it is well established that sample efficiency is highly sensitive to the KL divergence between the target and importance sampling distributions. We first analyze a single behavior policy defined as the KL-barycenter of the target policies. Then, we refine this approach by clustering the target policies into groups with small KL divergences and assigning each cluster its own KL-barycenter as a behavior policy. This clustered KL-based policy evaluation (CKL-PE) algorithm provides a novel perspective on optimal policy selection. We prove upper bounds on the sample complexity of our method and demonstrate its effectiveness with numerical validation.
Efficient Risk-sensitive Planning via Entropic Risk Measures
Feb 27, 2025Abstract:Risk-sensitive planning aims to identify policies maximizing some tail-focused metrics in Markov Decision Processes (MDPs). Such an optimization task can be very costly for the most widely used and interpretable metrics such as threshold probabilities or (Conditional) Values at Risk. Indeed, previous work showed that only Entropic Risk Measures (EntRM) can be efficiently optimized through dynamic programming, leaving a hard-to-interpret parameter to choose. We show that the computation of the full set of optimal policies for EntRM across parameter values leads to tight approximations for the metrics of interest. We prove that this optimality front can be computed effectively thanks to a novel structural analysis and smoothness properties of entropic risks. Empirical results demonstrate that our approach achieves strong performance in a variety of decision-making scenarios.
Variational Bayes Portfolio Construction
Nov 09, 2024Abstract:Portfolio construction is the science of balancing reward and risk; it is at the core of modern finance. In this paper, we tackle the question of optimal decision-making within a Bayesian paradigm, starting from a decision-theoretic formulation. Despite the inherent intractability of the optimal decision in any interesting scenarios, we manage to rewrite it as a saddle-point problem. Leveraging the literature on variational Bayes (VB), we propose a relaxation of the original problem. This novel methodology results in an efficient algorithm that not only performs well but is also provably convergent. Furthermore, we provide theoretical results on the statistical consistency of the resulting decision with the optimal Bayesian decision. Using real data, our proposal significantly enhances the speed and scalability of portfolio selection problems. We benchmark our results against state-of-the-art algorithms, as well as a Monte Carlo algorithm targeting the optimal decision.
Online Decision Deferral under Budget Constraints
Sep 30, 2024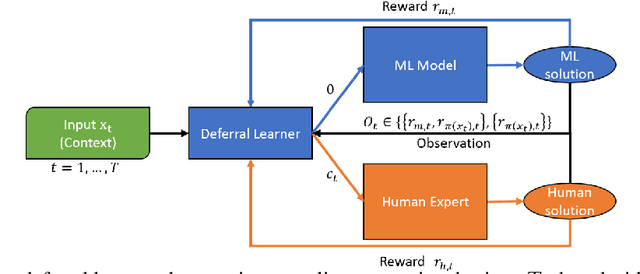
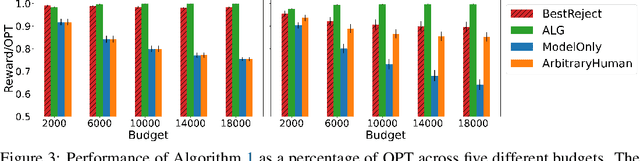
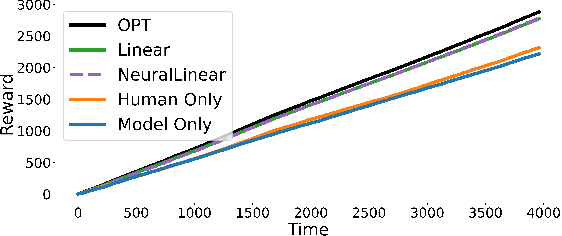
Abstract:Machine Learning (ML) models are increasingly used to support or substitute decision making. In applications where skilled experts are a limited resource, it is crucial to reduce their burden and automate decisions when the performance of an ML model is at least of equal quality. However, models are often pre-trained and fixed, while tasks arrive sequentially and their distribution may shift. In that case, the respective performance of the decision makers may change, and the deferral algorithm must remain adaptive. We propose a contextual bandit model of this online decision making problem. Our framework includes budget constraints and different types of partial feedback models. Beyond the theoretical guarantees of our algorithm, we propose efficient extensions that achieve remarkable performance on real-world datasets.
A Pontryagin Perspective on Reinforcement Learning
May 28, 2024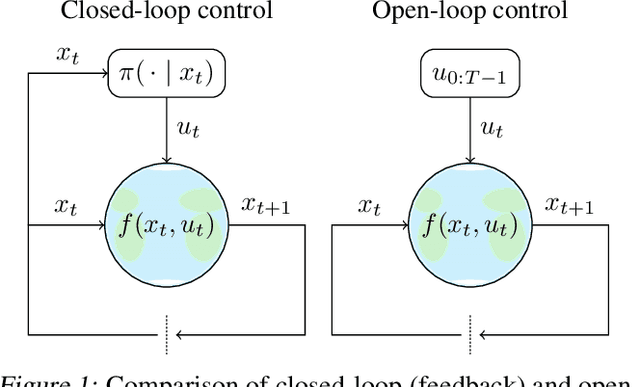


Abstract:Reinforcement learning has traditionally focused on learning state-dependent policies to solve optimal control problems in a closed-loop fashion. In this work, we introduce the paradigm of open-loop reinforcement learning where a fixed action sequence is learned instead. We present three new algorithms: one robust model-based method and two sample-efficient model-free methods. Rather than basing our algorithms on Bellman's equation from dynamic programming, our work builds on Pontryagin's principle from the theory of open-loop optimal control. We provide convergence guarantees and evaluate all methods empirically on a pendulum swing-up task, as well as on two high-dimensional MuJoCo tasks, demonstrating remarkable performance compared to existing baselines.
Prior-Dependent Allocations for Bayesian Fixed-Budget Best-Arm Identification in Structured Bandits
Feb 08, 2024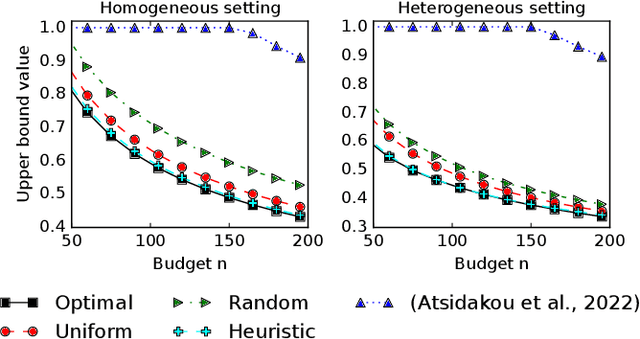
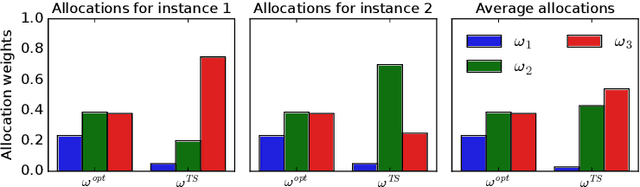
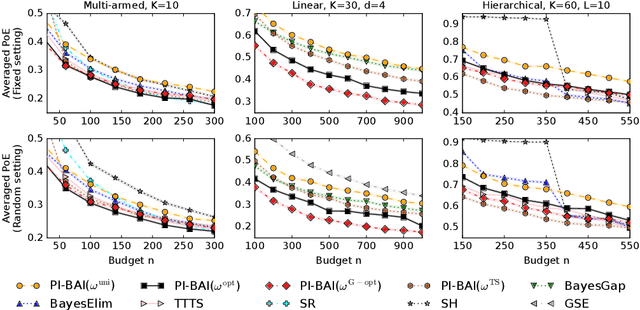
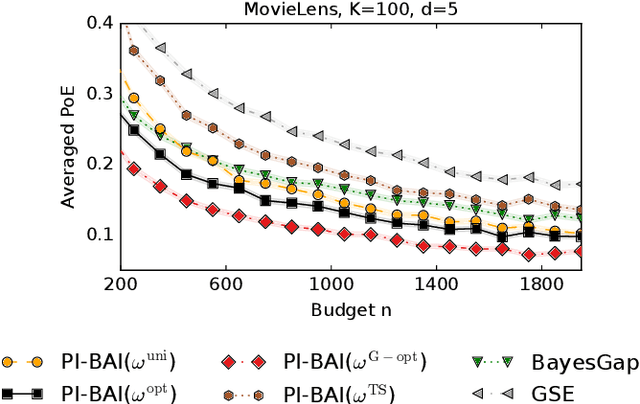
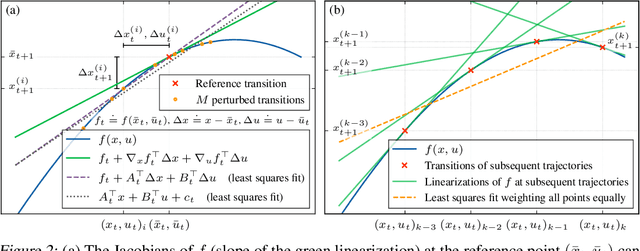
Abstract:We study the problem of Bayesian fixed-budget best-arm identification (BAI) in structured bandits. We propose an algorithm that uses fixed allocations based on the prior information and the structure of the environment. We provide theoretical bounds on its performance across diverse models, including the first prior-dependent upper bounds for linear and hierarchical BAI. Our key contribution is introducing new proof methods that result in tighter bounds for multi-armed BAI compared to existing methods. We extensively compare our approach to other fixed-budget BAI methods, demonstrating its consistent and robust performance in various settings. Our work improves our understanding of Bayesian fixed-budget BAI in structured bandits and highlights the effectiveness of our approach in practical scenarios.
Beyond Average Return in Markov Decision Processes
Oct 31, 2023Abstract:What are the functionals of the reward that can be computed and optimized exactly in Markov Decision Processes? In the finite-horizon, undiscounted setting, Dynamic Programming (DP) can only handle these operations efficiently for certain classes of statistics. We summarize the characterization of these classes for policy evaluation, and give a new answer for the planning problem. Interestingly, we prove that only generalized means can be optimized exactly, even in the more general framework of Distributional Reinforcement Learning (DistRL).DistRL permits, however, to evaluate other functionals approximately. We provide error bounds on the resulting estimators, and discuss the potential of this approach as well as its limitations.These results contribute to advancing the theory of Markov Decision Processes by examining overall characteristics of the return, and particularly risk-conscious strategies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge