Is One Layer Enough? Understanding Inference Dynamics in Tabular Foundation Models

Transformer-based tabular foundation models (TFMs) dominate small to medium tabular predictive benchmark tasks, yet their inference mechanisms remain largely unexplored. We present the first large-scale mechanistic study of layerwise dynamics in 6 state-of-the-art tabular in-context learning models. We explore how predictions emerge across depth, identify distinct stages of inference and reveal latent-space dynamics that differ from those of language models. Our findings indicate substantial depthwise redundancy across multiple models, suggesting iterative refinement with overlapping computations during inference stages. Guided by these insights, we design a proof-of-concept, looped single-layer model that uses only 20% of the original model's parameters while achieving comparable performance. The code is available at https://github.com/amirbalef/is_one_layer_enough.

Towards Understanding Layer Contributions in Tabular In-Context Learning Models

Despite the architectural similarities between tabular in-context learning (ICL) models and large language models (LLMs), little is known about how individual layers contribute to tabular prediction. In this paper, we investigate how the latent spaces evolve across layers in tabular ICL models, identify potential redundant layers, and compare these dynamics with those observed in LLMs. We analyze TabPFN and TabICL through the "layers as painters" perspective, finding that only subsets of layers share a common representational language, suggesting structural redundancy and offering opportunities for model compression and improved interpretability.

Put CASH on Bandits: A Max K-Armed Problem for Automated Machine Learning

The Combined Algorithm Selection and Hyperparameter optimization (CASH) is a challenging resource allocation problem in the field of AutoML. We propose MaxUCB, a max $k$-armed bandit method to trade off exploring different model classes and conducting hyperparameter optimization. MaxUCB is specifically designed for the light-tailed and bounded reward distributions arising in this setting and, thus, provides an efficient alternative compared to classic max $k$-armed bandit methods assuming heavy-tailed reward distributions. We theoretically and empirically evaluate our method on four standard AutoML benchmarks, demonstrating superior performance over prior approaches.

Piecewise-Stationary Combinatorial Semi-Bandit with Causally Related Rewards

We study the piecewise stationary combinatorial semi-bandit problem with causally related rewards. In our nonstationary environment, variations in the base arms' distributions, causal relationships between rewards, or both, change the reward generation process. In such an environment, an optimal decision-maker must follow both sources of change and adapt accordingly. The problem becomes aggravated in the combinatorial semi-bandit setting, where the decision-maker only observes the outcome of the selected bundle of arms. The core of our proposed policy is the Upper Confidence Bound (UCB) algorithm. We assume the agent relies on an adaptive approach to overcome the challenge. More specifically, it employs a change-point detector based on the Generalized Likelihood Ratio (GLR) test. Besides, we introduce the notion of group restart as a new alternative restarting strategy in the decision making process in structured environments. Finally, our algorithm integrates a mechanism to trace the variations of the underlying graph structure, which captures the causal relationships between the rewards in the bandit setting. Theoretically, we establish a regret upper bound that reflects the effects of the number of structural- and distribution changes on the performance. The outcome of our numerical experiments in real-world scenarios exhibits applicability and superior performance of our proposal compared to the state-of-the-art benchmarks.

Piecewise-Stationary Multi-Objective Multi-Armed Bandit with Application to Joint Communications and Sensing

We study a multi-objective multi-armed bandit problem in a dynamic environment. The problem portrays a decision-maker that sequentially selects an arm from a given set. If selected, each action produces a reward vector, where every element follows a piecewise-stationary Bernoulli distribution. The agent aims at choosing an arm among the Pareto optimal set of arms to minimize its regret. We propose a Pareto generic upper confidence bound (UCB)-based algorithm with change detection to solve this problem. By developing the essential inequalities for multi-dimensional spaces, we establish that our proposal guarantees a regret bound in the order of $\gamma_T\log(T/{\gamma_T})$ when the number of breakpoints $\gamma_T$ is known. Without this assumption, the regret bound of our algorithm is $\gamma_T\log(T)$. Finally, we formulate an energy-efficient waveform design problem in an integrated communication and sensing system as a toy example. Numerical experiments on the toy example and synthetic and real-world datasets demonstrate the efficiency of our policy compared to the current methods.

DONE: Distributed Approximate Newton-type Method for Federated Edge Learning

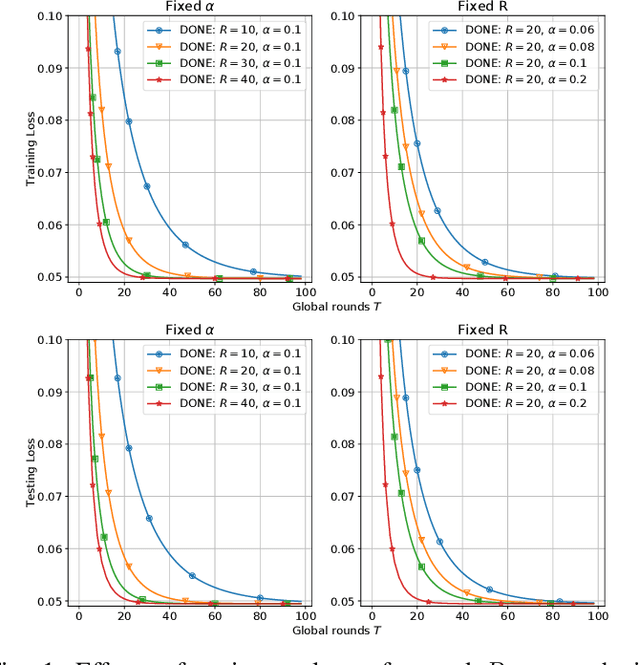
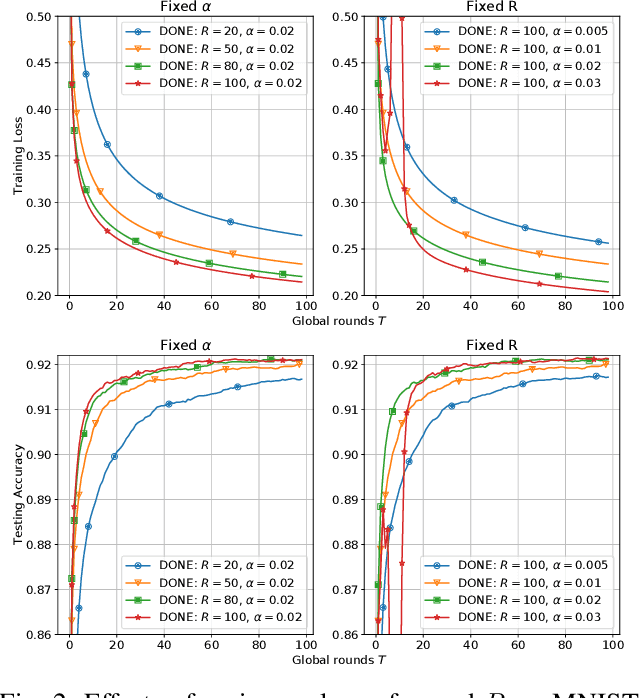
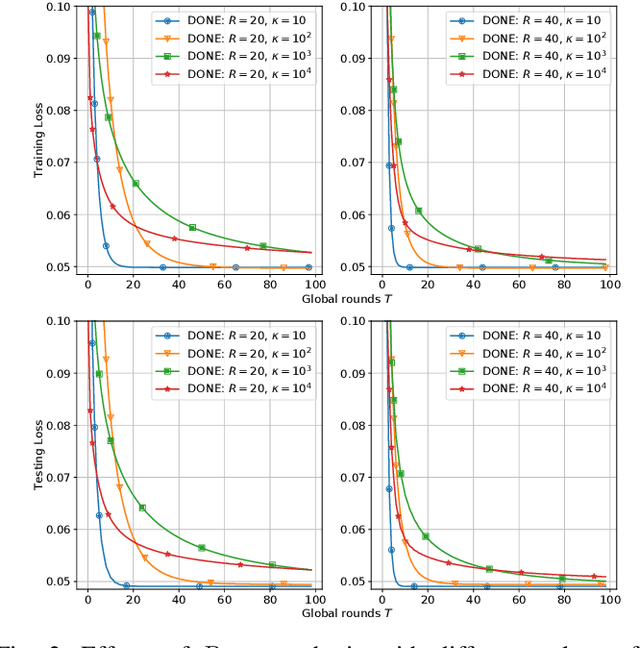
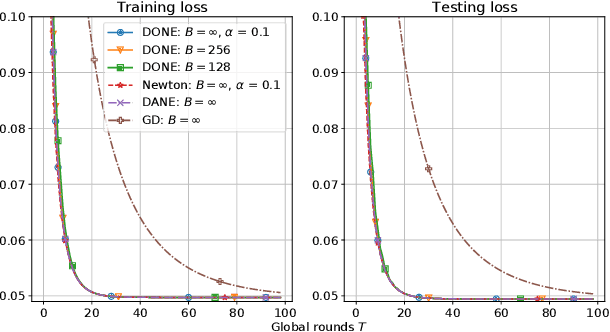
There is growing interest in applying distributed machine learning to edge computing, forming federated edge learning. Federated edge learning faces non-i.i.d and heterogeneous data, and the communication between edge workers, possibly through distant locations and with unstable wireless networks, is more costly than their local computational overhead. Here, we propose DONE, a distributed approximate Newton-type algorithm with fast convergence rate for communication-efficient federated edge learning. First, with strongly convex and smooth loss functions, DONE can approximately produce the Newton direction in a distributed manner by using the classical Richardson iteration on each edge worker. Second, we prove that DONE has linear-quadratic convergence and analyze its computation and communication complexities. Finally, the experimental results with non-i.i.d. and heterogeneous data show that DONE attains comparable performance to the Newton's method. Notably, DONE requires fewer communication iterations compared to distributed gradient descent and outperforms DANE, a similar and state-of-the-art approach, in the case of non-quadratic loss functions.