DONE: Distributed Approximate Newton-type Method for Federated Edge Learning
Paper and Code
Jan 17, 2021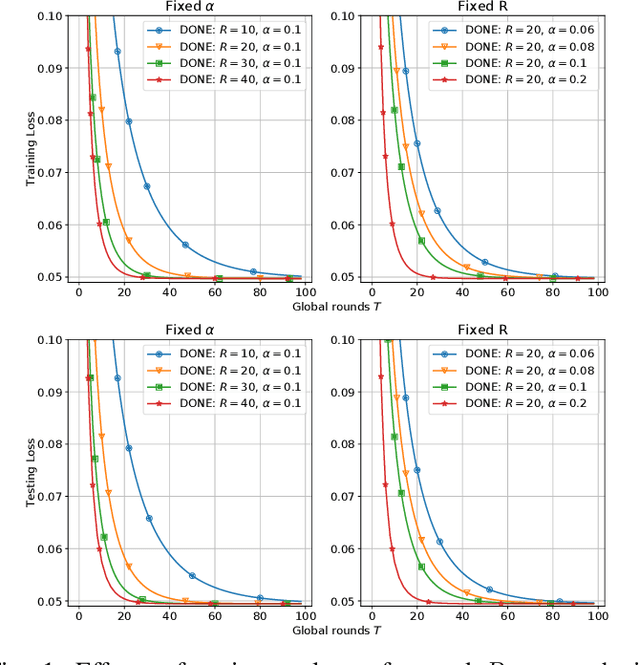
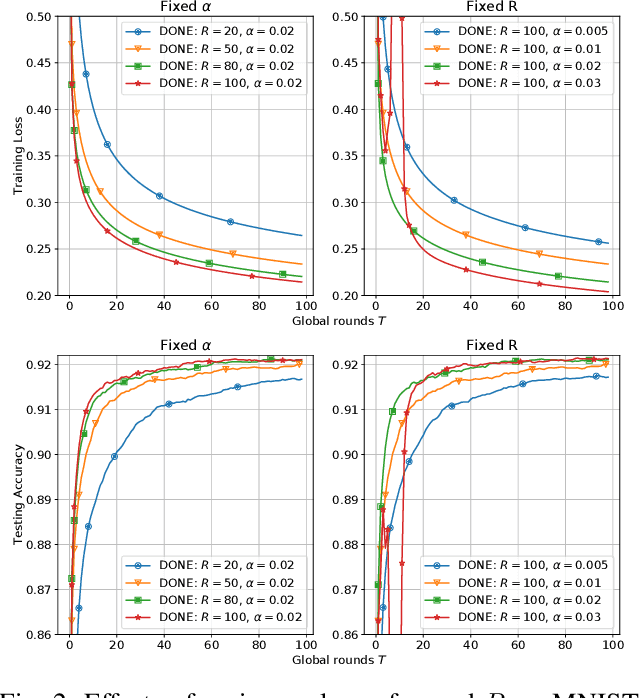
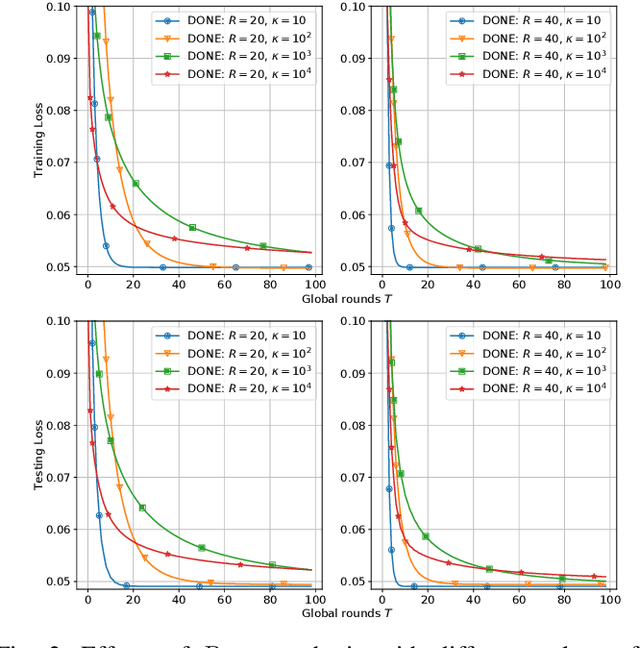
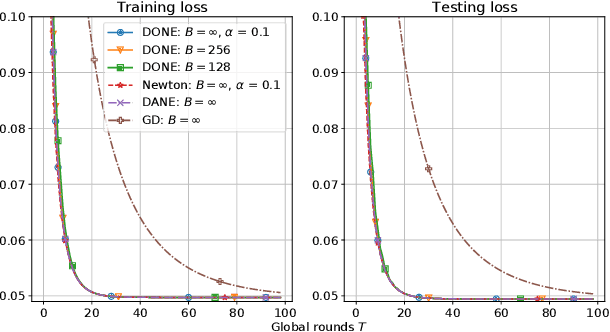
There is growing interest in applying distributed machine learning to edge computing, forming federated edge learning. Federated edge learning faces non-i.i.d and heterogeneous data, and the communication between edge workers, possibly through distant locations and with unstable wireless networks, is more costly than their local computational overhead. Here, we propose DONE, a distributed approximate Newton-type algorithm with fast convergence rate for communication-efficient federated edge learning. First, with strongly convex and smooth loss functions, DONE can approximately produce the Newton direction in a distributed manner by using the classical Richardson iteration on each edge worker. Second, we prove that DONE has linear-quadratic convergence and analyze its computation and communication complexities. Finally, the experimental results with non-i.i.d. and heterogeneous data show that DONE attains comparable performance to the Newton's method. Notably, DONE requires fewer communication iterations compared to distributed gradient descent and outperforms DANE, a similar and state-of-the-art approach, in the case of non-quadratic loss functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge