On the Generalization of Wasserstein Robust Federated Learning

In federated learning, participating clients typically possess non-i.i.d. data, posing a significant challenge to generalization to unseen distributions. To address this, we propose a Wasserstein distributionally robust optimization scheme called WAFL. Leveraging its duality, we frame WAFL as an empirical surrogate risk minimization problem, and solve it using a local SGD-based algorithm with convergence guarantees. We show that the robustness of WAFL is more general than related approaches, and the generalization bound is robust to all adversarial distributions inside the Wasserstein ball (ambiguity set). Since the center location and radius of the Wasserstein ball can be suitably modified, WAFL shows its applicability not only in robustness but also in domain adaptation. Through empirical evaluation, we demonstrate that WAFL generalizes better than the vanilla FedAvg in non-i.i.d. settings, and is more robust than other related methods in distribution shift settings. Further, using benchmark datasets we show that WAFL is capable of generalizing to unseen target domains.

Channel Estimation in RIS-assisted Downlink Massive MIMO: A Learning-Based Approach

For downlink massive multiple-input multiple-output (MIMO) operating in time-division duplex protocol, users can decode the signals effectively by only utilizing the channel statistics as long as channel hardening holds. However, in a reconfigurable intelligent surface (RIS)-assisted massive MIMO system, the propagation channels may be less hardened due to the extra random fluctuations of the effective channel gains. To address this issue, we propose a learning-based method that trains a neural network to learn a mapping between the received downlink signal and the effective channel gains. The proposed method does not require any downlink pilots and statistical information of interfering users. Numerical results show that, in terms of mean-square error of the channel estimation, our proposed learning-based method outperforms the state-of-the-art methods, especially when the light-of-sight (LoS) paths are dominated by non-LoS paths with a low level of channel hardening, e.g., in the cases of small numbers of RIS elements and/or base station antennas.

FedU: A Unified Framework for Federated Multi-Task Learning with Laplacian Regularization

Federated multi-task learning (FMTL) has emerged as a natural choice to capture the statistical diversity among the clients in federated learning. To unleash the potential of FMTL beyond statistical diversity, we formulate a new FMTL problem FedU using Laplacian regularization, which can explicitly leverage relationships among the clients for multi-task learning. We first show that FedU provides a unified framework covering a wide range of problems such as conventional federated learning, personalized federated learning, few-shot learning, and stratified model learning. We then propose algorithms including both communication-centralized and decentralized schemes to learn optimal models of FedU. Theoretically, we show that the convergence rates of both FedU's algorithms achieve linear speedup for strongly convex and sublinear speedup of order $1/2$ for nonconvex objectives. While the analysis of FedU is applicable to both strongly convex and nonconvex loss functions, the conventional FMTL algorithm MOCHA, which is based on CoCoA framework, is only applicable to convex case. Experimentally, we verify that FedU outperforms the vanilla FedAvg, MOCHA, as well as pFedMe and Per-FedAvg in personalized federated learning.

DONE: Distributed Approximate Newton-type Method for Federated Edge Learning

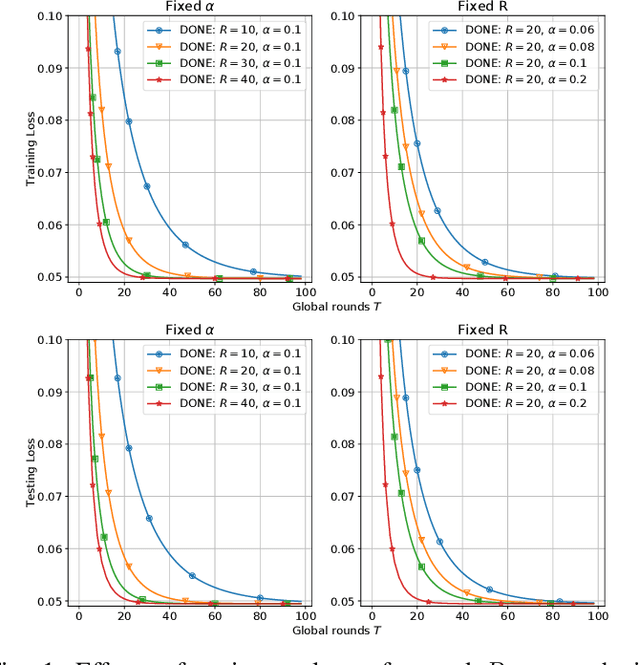
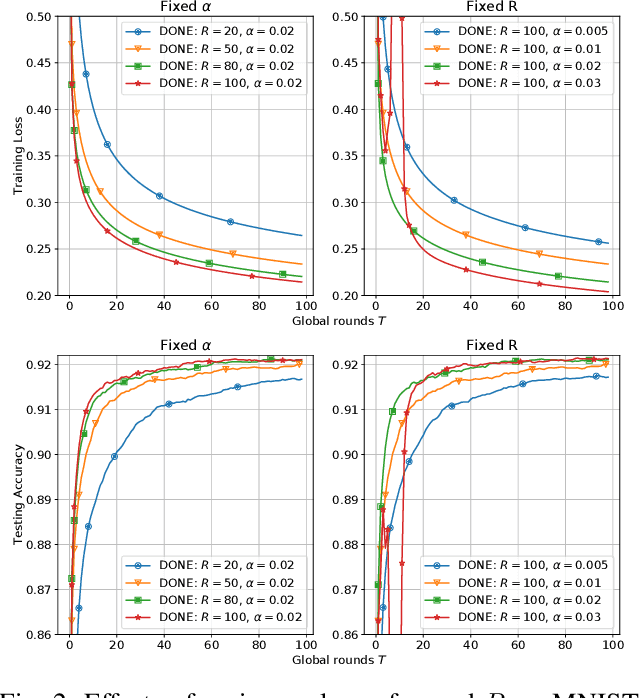
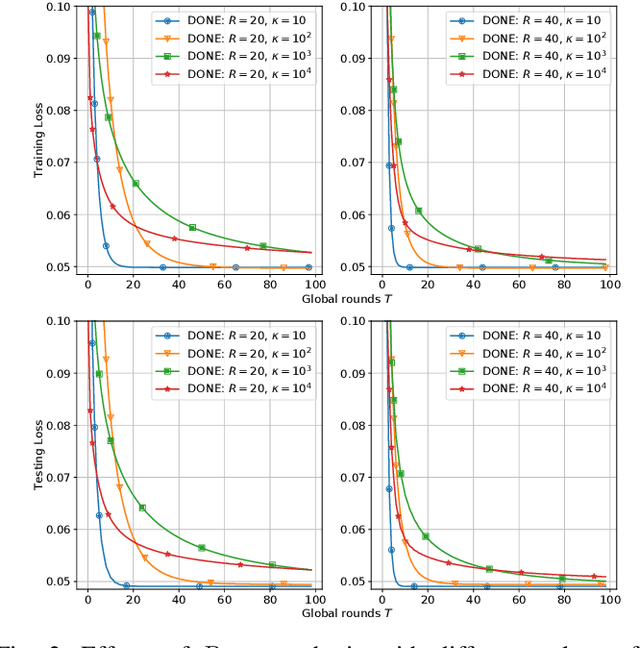
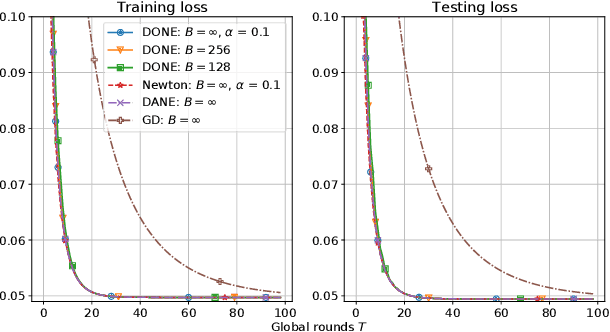
There is growing interest in applying distributed machine learning to edge computing, forming federated edge learning. Federated edge learning faces non-i.i.d and heterogeneous data, and the communication between edge workers, possibly through distant locations and with unstable wireless networks, is more costly than their local computational overhead. Here, we propose DONE, a distributed approximate Newton-type algorithm with fast convergence rate for communication-efficient federated edge learning. First, with strongly convex and smooth loss functions, DONE can approximately produce the Newton direction in a distributed manner by using the classical Richardson iteration on each edge worker. Second, we prove that DONE has linear-quadratic convergence and analyze its computation and communication complexities. Finally, the experimental results with non-i.i.d. and heterogeneous data show that DONE attains comparable performance to the Newton's method. Notably, DONE requires fewer communication iterations compared to distributed gradient descent and outperforms DANE, a similar and state-of-the-art approach, in the case of non-quadratic loss functions.

Personalized Federated Learning with Moreau Envelopes

Federated learning (FL) is a decentralized and privacy-preserving machine learning technique in which a group of clients collaborate with a server to learn a global model without sharing clients' data. One challenge associated with FL is statistical diversity among clients, which restricts the global model from delivering good performance on each client's task. To address this, we propose an algorithm for personalized FL (pFedMe) using Moreau envelopes as clients' regularized loss functions, which help decouple personalized model optimization from the global model learning in a bi-level problem stylized for personalized FL. Theoretically, we show that pFedMe's convergence rate is state-of-the-art: achieving quadratic speedup for strongly convex and sublinear speedup of order 2/3 for smooth nonconvex objectives. Experimentally, we verify that pFedMe excels at empirical performance compared with the vanilla FedAvg and Per-FedAvg, a meta-learning based personalized FL algorithm.