Piecewise-Stationary Combinatorial Semi-Bandit with Causally Related Rewards

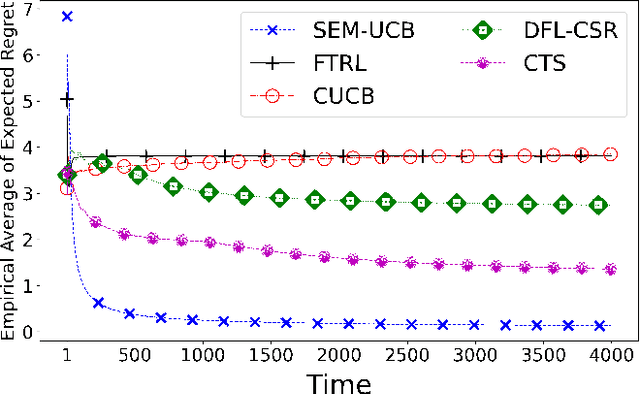
We study the piecewise stationary combinatorial semi-bandit problem with causally related rewards. In our nonstationary environment, variations in the base arms' distributions, causal relationships between rewards, or both, change the reward generation process. In such an environment, an optimal decision-maker must follow both sources of change and adapt accordingly. The problem becomes aggravated in the combinatorial semi-bandit setting, where the decision-maker only observes the outcome of the selected bundle of arms. The core of our proposed policy is the Upper Confidence Bound (UCB) algorithm. We assume the agent relies on an adaptive approach to overcome the challenge. More specifically, it employs a change-point detector based on the Generalized Likelihood Ratio (GLR) test. Besides, we introduce the notion of group restart as a new alternative restarting strategy in the decision making process in structured environments. Finally, our algorithm integrates a mechanism to trace the variations of the underlying graph structure, which captures the causal relationships between the rewards in the bandit setting. Theoretically, we establish a regret upper bound that reflects the effects of the number of structural- and distribution changes on the performance. The outcome of our numerical experiments in real-world scenarios exhibits applicability and superior performance of our proposal compared to the state-of-the-art benchmarks.

Linear Combinatorial Semi-Bandit with Causally Related Rewards

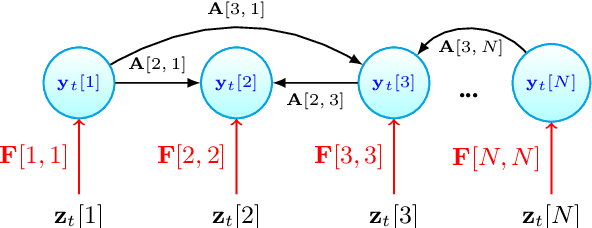
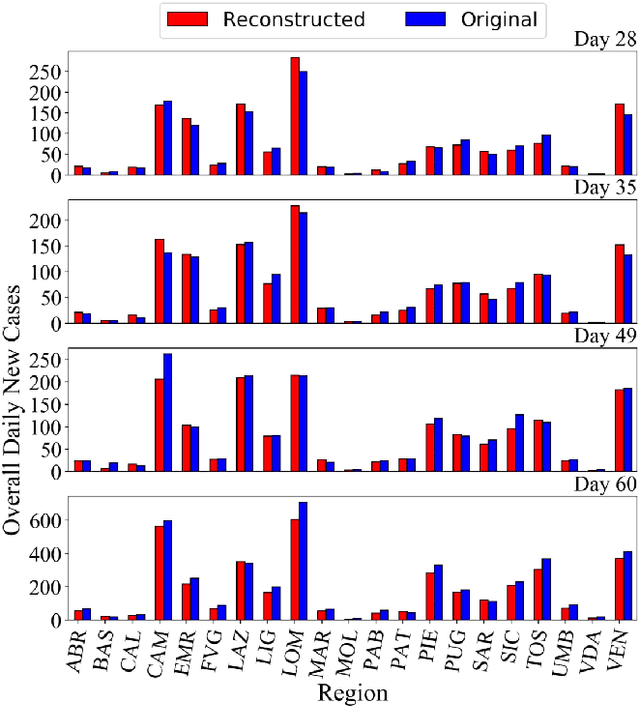
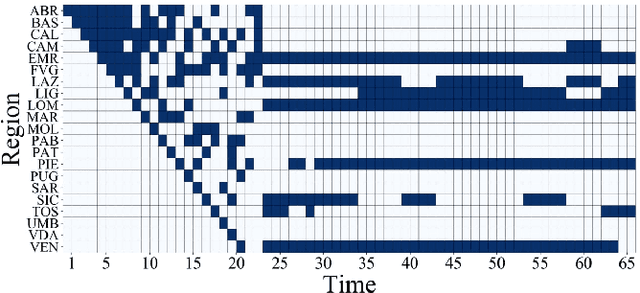
In a sequential decision-making problem, having a structural dependency amongst the reward distributions associated with the arms makes it challenging to identify a subset of alternatives that guarantees the optimal collective outcome. Thus, besides individual actions' reward, learning the causal relations is essential to improve the decision-making strategy. To solve the two-fold learning problem described above, we develop the 'combinatorial semi-bandit framework with causally related rewards', where we model the causal relations by a directed graph in a stationary structural equation model. The nodal observation in the graph signal comprises the corresponding base arm's instantaneous reward and an additional term resulting from the causal influences of other base arms' rewards. The objective is to maximize the long-term average payoff, which is a linear function of the base arms' rewards and depends strongly on the network topology. To achieve this objective, we propose a policy that determines the causal relations by learning the network's topology and simultaneously exploits this knowledge to optimize the decision-making process. We establish a sublinear regret bound for the proposed algorithm. Numerical experiments using synthetic and real-world datasets demonstrate the superior performance of our proposed method compared to several benchmarks.