Saeed Ghoorchian
Quantum-Inspired Reinforcement Learning in the Presence of Epistemic Ambivalence
Mar 06, 2025Abstract:The complexity of online decision-making under uncertainty stems from the requirement of finding a balance between exploiting known strategies and exploring new possibilities. Naturally, the uncertainty type plays a crucial role in developing decision-making strategies that manage complexity effectively. In this paper, we focus on a specific form of uncertainty known as epistemic ambivalence (EA), which emerges from conflicting pieces of evidence or contradictory experiences. It creates a delicate interplay between uncertainty and confidence, distinguishing it from epistemic uncertainty that typically diminishes with new information. Indeed, ambivalence can persist even after additional knowledge is acquired. To address this phenomenon, we propose a novel framework, called the epistemically ambivalent Markov decision process (EA-MDP), aiming to understand and control EA in decision-making processes. This framework incorporates the concept of a quantum state from the quantum mechanics formalism, and its core is to assess the probability and reward of every possible outcome. We calculate the reward function using quantum measurement techniques and prove the existence of an optimal policy and an optimal value function in the EA-MDP framework. We also propose the EA-epsilon-greedy Q-learning algorithm. To evaluate the impact of EA on decision-making and the expedience of our framework, we study two distinct experimental setups, namely the two-state problem and the lattice problem. Our results show that using our methods, the agent converges to the optimal policy in the presence of EA.
Non-stationary Delayed Combinatorial Semi-Bandit with Causally Related Rewards
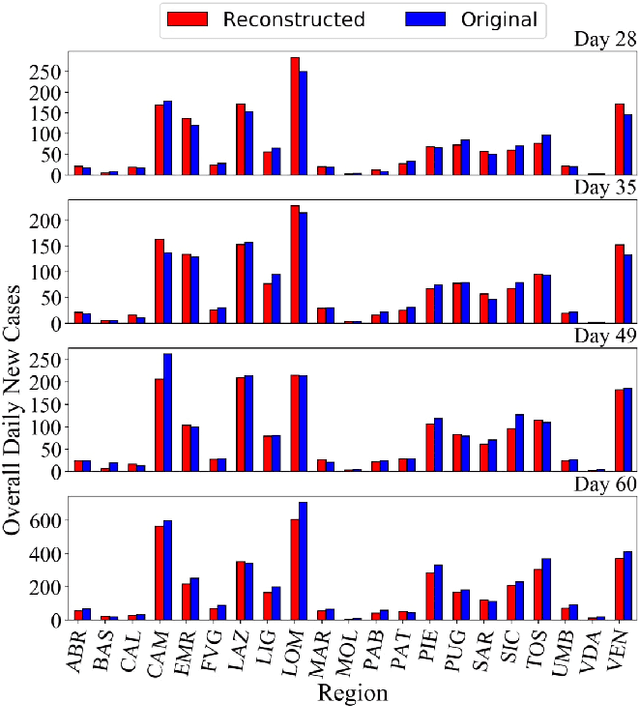
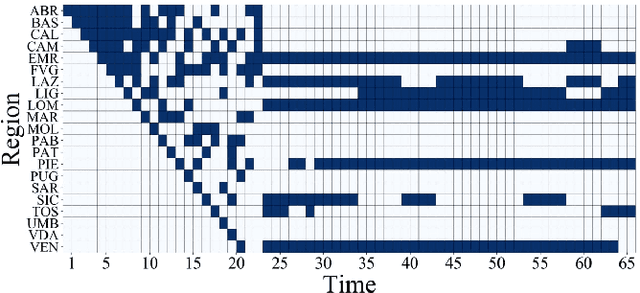
Jul 18, 2023Abstract:Sequential decision-making under uncertainty is often associated with long feedback delays. Such delays degrade the performance of the learning agent in identifying a subset of arms with the optimal collective reward in the long run. This problem becomes significantly challenging in a non-stationary environment with structural dependencies amongst the reward distributions associated with the arms. Therefore, besides adapting to delays and environmental changes, learning the causal relations alleviates the adverse effects of feedback delay on the decision-making process. We formalize the described setting as a non-stationary and delayed combinatorial semi-bandit problem with causally related rewards. We model the causal relations by a directed graph in a stationary structural equation model. The agent maximizes the long-term average payoff, defined as a linear function of the base arms' rewards. We develop a policy that learns the structural dependencies from delayed feedback and utilizes that to optimize the decision-making while adapting to drifts. We prove a regret bound for the performance of the proposed algorithm. Besides, we evaluate our method via numerical analysis using synthetic and real-world datasets to detect the regions that contribute the most to the spread of Covid-19 in Italy.
Online Learning with Costly Features in Non-stationary Environments
Jul 18, 2023Abstract:Maximizing long-term rewards is the primary goal in sequential decision-making problems. The majority of existing methods assume that side information is freely available, enabling the learning agent to observe all features' states before making a decision. In real-world problems, however, collecting beneficial information is often costly. That implies that, besides individual arms' reward, learning the observations of the features' states is essential to improve the decision-making strategy. The problem is aggravated in a non-stationary environment where reward and cost distributions undergo abrupt changes over time. To address the aforementioned dual learning problem, we extend the contextual bandit setting and allow the agent to observe subsets of features' states. The objective is to maximize the long-term average gain, which is the difference between the accumulated rewards and the paid costs on average. Therefore, the agent faces a trade-off between minimizing the cost of information acquisition and possibly improving the decision-making process using the obtained information. To this end, we develop an algorithm that guarantees a sublinear regret in time. Numerical results demonstrate the superiority of our proposed policy in a real-world scenario.
Linear Combinatorial Semi-Bandit with Causally Related Rewards
Dec 25, 2022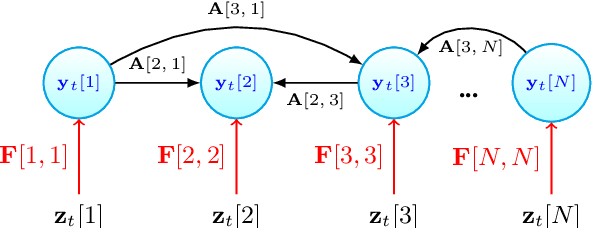
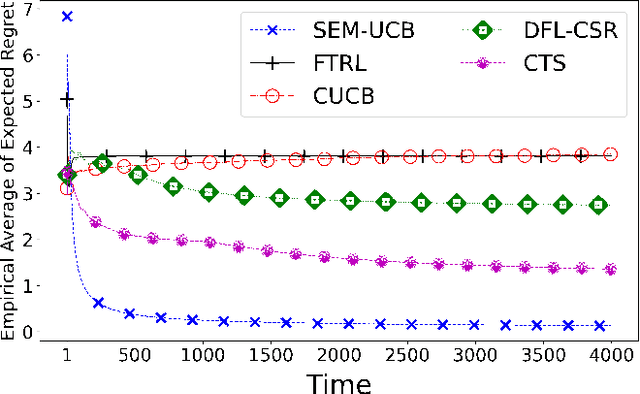
Abstract:In a sequential decision-making problem, having a structural dependency amongst the reward distributions associated with the arms makes it challenging to identify a subset of alternatives that guarantees the optimal collective outcome. Thus, besides individual actions' reward, learning the causal relations is essential to improve the decision-making strategy. To solve the two-fold learning problem described above, we develop the 'combinatorial semi-bandit framework with causally related rewards', where we model the causal relations by a directed graph in a stationary structural equation model. The nodal observation in the graph signal comprises the corresponding base arm's instantaneous reward and an additional term resulting from the causal influences of other base arms' rewards. The objective is to maximize the long-term average payoff, which is a linear function of the base arms' rewards and depends strongly on the network topology. To achieve this objective, we propose a policy that determines the causal relations by learning the network's topology and simultaneously exploits this knowledge to optimize the decision-making process. We establish a sublinear regret bound for the proposed algorithm. Numerical experiments using synthetic and real-world datasets demonstrate the superior performance of our proposed method compared to several benchmarks.
Bayesian Linear Bandits for Large-Scale Recommender Systems
Feb 07, 2022
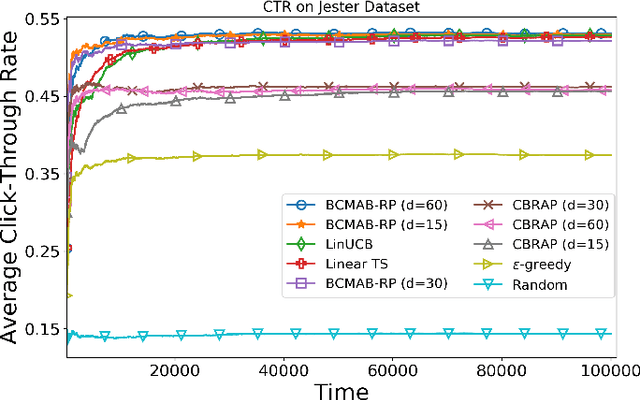

Abstract:Potentially, taking advantage of available side information boosts the performance of recommender systems; nevertheless, with the rise of big data, the side information has often several dimensions. Hence, it is imperative to develop decision-making algorithms that can cope with such a high-dimensional context in real-time. That is especially challenging when the decision-maker has a variety of items to recommend. In this paper, we build upon the linear contextual multi-armed bandit framework to address this problem. We develop a decision-making policy for a linear bandit problem with high-dimensional context vectors and several arms. Our policy employs Thompson sampling and feeds it with reduced context vectors, where the dimensionality reduction follows by random projection. Our proposed recommender system follows this policy to learn online the item preferences of users while keeping its runtime as low as possible. We prove a regret bound that scales as a factor of the reduced dimension instead of the original one. For numerical evaluation, we use our algorithm to build a recommender system and apply it to real-world datasets. The theoretical and numerical results demonstrate the effectiveness of our proposed algorithm compared to the state-of-the-art in terms of computational complexity and regret performance.
Multi-Armed Bandit for Energy-Efficient and Delay-Sensitive Edge Computing in Dynamic Networks with Uncertainty
Apr 12, 2019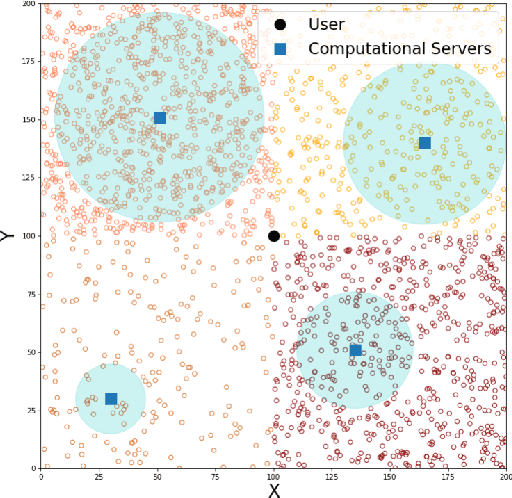
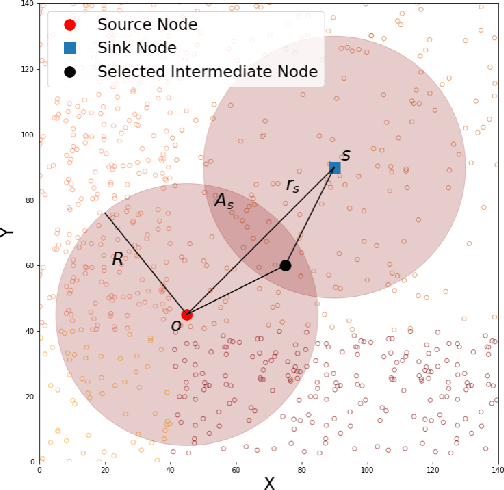
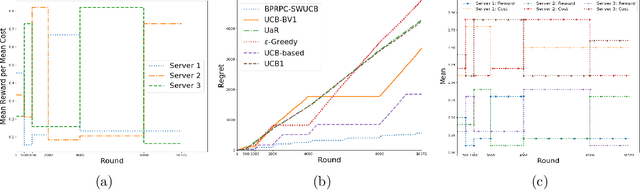
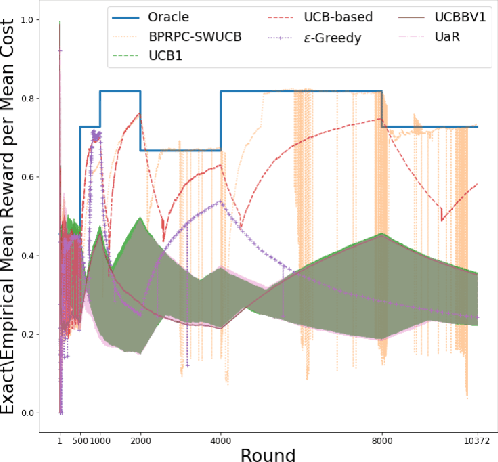
Abstract:In the emerging edge-computing paradigm, mobile devices offload the computational tasks to an edge server by routing the required data over the wireless network. The full potential of edge-computing becomes realized only if the devices select the most appropriate server in terms of the latency and energy consumption, among many available ones. This problem is, however, challenging due to the randomness of the environment and lack of prior information about the environment. Therefore, a smart device, which sequentially chooses a server under uncertainty, attempts to improve its decision based on the historical time- and energy consumption. The problem becomes more complicated in a dynamic environment, where key variables might undergo abrupt changes. To deal with the aforementioned problem, we first analyze the required time and energy to data transmission and processing. We then use the analysis to cast the problem as a budget-constrained multi-armed bandit problem, where each arm is associated with a reward and cost, with time-variant statistical characteristics. We propose a policy to solve the formulated bandit problem and prove a regret bound. The numerical results demonstrate the superiority of the proposed method compared to a number of existing solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge