Olivier Cappe
CNRS, DI-ENS, PSL
Regret Analysis of the Stochastic Direct Search Method for Blind Resource Allocation
Oct 11, 2022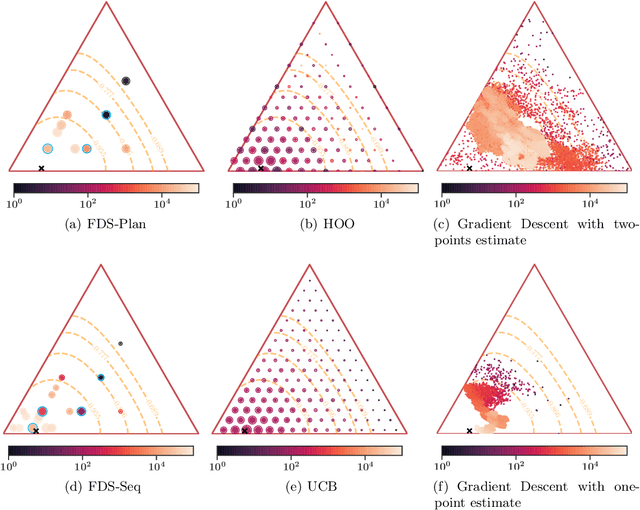
Abstract:Motivated by programmatic advertising optimization, we consider the task of sequentially allocating budget across a set of resources. At every time step, a feasible allocation is chosen and only a corresponding random return is observed. The goal is to maximize the cumulative expected sum of returns. This is a realistic model for budget allocation across subdivisions of marketing campaigns, when the objective is to maximize the number of conversions. We study direct search (aka pattern search) methods for linearly constrained and derivative-free optimization in the presence of noise. Those algorithms are easy to implement and particularly suited to constrained optimization. They have not yet been analyzed from the perspective of cumulative regret. We provide a regret upper-bound of the order of T 2/3 in the general case. Our mathematical analysis also establishes, as a by-product, time-independent regret bounds in the deterministic, unconstrained case. We also propose an improved version of the method relying on sequential tests to accelerate the identification of descent directions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge