Multitask Online Learning: Listen to the Neighborhood Buzz

We study multitask online learning in a setting where agents can only exchange information with their neighbors on an arbitrary communication network. We introduce $\texttt{MT-CO}_2\texttt{OL}$, a decentralized algorithm for this setting whose regret depends on the interplay between the task similarities and the network structure. Our analysis shows that the regret of $\texttt{MT-CO}_2\texttt{OL}$ is never worse (up to constants) than the bound obtained when agents do not share information. On the other hand, our bounds significantly improve when neighboring agents operate on similar tasks. In addition, we prove that our algorithm can be made differentially private with a negligible impact on the regret when the losses are linear. Finally, we provide experimental support for our theory.

Regret Analysis of the Stochastic Direct Search Method for Blind Resource Allocation

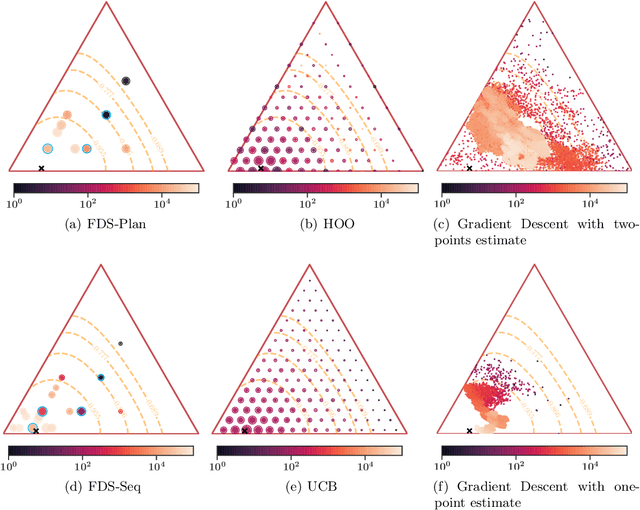
Motivated by programmatic advertising optimization, we consider the task of sequentially allocating budget across a set of resources. At every time step, a feasible allocation is chosen and only a corresponding random return is observed. The goal is to maximize the cumulative expected sum of returns. This is a realistic model for budget allocation across subdivisions of marketing campaigns, when the objective is to maximize the number of conversions. We study direct search (aka pattern search) methods for linearly constrained and derivative-free optimization in the presence of noise. Those algorithms are easy to implement and particularly suited to constrained optimization. They have not yet been analyzed from the perspective of cumulative regret. We provide a regret upper-bound of the order of T 2/3 in the general case. Our mathematical analysis also establishes, as a by-product, time-independent regret bounds in the deterministic, unconstrained case. We also propose an improved version of the method relying on sequential tests to accelerate the identification of descent directions.

Fast Rate Learning in Stochastic First Price Bidding

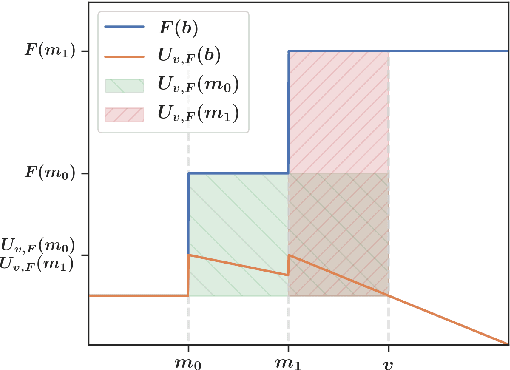
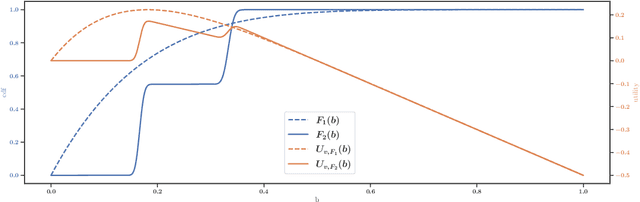
First-price auctions have largely replaced traditional bidding approaches based on Vickrey auctions in programmatic advertising. As far as learning is concerned, first-price auctions are more challenging because the optimal bidding strategy does not only depend on the value of the item but also requires some knowledge of the other bids. They have already given rise to several works in sequential learning, many of which consider models for which the value of the buyer or the opponents' maximal bid is chosen in an adversarial manner. Even in the simplest settings, this gives rise to algorithms whose regret grows as $\sqrt{T}$ with respect to the time horizon $T$. Focusing on the case where the buyer plays against a stationary stochastic environment, we show how to achieve significantly lower regret: when the opponents' maximal bid distribution is known we provide an algorithm whose regret can be as low as $\log^2(T)$; in the case where the distribution must be learnt sequentially, a generalization of this algorithm can achieve $T^{1/3+ \epsilon}$ regret, for any $\epsilon>0$. To obtain these results, we introduce two novel ideas that can be of interest in their own right. First, by transposing results obtained in the posted price setting, we provide conditions under which the first-price biding utility is locally quadratic around its optimum. Second, we leverage the observation that, on small sub-intervals, the concentration of the variations of the empirical distribution function may be controlled more accurately than by using the classical Dvoretzky-Kiefer-Wolfowitz inequality. Numerical simulations confirm that our algorithms converge much faster than alternatives proposed in the literature for various bid distributions, including for bids collected on an actual programmatic advertising platform.

Efficient Algorithms for Stochastic Repeated Second-price Auctions

Developing efficient sequential bidding strategies for repeated auctions is an important practical challenge in various marketing tasks. In this setting, the bidding agent obtains information, on both the value of the item at sale and the behavior of the other bidders, only when she wins the auction. Standard bandit theory does not apply to this problem due to the presence of action-dependent censoring. In this work, we consider second-price auctions and propose novel, efficient UCB-like algorithms for this task. These algorithms are analyzed in the stochastic setting, assuming regularity of the distribution of the opponents' bids. We provide regret upper bounds that quantify the improvement over the baseline algorithm proposed in the literature. The improvement is particularly significant in cases when the value of the auctioned item is low, yielding a spectacular reduction in the order of the worst-case regret. We further provide the first parametric lower bound for this problem that applies to generic UCB-like strategies. As an alternative, we propose more explainable strategies which are reminiscent of the Explore Then Commit bandit algorithm. We provide a critical analysis of this class of strategies, showing both important advantages and limitations. In particular, we provide a minimax lower bound and propose a nearly minimax-optimal instance of this class.